高考数学中的恒成立问题与存在性问题 4页

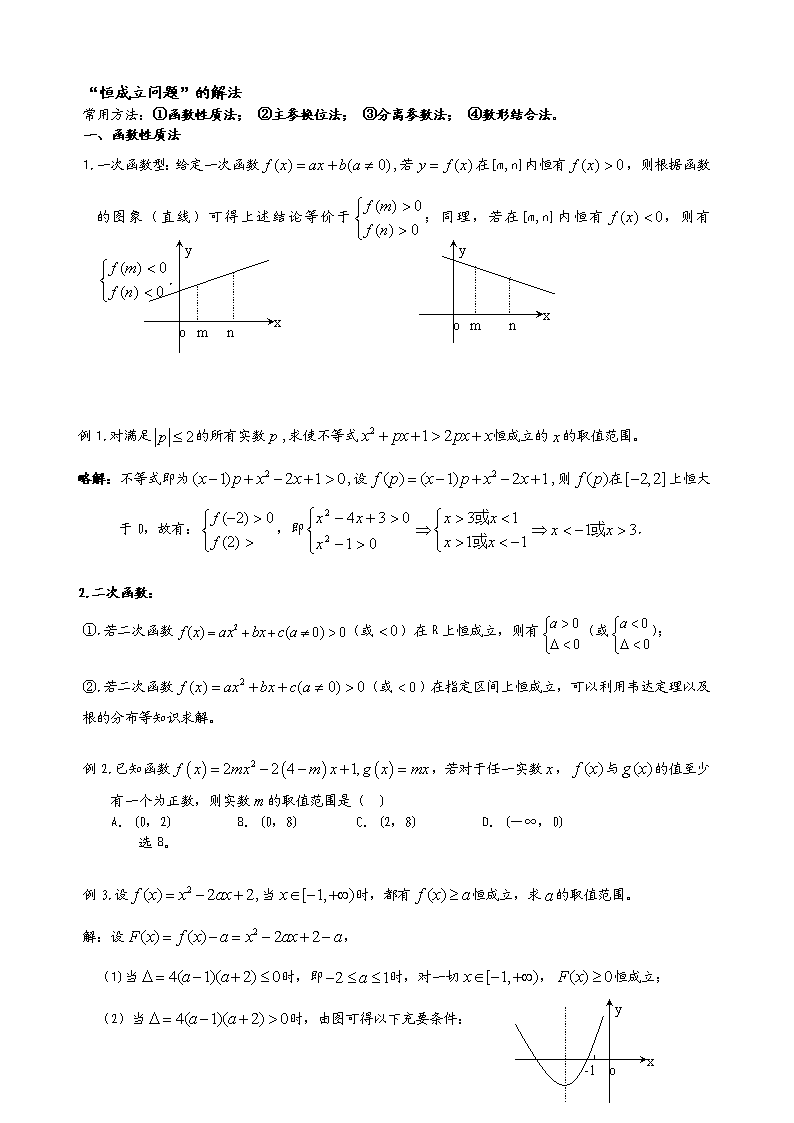
‎“恒成立问题”的解法 常用方法：①函数性质法； ②主参换位法； ③分离参数法； ④数形结合法。‎ 一、函数性质法 n m o x y n m o x y ‎1.一次函数型：给定一次函数,若在[m,n]内恒有，则根据函数的图象（直线）可得上述结论等价于；同理，若在[m,n]内恒有，则有.‎ 例1.对满足的所有实数,求使不等式恒成立的的取值范围。‎ 略解：不等式即为,设,则在上恒大于0，故有：，即.‎ ‎2.二次函数：‎ ①.若二次函数（或）在R上恒成立，则有（或）；‎ ②.若二次函数（或）在指定区间上恒成立，可以利用韦达定理以及根的分布等知识求解。‎ 例2.已知函数，若对于任一实数，与的值至少有一个为正数，则实数的取值范围是（ )‎ A．(0，2) B．(0，8) C．(2，8) D．(－∞，0)‎ 选B。‎ 例3.设,当时，都有恒成立，求的取值范围。‎ 解：设，‎ ‎（1)当时，即时，对一切，恒成立；‎ ‎-1‎ o x y ‎（2）当时，由图可得以下充要条件：‎ ‎ 即 ; 综合得的取值范围为[-3，1]。‎ 例4.关于的方程恒有解，求的范围。‎ 解法：设,则.则原方程有解即方程有正根。‎ ‎.‎ ‎3.其它函数：‎ 恒成立（若的最小值不存在，则恒成立的下界0）；‎ 恒成立（若的最大值不存在，则恒成立的上界0）.‎ 例5．设函数，其中常数，‎ ‎ （1）讨论的单调性；‎ ‎（2）若当时，恒成立，求的取值范围。.s.5.u.c.o.m ‎ 解：（2）由（I）知，当时，在或处取得最小值。‎ ‎；‎ 则由题意得 即 。‎ 二、主参换位法：某些含参不等式恒成立问题，在分离参数会遇到讨论的麻烦或者即使能容易分离出参数与变量，但函数的最值却难以求出时，可考虑把主元与参数换个位置，再结合其它知识，往往会取得出奇制胜的效果。‎ 例6．已知函数，其中为实数．‎ ‎（1）已知函数在处取得极值，求的值；‎ ‎（2）已知不等式对任意都成立，求实数的取值范围．‎ 解：由题设知“对都成立，即对都成立。设（），则是一个以为自变量的一次函数。恒成立，则对，为上的单调递增函数。 所以对，恒成立的充分必要条件是，，，于是的取值范围是。‎ 三、分离参数法：利用分离参数法来确定不等式（,为实参数）恒成立时参数的取值范围的基本步骤:‎ ‎（1） 将参数与变量分离，即化为（或）恒成立的形式；‎ ‎（2） 求在上的最大（或最小）值；‎ ‎（3） 解不等式(或) ，求得的取值范围。‎ 适用题型：（1）参数与变量能分离；（2）函数的最值易求出。‎ 例7．当时，恒成立，则的取值范围是 .‎ 解: 当时，由得.令，则易知在 上是减函数，所以，所以，∴.‎ 例8.已知时，不等式恒成立，求实数的取值范围。‎ 解：原不等式即为：，要使上式恒成立，只需-a+5大于的最大值，因为，‎ ‎∴，即或，解得a<8.‎ O 四、数形结合（对于型问题，利用数形结合思想转化为函数图象的关系再处理）：若把等式或不等式进行合理的变形后，能非常容易地画出等号或不等号两边函数的图象，则可以通过画图直接判断得出结果。尤其对于选择题、填空题这种方法更显方便、快捷。‎ 例9．若对任意,不等式恒成立，则实数的取值范围是（ ）‎ ‎(A) (B) (C) （D） ‎ ‎ 选B。‎ 例10.当)时， 恒成立，求a的取值范围。‎ 答案：.‎ x y o ‎1‎ ‎2‎ y1=(x-1)2‎ y2=logax 例11.已知关于x的方程有唯一解，求实数 ‎ 的取值范围。‎ 解：原问题即为：方程有唯一解。‎ 令，,则如图所示，要使和在轴上有 ‎ 唯一交点，则直线必须位于和之间。（包括但不包括)。‎ 当直线为时，;当直线为时，，‎ ‎∴的范围为。‎ 另解：方程在方程上有唯一解有唯一解。‎ 五。根据函数的奇偶性、周期性等性质：函数是奇偶性、单调性、周期性都在给定区间上恒成立。‎ 例12.若为偶函数，求的值。‎ 解：由题得：对一切恒成立，‎ ‎ ‎ ‎ 对一切xR恒成立，只需也必须 ‎.（)‎