高考数列公式总结 2页

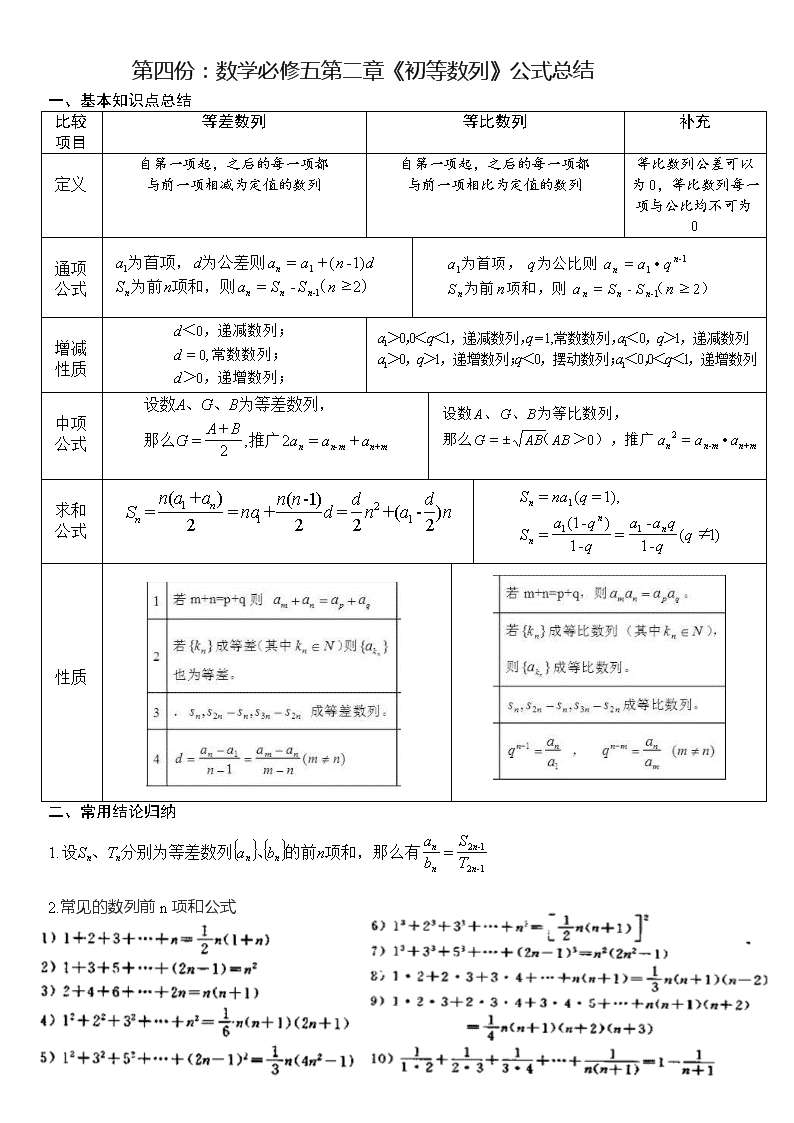
‎ 第四份：数学必修五第二章《初等数列》公式总结 一、基本知识点总结 比较项目 等差数列 等比数列 补充 定义 自第一项起，之后的每一项都 与前一项相减为定值的数列 自第一项起，之后的每一项都 与前一项相比为定值的数列 等比数列公差可以为0，等比数列每一项与公比均不可为0‎ 通项公式 增减性质 中项公式 求和公式 性质 二、 常用结论归纳 ‎1.‎ ‎2.常见的数列前n项和公式 3. 裂项相消法的运用公式：‎ 4. 构造法求数列通项公式（数量众多，此处仅为举例）‎ ‎(1)构造等比数列：形如的数列，可设，其中，那么是公比为q的等比数列；举例，，则，则为公比为2的等比数列.‎ ‎(2)构造等差数列：形如的数列，可以等式左右两边同时除以得，故，故数列是公差为q的等差数列.‎ ‎5.累加法与累乘法举例：‎ ‎（1）累加法：左边加左边，右边加右边，最后把左右相同部分消除.‎ 举例：已知数列满足，求数列的通项公式。‎ ‎（2）累乘法：每个是式子都写出来，全部乘起来，最后把相同的消除.‎ 举例：已知数列满足，求该数列通项公式 每个都写出来，依次乘起来得到：‎