高考文科数学试卷全国卷高考真题文科数学 16页

文科数学 2018年高三试卷 ‎ 文科数学 考试时间：____分钟 题型 单选题 填空题 简答题 总分 得分 ‎1.已知集合A={0，2}，B={ -2，-1，0，1，2}，则A∩B=‎ A. {0，2}‎ B. {1，2}‎ C. {0}‎ D. {-2，-1，0，1，2}‎ ‎2，设z=，则∣z∣=‎ A. 0‎ B. ‎ C. 1‎ D. ‎ ‎3.某地区经过一年的新农村建设，农村的经济收入增加了一倍，实现翻番，为更好地了解该地区农村的经济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例，得到如下饼图：‎ 则下面结论中不正确的是 A. 新农村建设后，种植收入减少 B. 新农村建设后，其他收入增加了一倍以上 C. 新农村建设后，养殖收入增加了一倍 D. 新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半 ‎4.已知椭圆C：+ =1的一个焦点为（2，0），则C的离心率为 A. ‎ B. ‎ C. ‎ D. ‎ ‎5.已知椭圆的上、下底面的中心分别为O₁，O₂，过直线的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为 A. 12π B. 12π C. 8π D. 10π ‎6.设函数f（x）=x ³+（a-1）x ²+ax。若f（x）为奇函数，则曲线y= f（x）在点（0，0）处的切线方程为 A. y=-2x B. y=-x C. y=2x D. y=x ‎7.在∆ABC中，AD为BC边上的中线，E为AD的中点，则=‎ A.  -‎ B. -‎ C. +‎ D. +‎ ‎8.已知函数f（x）=2cos ²x-sin ²x+2，则 A. f（x）的最小正周期为π，最大值为3‎ B. 不f（x）的最小正周期为π，最大值为4‎ C. f（x）的最小正周期为2π，最大值为3‎ D. D. 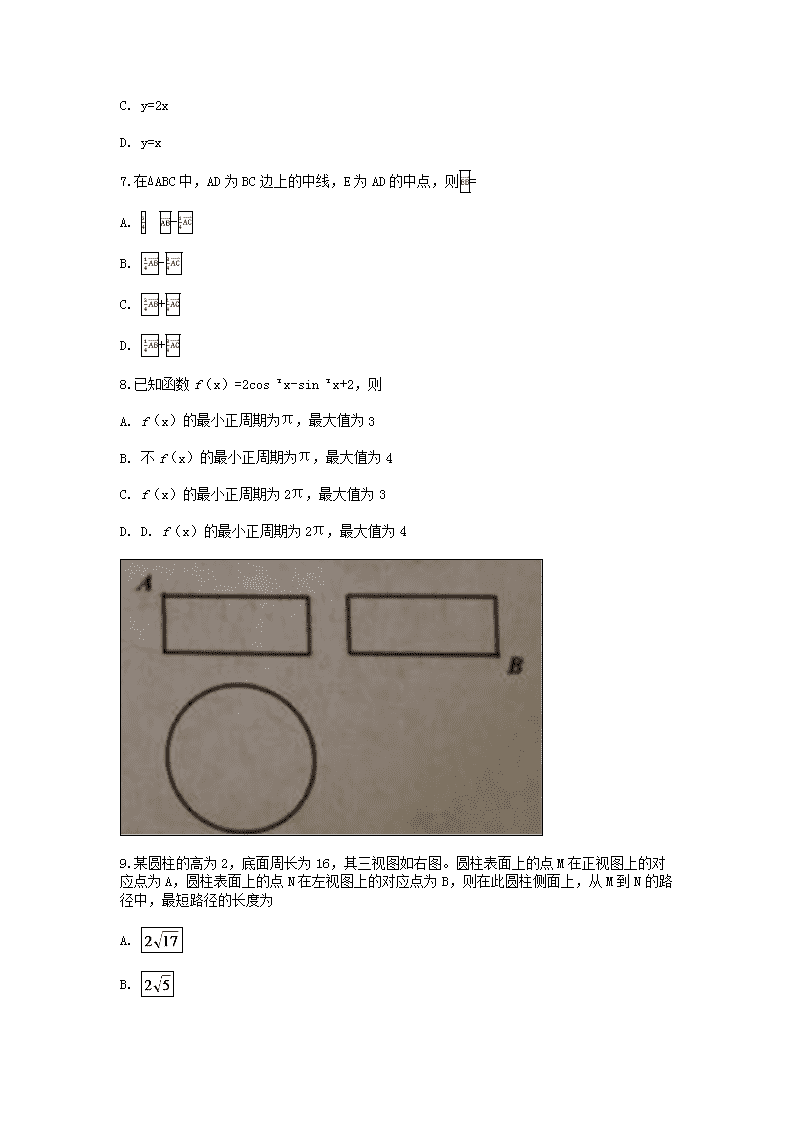f（x）的最小正周期为2π，最大值为4‎ ‎9.某圆柱的高为2，底面周长为16，其三视图如右图。圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为 A. ‎ B. ‎ C. 3‎ D. 2‎ ‎10.在长方体ABCD-A₁B₁C₁D₁中，AB=BC=2，AC ₁与平面BB1C1C所成的角为30°，则该长方体的体积为 A. 8‎ B. ‎ C. ‎ D. ‎ ‎11.已知角a的顶点为坐标原点，始边与x轴的非负半轴重合，终边上有两点A（1，a），B（2，b），且cos2a=，则=‎ A. ‎ B. ‎ C. ‎ D. 1‎ ‎12.设函数f（x）=则满足f（x+1）< f（2x）的x的取值范围是 A. （-∞，-1］‎ B. （0，+∞）‎ C. （-1，0）‎ D. （-∞，0）‎ 填空题 （本大题共4小题，每小题____分，共____分。） ‎ ‎13.已知函数f（x）= （x²+a），若f（3）=1，则a=____。‎ ‎14.若x，y满足约束条件则z=3x+2y的最大值为____。‎ ‎15.直线y=x+1与圆x²+y²+2y-3=0交于A，B两点，则∣AB∣=____。‎ ‎16. △ABC的内角A，B，C的对边分别为a，b，c，已知bsinC+csinB=4asinBsinC，b²+c²-a²=8，则△ABC的面积为____。‎ 简答题（综合题） （本大题共7小题，每小题____分，共____分。） ‎ ‎17.（12分）已知数列{}满足a₁=1，n =2（n+1），设。‎ ‎（1）求b₁，b₂，b₃；‎ ‎（2）判断数列{ }是否为等比数列，并说明理由。‎ ‎（3）求{}的通项公式。‎ ‎18.（12分）如图，在平行四边形ABCM中，AB=AC=3，∠ACM=90°，以AC为折痕将△ACM折起，使点M到达点D的位置，且AB⊥DA。‎ ‎（1）证明：平面ACD⊥平面ABC；‎ ‎（2）Q为线段AD上一点，P为线段BC上一点，且BP=DQ=DA，求三棱锥Q-ABP的体积。‎ ‎19.（12分）某家庭记录了未使用节水龙头50天的日用水量数据（单位：m³）和使用了节水龙头50天的日用水量数据，得到频数分布表如下：‎ 未使用节水龙头50天的日用水量频数分布表 使用了节水龙头50天的日用水量频数分布表 ‎（1）     在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图；‎ ‎（2）     估计该家庭使用节水龙头后，日用水量小于0.35 m³的概率；‎ ‎（3）     估计该家庭使用节水龙头后，一年能节省多少水？（一年按365天计算，同一组中的数据以这组数据所在区间中点的值作代表）‎ ‎20.（12分）‎ 设抛物线C：y ²=2x，点A（2，0），B（-2，0），过点A的直线l与C交于M，N两点，‎ ‎(1)当l与x轴垂直时，求直线BM的方程；‎ ‎(2)证明：∠ABM=∠ABM。‎ ‎21.（12分）‎ 已知函数f（x）=aex--1。‎ ‎（1）     设x=2是f（x）的极值点，求a，并求f（x）的单调区间；‎ ‎（2）     证明：当时，f（x）≥0。‎ ‎22.选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题计分。‎ ‎［选修4-4：坐标系与参数方程］（10分）‎ 在直角坐标系xOy中，曲线C ₁的方程为y=k+2，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C ₂的极坐标方程为p ²+2pcos θ-3=0。‎ ‎（1）     求C₂的直角坐标方程；‎ ‎（2）     若C₁与C₂有且仅有三个公共点，求C₁的方程。‎ ‎23.选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题计分。‎ ‎［选修4-5：不等式选讲］（10分）‎ 已知f（x）=∣x+1∣-∣ax-1∣。‎ ‎（1）当a=1时，求不等式f（x）>1的解集；‎ ‎（2）若x∈（0，1）时不等式是f（x）>x成立，求a的取得范围。‎ 答案 单选题 ‎ ‎1.  A 2.  C 3.  A 4.  C 5.  B 6.  D 7.  A 8.  B 9.  B 10.  C 11.  B 12.  D ‎ 填空题 ‎ ‎13.  ‎ ‎-7‎ ‎14.  ‎ ‎6‎ ‎15.  ‎ ‎16.  ‎ 简答题 ‎ ‎17.  ‎ ‎18.  ‎ ‎19.  ‎ ‎20.  ‎ ‎21.  ‎ ‎22.  ‎ ‎23.  ‎ 解析 单选题 ‎ 略  略  略  略  略  略  略  略  略  略  略  略  ‎ 填空题 ‎ 略  略  略  略  ‎ 简答题 ‎ 略  略  略  略  略  略  略  ‎