高考试题的探究一鳖臑几何体的试题赏析与探究文章修改稿 8页

鳖臑几何体的试题赏析与探究 岳 峻1 阮艳艳2 ‎ 安徽省太和县太和中学 236600‎ ‎2015年湖北高考数学之后，广大考生感言：阳马、鳖臑，想说爱你不容易；中学教师考后反思：阳马、鳖臑，不说爱你又没道理；试题评价专家说：湖北高考数学试题注重数学本质，突出数学素养，彰显数学文化.‎ 阳马、鳖臑是什么呢？‎ ‎1 试题再现 图 1‎ ‎1.1 文科试题 ‎《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑. 在如图1所示的阳马中，侧棱底面,且,点是的中点，连接．‎ ‎(I)证明：平面. 试判断四面体是否为鳖臑，若是，写出其每个面的直角（只需写出结论）；若不是，请说明理由；‎ ‎(II)记阳马的体积为，四面体的体积为，求的值．‎ 图2‎ ‎1.2 理科试题 ‎《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．如图2，在阳马中，侧棱底面，且，过棱的中点，作交于点，连接 ‎ ‎(I)证明：平面．试判断四面体是否为鳖臑，若是，写出其每个面的直角（只需写出结论）；若不是，说明理由；‎ ‎(II)若面与面所成二面角的大小为，求的值．‎ ‎2 鳖臑的史料 ‎2.1 史料 ‎《九章算术·商功》：“斜解立方，得两堑堵。斜解堑堵，其一为阳马，一为鳖臑。阳马居二，鳖臑居一，不易之率也。合两鳖臑三而一，验之以棊，其形露矣．”‎ 刘徽注：“此术臑者，背节也，或曰半阳马，其形有似鳖肘，故以名云。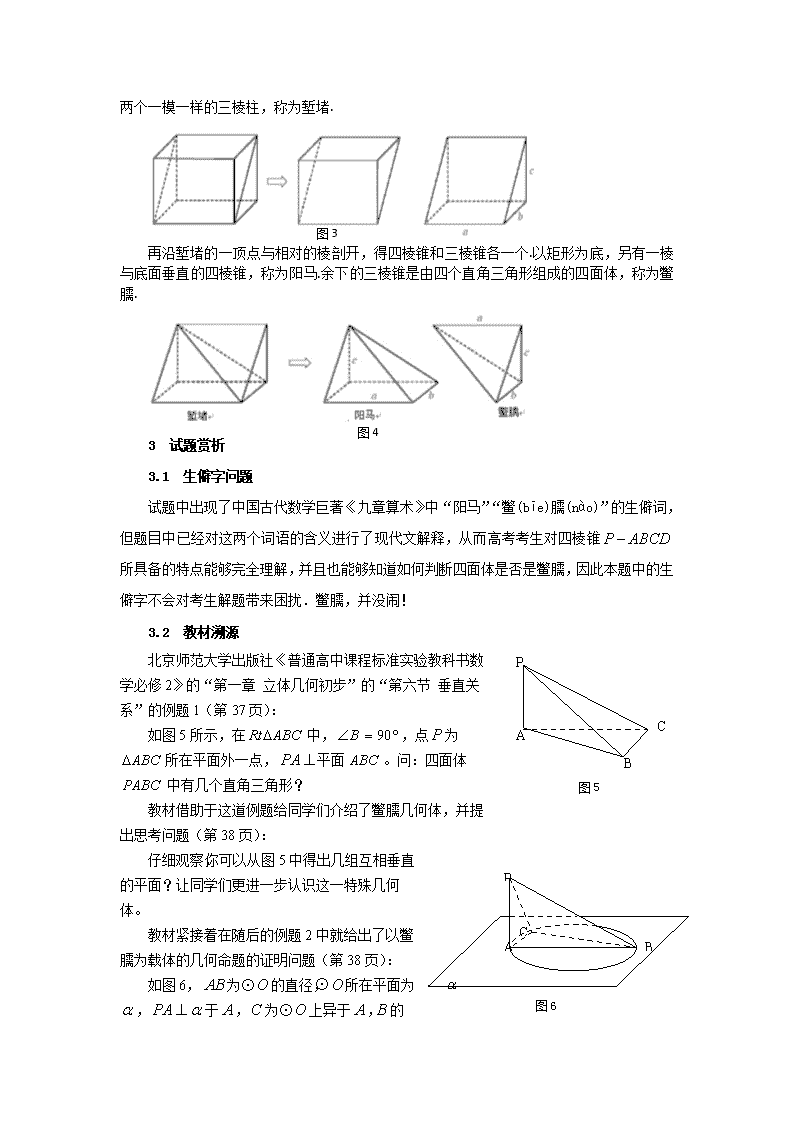中破阳马，得两鳖臑，鳖臑之起数，数同而实据半，故云六而一即得．”‎ ‎2.2 阐释 阳马和鳖臑是我国古代对一些特殊锥体的称谓，取一长方体，按下图斜割一分为二，得两个一模一样的三棱柱，称为堑堵.‎ 图3‎ 再沿堑堵的一顶点与相对的棱剖开，得四棱锥和三棱锥各一个.以矩形为底，另有一棱与底面垂直的四棱锥，称为阳马.余下的三棱锥是由四个直角三角形组成的四面体，称为鳖臑.‎ 图4‎ ‎3 试题赏析 ‎3.1 生僻字问题 试题中出现了中国古代数学巨著《九章算术》中“阳马”“鳖(bīe)臑(nào)”的生僻词，但题目中已经对这两个词语的含义进行了现代文解释，从而高考考生对四棱锥所具备的特点能够完全理解，并且也能够知道如何判断四面体是否是鳖臑，因此本题中的生僻字不会对考生解题带来困扰．鳖臑，并没闹！‎ ‎3.2 教材溯源 P A C B 图5‎ 北京师范大学出版社《普通高中课程标准实验教科书数学必修2》的“第一章 立体几何初步”的“第六节 垂直关系”的例题1（第37页）：‎ 如图5所示，在中，，点为所在平面外一点，平面。问：四面体中有几个直角三角形？‎ 教材借助于这道例题给同学们介绍了鳖臑几何体，并提出思考问题（第38页）：‎ P C A B 图6‎ 仔细观察，你可以从图5中得出几组互相垂直的平面？让同学们更进一步认识这一特殊几何体。‎ 教材紧接着在随后的例题2中就给出了以鳖臑为载体的几何命题的证明问题（第38页）：‎ 如图6，为⊙的直径，⊙所在平面为，于，为⊙上异于，‎ 的一点。求证：平面平面。‎ 该题借助于鳖臑这一几何体中丰富的垂直关系，让学生来熟悉垂直中的判定定理以及性质定理的应用。‎ ‎3.3 设计理念 普通高中数学课程标准中指出：数学是人类文化的重要组成部分，数学课程应帮助学生了解数学在人类文明发展中的作用，逐步形成正确的数学观。为此，高中数学教学应注重体现数学的文化价值，而2015年湖北卷就很恰当的体现了数学文化价值上的考查。命题者将题目的背景取自于古代数学典籍并不意味着试题的难度增大，匠心独运地体现了我国古代数学成果的灿烂辉煌，拓宽了知识面，考查考生的阅读能力、审题能力和应用能力，培养考生的创新精神，注重数学本质，提高数学素养，彰显命题组的博学与智慧．尤其是理科第19题、文科第20题，创新于数学史料的加工，以阳马和鳖臑为载体进行命题，来源于教材又囿于教材，彰显数学文化，数学味道正，文化气息浓，让“枯燥”的高考试卷多了几分生气和灵性，给人耳目一新的感觉．‎ ‎4 鳖臑几何体的性质的探究 图7‎ ‎4.1 鳖臑几何体中的垂直关系 如图7，鳖臑几何体中，平面，‎ ‎，于，于．‎ ‎（1）证明：；‎ ‎（2）证明：；‎ ‎（3）证明：；‎ ‎（4）证明：．‎ 证明 （1）因为平面，平面，所以，‎ 又，,所以；‎ ‎（2）因为，平面，所以，‎ 又，，所以平面，则，‎ 又，所以；‎ ‎（3）因为，所以．‎ ‎（4）因为，所以平面平面，‎ 又，所以平面，则，‎ 又，所以，‎ 评注 图形中异面直线与的距离等于线段的长度；异面直线与的距离等于线段的长度；‎ ‎4.2 鳖臑几何体中的空间角 图8‎ 如图8，设为与斜线的夹角，为与斜线在底面的射影的夹角，为与底面所成的角，为二面角的平面角，为直线与平面所成的角，为直线与底面所成的角， 为直线与平面所成的角，则 ‎（1）；‎ ‎（2）；‎ ‎（3）；‎ ‎（4）；‎ ‎（5）.‎ 证明 （1）；‎ ‎（2）；‎ ‎（3）；‎ ‎（4）；‎ ‎（5）过作于，连接，则平面，，‎ ‎.‎ 评注 图形中二面角的平面角的大小等于，二面角的平面角的大小等于，二面角的平面角的大小等于；‎ 直线与平面所成的角为，直线与平面所成的角为，直线 与平面所成的角为，直线与平面所成的角为，直线与平面所成的角为.‎ ‎5 鳖臑几何体模型的应用 ‎5.1 2015湖北真题评析 图 9‎ 例1 （同1.1 文科试题）‎ 解析 （I）因为底面，所以，‎ 由底面为长方形，有，‎ 而，所以. ‎ 而平面，所以. ‎ 又因为，点是的中点，所以. ‎ 而，所以平面.‎ 由平面，平面，可知四面体的四个面都是直角三角形，即四面体是一个鳖臑，其四个面的直角分别是,,,.‎ ‎（II）因为底面，是阳马的高，‎ 又点是的中点，则点到底面的距离为的，‎ 图10‎ 由于，所以．‎ 例2 （同1.2 理科试题）‎ 解析 （I）同例1 证明平面.‎ 而平面，所以平面平面.‎ 而平面平面，，‎ 所以平面.‎ 由平面，平面，可知四面体的四个面都是直角三角形，即四面体是一个鳖臑，其四个面的直角分别为.‎ ‎（II）因为平面，底面，则平面与平面所成二面角的平面角即为与所成的角，‎ 不妨设，则，在中, ，故．‎ ‎5.2 鳖臑在手，横扫立体几何试题 鳖臑几何体不仅覆盖了立体几何中点、线、面的各种位置关系，以及各种空间角的计算，又突出了“垂直”这个横贯立体几何知识的“红线”，因此，鳖臑几何体 是探求空间中线线、线面、面面垂直关系的十分重要的基本图形，也是研究棱锥、棱台的基本模型。‎ 图11‎ 例3 已知在内，于，于，，，求证：在的平分线上（即）．‎ 解析 因为，由三垂线定理逆定理知：，‎ 因为，‎ 所以≌，则，‎ 又因为，‎ 所以，故．‎ 图12‎ 评注 经过一个角的顶点引这个角所在平面的斜线，如果斜线与这个角两边夹角相等，那么斜线在平面上的射影是这个角的平分线所在直线．本题图形中的三棱锥就是鳖臑几何体，显然，这个三棱锥中蕴含着棱锥、棱台的所有要素。‎ 例4 （2015新课标I）如图12，四边形为菱形，为与交点，平面.‎ ‎(1)证明：平面平面；‎ ‎(2)若，，三棱锥的体积为，求该三棱锥的侧面积.‎ 解析 (1)因为四边形为菱形，所以，又平面，所以几何体是鳖臑，由鳖臑几何体的垂直关系性质1可知平面,又平面，所以平面平面.‎ ‎(2) 因为，，，所以，‎ 因为三棱锥的体积为，所以鳖臑几何体的体积为.‎ 设,则,，，‎ 图13‎ 所以的体积为，所以，‎ 所以△的面积为，△的面积与△的面积均为.故三棱锥的侧面积为.‎ 例5 （2015新课标Ⅱ）如图13，长方体 中， ， ，，点，分别在上，，过点，的平面与此长方体的面相交，交线围成一个正方形．‎ 图14‎ Q ‎(I)在图中画出这个正方形（不必说出画法和理由）；‎ ‎(II)求直线与平面所成角的正弦值.‎ 解析 (I)交线围成的正方形如图14. ‎ ‎(II)如图14，作于,则，；‎ 因为四边形为正方形,所以，于是，所以.‎ 作于，连接，则三棱锥就是鳖臑几何体，其中就是与平面所成角，‎ 设由鳖臑几何体的性质，则，‎ 图15‎ 又，则，‎ 故与平面所成角的正弦值为.‎ 例6 （2015山东）如图15，在三棱台中，，，分别为，的中点．‎ ‎(1)求证：平面；‎ ‎(2)若平面，， ，，求平面与平面所成的角（锐角）的大小． ‎ 解析 (1)略.‎ ‎(2)由，分别为，的中点，所以∥，‎ 因为，所以，‎ 又平面，所以几何体是鳖臑几何体；‎ 假设平面与平面所成的角为，，则由鳖臑几何体的性质可知：，‎ 又，所以，故平面与平面 所成的角（锐角）为．‎ ‎6 结束语 除此之外，在2015年的高考题中还有很多以鳖臑这一几何体为背景的立体几何问题，限于篇幅，忍痛割爱，不再赘述。‎ 命题者之所以对鳖臑这一几何体如此青睐，正是因为鳖臑几何体中有着丰富的垂直关系，是讨论线线垂直、线面垂直、面面垂直以及三种垂直关系相互转化的非常好的载体；正是因为鳖臑几何体蕴含着棱锥、棱台的所有要素，可以破解立体几何千变万化的空间角；正是因为鳖臑几何体是涵盖了立体几何中最基本、最核心的知识点的模型，蕴含的基本关系揭示了立体几何的基本结构与本质规律．‎ 鳖臑，是立体几何的灵魂．‎