高考数学理试题汇编立体几何 20页

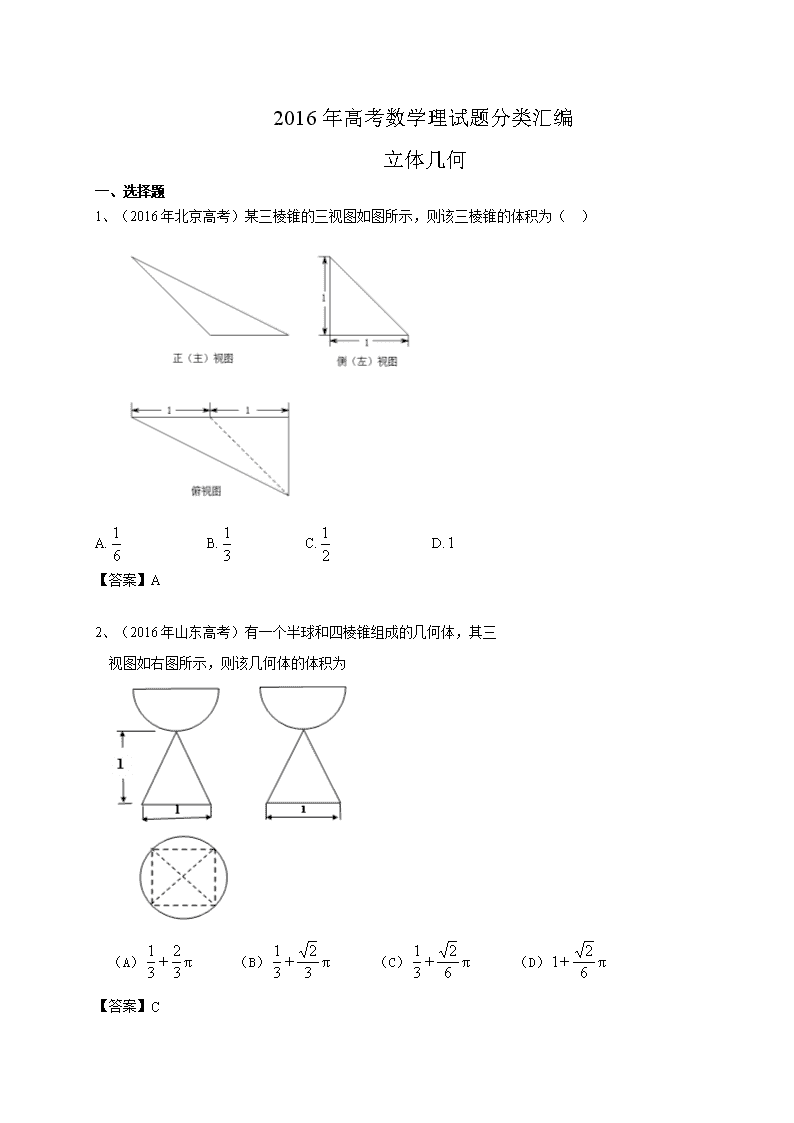
‎2016年高考数学理试题分类汇编 立体几何 一、选择题 ‎1、（2016年北京高考）某三棱锥的三视图如图所示，则该三棱锥的体积为（ ）‎ A. ‎ B. C. 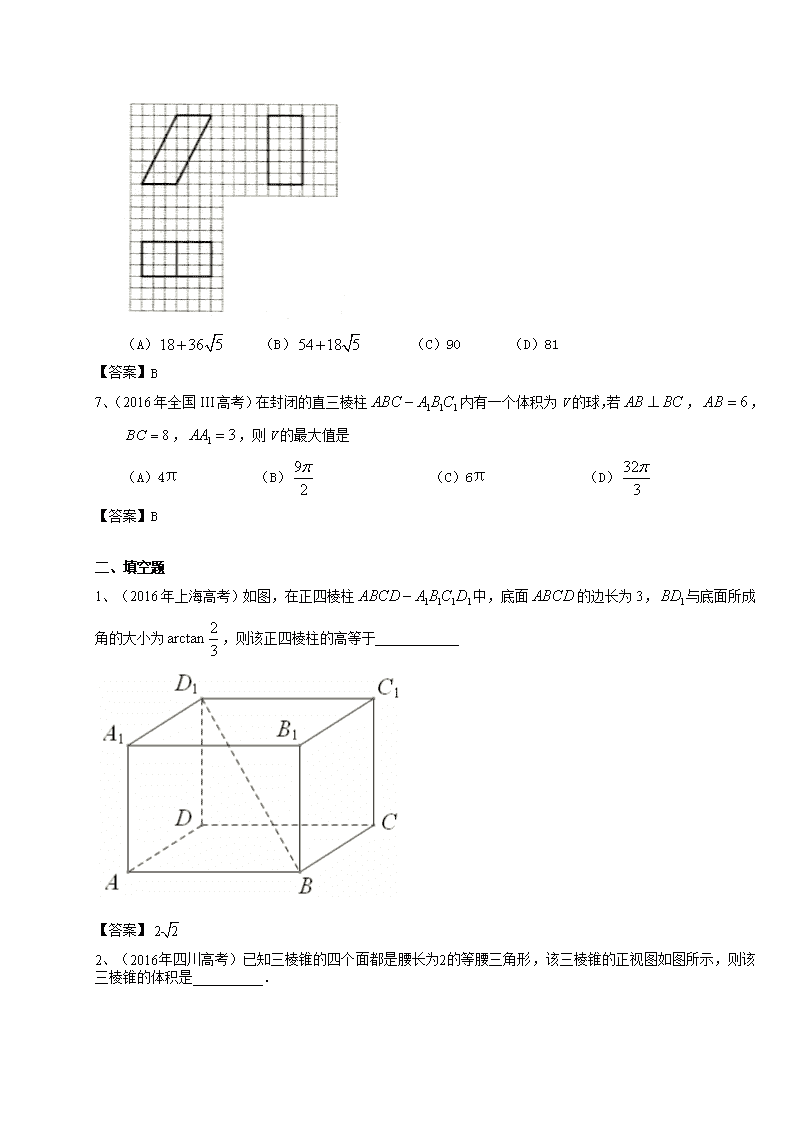D.‎ ‎【答案】A ‎2、（2016年山东高考）有一个半球和四棱锥组成的几何体，其三 视图如右图所示，则该几何体的体积为 ‎ （A） （B） （C） （D）‎ ‎【答案】C ‎3、（2016年全国I高考）如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是，则它的表面积是 ‎（A）17π （B）18π （C）20π （D）28π ‎ ‎ 【答案】A ‎ ‎4、（2016年全国I高考）平面过正方体ABCDA1B‎1C1D1的顶点A，//平面CB1D1，平面ABCD=m，平面ABB‎1 A1=n，则m，n所成角的正弦值为 ‎（A） （B） （C） （D）‎ ‎【答案】A ‎5、（2016年全国II高考）右图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为 ‎（A）20π （B）24π （C）28π （D）32π ‎【答案】C ‎6、（2016年全国III高考）如图，网格纸上小正方形的边长为1，粗实现画出的是某多面体的三视图，则该多面体的表面积为 ‎（A） （B） （C）90 （D）81‎ ‎【答案】B ‎7、（2016年全国III高考）在封闭的直三棱柱内有一个体积为V的球，若，，，，则V的最大值是 ‎（A）4π （B） （C）6π （D） ‎ ‎【答案】B 二、填空题 ‎1、（2016年上海高考）如图，在正四棱柱中，底面的边长为3，与底面所成角的大小为，则该正四棱柱的高等于____________‎ ‎【答案】‎ ‎2、（2016年四川高考）已知三棱锥的四个面都是腰长为2的等腰三角形，该三棱锥的正视图如图所示，则该三棱锥的体积是__________．‎ ‎【答案】‎ ‎3、（2016年天津高考）已知一个四棱锥的底面是平行四边形，该四棱锥的三视图如图所示（单位：m），则该四棱锥的体积为_______m3.‎ ‎【答案】2‎ ‎4、（2016年全国II高考） 是两个平面，是两条直线，有下列四个命题：‎ ‎（1）如果，那么.[‎ ‎（2）如果，那么.‎ ‎（3）如果，那么.‎ ‎（4）如果，那么与所成的角和与所成的角相等.‎ 其中正确的命题有 ．.(填写所有正确命题的编号）‎ ‎【答案】②③④‎ ‎5、（2016年浙江高考）某几何体的三视图如图所示（单位：cm），则该几何体的表面积是 cm2，体积是 cm3.‎ ‎【答案】 ‎ ‎6、（2016年浙江高考）如图，在△ABC中，AB=BC=2，∠ABC=120°.若平面ABC外的点P和线段AC上的点D，满足PD=DA，PB=BA，则四面体PBCD的体积的最大值是 .‎ ‎【答案】‎ 三、解答题 ‎1、（2016年北京高考） 如图，在四棱锥中，平面平面，，，，‎ ‎，，.‎ ‎（1）求证：平面； ‎ ‎（2）求直线与平面所成角的正弦值；‎ ‎（3）在棱上是否存在点，使得平面？若存在，求的值；若不存在，说明理由.‎ ‎【解】⑴∵面面 面面 ‎∵，面 ‎∴面 ‎∵面 ‎∴‎ 又 ‎∴面 ‎⑵取中点为，连结，‎ ‎∵‎ ‎∴‎ ‎∵‎ ‎∴‎ 以为原点，如图建系 易知，，，，‎ 则，，，‎ 设为面的法向量，令 ‎，则与面夹角有 ‎⑶假设存在点使得面 设，‎ 由（2）知，，，，‎ 有 ‎∴‎ ‎∵面，为的法向量 ‎∴‎ 即 ‎∴‎ ‎∴综上，存在点，即当时，点即为所求.‎ ‎2、（2016年山东高考）在如图所示的圆台中，AC是下底面圆O的直径，EF是上底面圆O的直径，FB是圆台的一条母线.‎ ‎（I）已知G,H分别为EC，FB的中点，求证：GH∥平面ABC；‎ ‎（II）已知EF=FB=AC=，AB=BC.求二面角的余弦值.‎ ‎【解】(Ⅰ)连结，取的中点，连结， ‎ ‎ 因为，在上底面内，不在上底面内，‎ E F B A C G H 所以上底面，所以平面； ‎ 又因为，平面，‎ 平面，‎ 所以平面；‎ ‎ 所以平面平面，‎ E F B A C O，‎ O x y z ‎ 由平面，所以平面．‎ ‎(Ⅱ) 连结， ‎ 以为原点，分别以为轴，‎ 建立空间直角坐标系．‎ ‎，‎ ‎，‎ 于是有，，，，‎ 可得平面中的向量，,‎ 于是得平面的一个法向量为，‎ 又平面的一个法向量为，‎ 设二面角为，‎ 则．‎ 二面角的余弦值为．‎ ‎3、（2016年上海高考）将边长为1的正方形（及其内部）绕的旋转一周形成圆柱，如图，长为，长为，其中与在平面的同侧。‎ ‎（1）求三棱锥的体积；‎ ‎（2）求异面直线与所成的角的大小。‎ ‎【解析】‎ 试题分析：（1）由题意可知，圆柱的高，底面半径．‎ 确定．计算后即得.‎ ‎（2）设过点的母线与下底面交于点，根据，知或其补角为直线与所成的角．确定，．得出．‎ 试题解析：（1）由题意可知，圆柱的高，底面半径．‎ 由的长为，可知．‎ ‎，‎ ‎．‎ ‎（2）设过点的母线与下底面交于点，则，‎ 所以或其补角为直线与所成的角．‎ 由长为，可知，‎ 又，所以，‎ 从而为等边三角形，得．‎ 因为平面，所以．‎ 在中，因为，，，所以，‎ 从而直线与所成的角的大小为．‎ ‎4、（2016年四川高考）如图，在四棱锥中，，，，E为棱AD的中点，异面直线PA与CD所成的角为.‎ ‎（I）在平面PAB内找一点M，使得直线平面PBE，‎ 并说明理由；‎ ‎（II）若二面角的大小为，求直线PA与 平面PCE所成角的正弦值.‎ ‎【解】（I）延长，交直线于点，‎ ‎ ∵为中点，‎ ‎ ∴，‎ ‎ ∵，‎ ‎ ∴，‎ ‎ ∵ 即 ，‎ ‎ ∴四边形为平行四边形，，‎ ‎ ∵，‎ ‎ ∴，‎ ‎ ∴，‎ ‎ ∵面，‎ ‎ ∴面，‎ ‎ ∵，面，‎ ‎ ∴面 故在面上可找到一点使得面.‎ ‎（II）过作交于点，连结，过作交于点，‎ ‎ ∵，与所成角为，‎ ‎ ∴，，‎ ‎ ∵，‎ ‎∴，‎ ‎∵面，‎ ‎∴，‎ ‎∵且，‎ ‎∴面，‎ ‎∵面，‎ ‎∴，‎ ‎∵且，‎ ‎∴面，‎ ‎∴为所求与面所成的角，‎ ‎∵面，即.‎ ‎∴为二面角所成的平面角,‎ 由题意可得，而,‎ ‎∴,‎ ‎∵,四边形是平行四边形，，‎ ‎∴四边形是正方形，‎ ‎∴，‎ ‎∴，‎ ‎ ∵，‎ ‎ ∴，‎ ‎ ∴，‎ ‎ ∴.‎ ‎5、（2016年天津高考）如图，正方形ABCD的中心为O，四边形OBEF为矩形，平面OBEF⊥平面ABCD，点G为AB的中点，AB=BE=2.‎ ‎（I）求证：EG∥平面ADF；‎ ‎（II）求二面角O-EF-C的正弦值；‎ ‎（III）设H为线段AF上的点，且AH=HF，求直线BH和平面CEF所成角的正弦值.‎ ‎【解析】（Ⅰ）证明：找到中点，连结，‎ ‎∵矩形,∴‎ ‎∵、是中点，∴是的中位线 ‎∴且 ‎∵是正方形中心 ‎∴‎ ‎∴且 ‎∴四边形是平行四边形 ‎∴‎ ‎∵面 ‎∴面 ‎（Ⅱ）正弦值 解：如图所示建立空间直角坐标系 ‎，，，‎ 设面的法向量 得：‎ ‎∴‎ ‎∵面，‎ ‎∴面的法向量 ‎（Ⅲ）∵‎ ‎∴‎ 设 ‎∴‎ 得：‎ ‎6、（2016年全国I高考）如图，在以A，B，C，D，E，F为顶点的五面体中，面ABEF为正方形，AF=2FD，，且二面角DAFE与二面角CBEF都是．‎ ‎（I）证明：平面ABEF平面EFDC；‎ ‎（II）求二面角EBCA的余弦值．‎ ‎【解析】‎ ⑴ ∵为正方形 ‎∴‎ ‎∵‎ ‎∴‎ ‎∵‎ ‎∴面 面 ‎∴平面平面 ⑵ 由⑴知 ‎∵‎ 平面 平面 ‎∴平面 平面 ‎∵面面 ‎∴,∴‎ ‎∴四边形为等腰梯形 以为原点，如图建立坐标系，设 ‎ ‎ ‎，，‎ 设面法向量为.‎ ‎，即 设面法向量为 ‎.即 设二面角的大小为.‎ 二面角的余弦值为 ‎7、（2016年全国II高考）如图，菱形的对角线与交于点，，点分别在上，，交于点．将沿折到位置，．‎ ‎（Ⅰ）证明：平面；‎ ‎（Ⅱ）求二面角的正弦值．‎ ‎【解析】⑴证明：∵，∴，‎ ‎∴．‎ ‎∵四边形为菱形，∴，‎ ‎∴，∴，∴．‎ ‎∵，∴；‎ 又，，∴，‎ ‎∴，‎ ‎∴，‎ ‎∴，‎ ‎∴．‎ 又∵，‎ ‎∴面．‎ ‎⑵建立如图坐标系．‎ ‎，，，，‎ ‎，，，‎ 设面法向量，‎ 由得，取，‎ ‎∴．‎ 同理可得面的法向量，‎ ‎∴，‎ ‎∴．‎ ‎8、（2016年全国III高考）如图，四棱锥中，地面，，，，为线段上一点，，为的中点．‎ ‎（I）证明平面；‎ ‎（II）求直线与平面所成角的正弦值.‎ 设为平面的法向量，则，即，可取，‎ 于是.‎ ‎9、（2016年浙江高考）如图,在三棱台中,平面平面 ‎,,BE=EF=FC=1,BC=2,AC=3.‎ ‎(I)求证：EF⊥平面ACFD；‎ ‎(II)求二面角B-AD-F的平面角的余弦值.‎ ‎（II）方法一：‎ 过点作，连结．‎ 因为平面，所以，则平面，所以．‎ 所以，是二面角的平面角．‎ 在中，，，得．‎ 在中，，，得．‎ 所以，二面角的平面角的余弦值为．‎ ‎ ‎ ‎10、(2016江苏省高考)如图，在直三棱柱ABC-A1B‎1C1中，D，E分别为AB，BC的中点，点F在侧棱B1B上，且 ， .‎ 求证：（1）直线DE∥平面A‎1C1F；‎ ‎（2）平面B1DE⊥平面A‎1C1F. ‎ 证明：（1）在直三棱柱中，‎ 在三角形ABC中，因为D,E分别为AB,BC的中点.‎ 所以，于是 又因为DE平面平面 所以直线DE//平面 ‎（2）在直三棱柱中，‎ 因为平面，所以 又因为 所以平面 因为平面，所以 又因为 所以 因为直线，所以