【物理】2020届一轮复习人教版第二章第二讲力的合成与分解学案 14页

第二讲 力的合成与分解 [小题快练] 1．判断题 (1)合力及其分力均为作用于同一物体上的力．( √ ) (2)合力及其分力可以同时作用在物体上．( × ) (3)几个力的共同作用效果可以用一个力来代替．( √ ) (4)在进行力的合成与分解时，都要应用平行四边形定则或三角形定则．( √ ) (5)两个力的合力一定比其分力大．( × ) (6)互成角度的两个力的合力与它的分力间一定构成封闭的三角形．( √ ) 2．(多选)两个共点力的合力为 F，如果它们之间的夹角θ固定不变，使其中一个力增大，则( BC ) A．合力 F 一定增大 B．合力 F 的大小可能不变 C．合力 F 可能增大，也可能减小 D．当 0°＜θ＜90°，合力 F 一定减小 3．(多选)两个共点力 F1、F2 大小不同，它们的合力大小为 F，则( AD ) A．F1、F2 同时增大一倍，F 也增大一倍 B．F1、F2 同时增加 10 N，F 也一定增加 10 N C．F1 增加 10 N，F2 减少 10 N，F 一定不变 D．若 F1、F2 中的一个增大，F 不一定增大 4．将物体所受重力按力的效果进行分解，下列图中错误的是( C ) 考点一 力的合成问题 (自主学习) 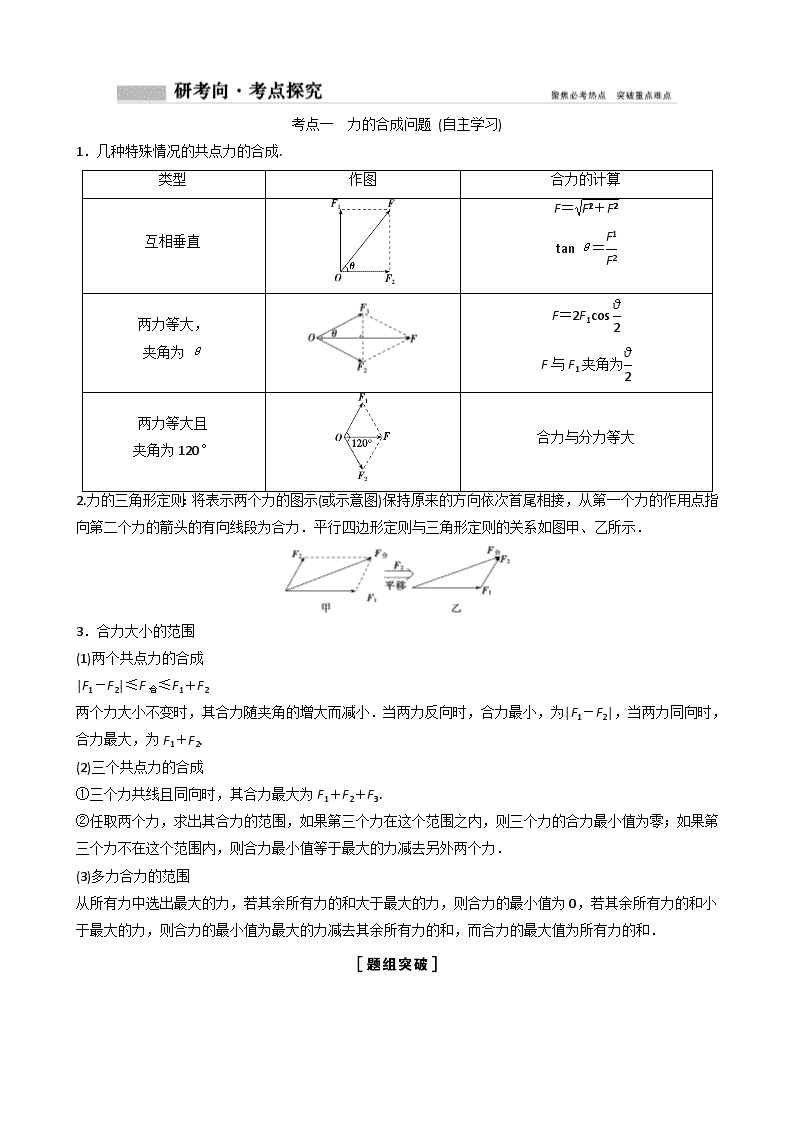1．几种特殊情况的共点力的合成. 类型 作图 合力的计算 互相垂直 F＝ F21＋F22 tan θ＝F1 F2 两力等大， 夹角为θ F＝2F1cos θ 2 F 与 F1 夹角为θ 2 两力等大且 夹角为 120° 合力与分力等大 2.力的三角形定则：将表示两个力的图示(或示意图)保持原来的方向依次首尾相接，从第一个力的作用点指 向第二个力的箭头的有向线段为合力．平行四边形定则与三角形定则的关系如图甲、乙所示． 3．合力大小的范围 (1)两个共点力的合成 |F1－F2|≤F 合≤F1＋F2 两个力大小不变时，其合力随夹角的增大而减小．当两力反向时，合力最小，为|F1－F2|，当两力同向时， 合力最大，为 F1＋F2. (2)三个共点力的合成 ①三个力共线且同向时，其合力最大为 F1＋F2＋F3. ②任取两个力，求出其合力的范围，如果第三个力在这个范围之内，则三个力的合力最小值为零；如果第 三个力不在这个范围内，则合力最小值等于最大的力减去另外两个力． (3)多力合力的范围 从所有力中选出最大的力，若其余所有力的和大于最大的力，则合力的最小值为 0，若其余所有力的和小 于最大的力，则合力的最小值为最大的力减去其余所有力的和，而合力的最大值为所有力的和． 1－1.[合力的求解] (2019·宁夏石嘴山三中月考)某物体在四个共点力作用下处于平衡状态，若 F4 的方向 沿逆时针方向转过 60°角，但其大小保持不变，其余三个力的大小和方向均保持不变，此时物体受到的合 力的大小为( ) A．0 B．F4 C. 2F4 D．2F4 解析：物体在四个共点力作用下处于平衡状态，即物体所受合外力为 0，把 F4 的方向沿逆时针转过 60°角 而大小保持不变，其余三个力的合力为－F4，则－F4 与旋转后的 F4 成 120°角，根据平行四边形定则：总 合力为 F4，故 B 正确． 答案：B 1－2. [合力与分力的关系] (2018·全国卷Ⅲ)如图，两个轻环 a 和 b 套在位于竖直面内的一段固定圆弧上； 一细线穿过两轻环，其两端各系一质量为 m 的小球．在 a 和 b 之间的细线上悬挂一小物块．平衡时，a、b 间的距离恰好等于圆弧的半径．不计所有摩擦．小物块的质量为( ) A.m 2 B． 3 2 m C．m D．2m 解析：如图所示，由于不计摩擦，线上张力处处相等，则轻环受细线的作用力的合力方向指向圆心．由于 a、b 间距等于圆弧半径，则∠aOb＝60°，进一步分析知，细线与 aO、bO 间的夹角皆为 30°.取悬挂的小 物块进行研究，悬挂小物块的细线张角为 120°，由平衡条件知，小物块的质量与小球的质量相等，即为 m.故 C 正确． 答案：C 考点二 力的分解问题 (师生共研) 力的分解常用的方法 正交分解法 效果分解法 分解 方法 将一个力沿着两个互相垂直的方向进 行分解的方法 根据一个力产生的实际效果进行分解 实例 分析 x 轴方向上的分力： Fx＝Fcos θ y 轴方向上的分力： Fy＝Fsin θ F1＝ G cos θ F2＝Gtan θ [典例] 如图，墙上有两个钉子 a 和 b，它们的连线与水平方向的夹角为 45°，两者的高度差为 l.一条不 可伸长的轻质细绳一端固定于 a 点，另一端跨过光滑钉子 b 悬挂一质量为 m1 的重物．在绳上距 a 端l 2 的 c 点有一固定绳圈．若绳圈上悬挂质量为 m2 的钩码，平衡后绳的 ac 段正好水平，则重物和钩码的质量比m1 m2 为( ) A. 5 B．2 C. 5 2 D． 2 解析：方法一 (力的效果分解法) 钩码的拉力 F 等于钩码重力 m2g，将 F 沿 ac 和 bc 方向分解，两个分力分别为 Fa、Fb，如图甲所示，其中 Fb＝m1g，由几何关系可得 cos θ＝ F Fb ＝m2g m1g ，又由几何关系得 cos θ＝ l l2＋l 2 2 ，联立解得m1 m2 ＝ 5 2 . 方法二 (正交分解法) 绳圈受到 Fa、Fb、F 三个力作用，如图乙所示，将 Fb 沿水平方向和竖直方向正交分 解，由竖直方向受力平衡得 m1gcos θ＝m2g；由几何关系得 cos θ＝ l l2＋l 2 2 ，联立解得m1 m2 ＝ 5 2 . 答案：C [反思总结] 力的分解问题的求解方法的选取原则 1．选用哪一种方法进行力的分解要视情况而定，一般来说，当物体受到三个或三个以下的力时，常利用 三角形法则或按实际效果进行分解，若这三个力中，有两个力互相垂直，可选用正交分解法． 2．当物体受到三个以上的力时，常用正交分解法． 2－1.[力的正交分解法] (2019·浙江台州中学统练)如图甲所示，将由两根短杆组成的一个自锁定起重吊 钩放入被吊的空罐内，使其张开一定的夹角压紧在罐壁上，其内部结构如图乙所示．当钢绳向上提起时， 两杆对罐壁越压越紧，当摩擦力足够大时，就能将重物提升起来，且罐越重，短杆提供的压力越大．若罐 的质量为 m，短杆与竖直方向的夹角θ＝60°，匀速吊起该罐时，短杆对罐壁的压力大小为 (短杆的质量 不计，重力加速度为 g) ( ) A．mg B． 3 2 mg C.1 2 mg D． 3mg 解析：先对罐整体受力分析，受重力和拉力，根据平衡条件，拉力等于重力，故：T＝mg；再将细线的拉 力沿着两个短杆方向分解，如图所示： 解得：T1＝T2＝ T 2 cos θ ＝mg，最后将短杆方向分力沿着水平和竖直方向正交分解，如图所示： T1x＝T1sin θ＝ 3 2 mg，根据牛顿第三定律可知故短杆对罐壁的压力为 3 2 mg，故选 B. 答案：B 2－2.[力的效果分解法] 如图所示，三根粗细均匀完全相同的圆木 A、B、C 堆放在水平地面上，处于静止 状态，每根圆木的质量为 m，截面的半径为 R，三个截面圆心连线构成的等腰三角形的顶角∠O1＝120°， 若在地面上的两根圆木刚好要滑动，设最大静摩擦力等于滑动摩擦力，不考虑圆木之间的摩擦，重力加速 度为 g，则( ) A．圆木间的弹力为 1 2 mg B．下面两根圆木对地面的压力均为 3 2 mg C．地面上的每根圆木受到地面的作用力为 3 2 mg D．地面与圆木间的动摩擦因数为 3 2 解析：对 A 进行受力分析，如图所示，A 处于平衡状态，合力为零，则有 N2cos θ 2 ＝1 2 mg，解得 N1＝N2＝ 1 2 mg cos 60° ＝mg，故 A 错误；对整体受力分析，受到重力、地面的支持力、B 受到的向右的摩擦力和 C 受到 的向左的摩擦力，由对称性可知，竖直方向有 NB＝NC＝3 2 mg，故 B 正确； 对 B 进行研究，地面对 B 的作用力等于地面对 B 的支持力与地面对 B 的摩擦力的合力 F＝ 3 2 mg2＋f2， 大于 3 2 mg，故 C 错误；对 C 进行研究，根据平衡条件得 f＝N2sin 60°＝mg× 3 2 ＝ 3 2 mg，所以地面对 C 的 摩擦力大小为 3 2 mg，根据摩擦力公式 f＝μNC，可得μ＝ f NC ＝ 3 2 mg 3 2 mg ＝ 3 3 ，故 D 错误． 答案：B 2－3.[两种方法的综合] 某压榨机的结构示意图如图所示，其中 B 为固定铰链，若在 A 铰链处作用一垂直 于墙壁的力 F，则由于力 F 的作用，使滑块 C 压紧物体 D，设 C 与 D 光滑接触，杆的重力及滑块 C 的重力 不计，图中 a＝0.5 m，b＝0.05 m，则物体 D 所受压力的大小与力 F 的比值为( ) A．4 B．5 C．10 D．1 解析：按力 F 的作用效果沿 AC、AB 杆方向分解为图甲所示的 F1、F2，则 F1＝F2＝ F 2cos θ ，由几何知识得 tan θ＝a b ＝10，再按 F1 的作用效果将 F1 沿水平向左和竖直向下分解为图乙所示的 F3、F4，则 F4 ＝F1 sin θ， 联立得 F4＝5F，即物体 D 所受压力的大小与力 F 的比值为 5，B 对． 答案：B 考点三 对称法解决非共面力问题 (自主学习) 在力的合成与分解的实际问题中，经常遇到物体受四个以上的非共面力作用处于平衡状态的情况，解决此 类问题时要注意图形结构的对称性特点，结构的对称性往往对应着物体受力的对称性，即某些力大小相等． 3－1.[大小相等的非共面力] 如图所示，一半圆形降落伞边缘用 24 根伞绳中心对称分布，下端悬挂一名飞 行员，每根绳与中轴线的夹角为 30°，飞行员及飞行员身上装备的总质量为 80 kg，降落伞的质量为 40 kg. 当匀速降落时，不计飞行员自身所受空气作用力，每根悬绳的拉力是( ) A．50 N B．100 3 N C.200 3 9 N D．100 3 3 N 解析：把绳的拉力正交分解为竖直向上和水平方向，竖直分力为 Fy＝Fcos 30°＝ 3 2 F，以飞行员为研究对 象，由平衡条件知，24Fy＝mg，其中 m 为飞行员及身上装备的总质量，解得：F＝200 3 9 N，故 C 正确． 答案：C 3－2.[大小不等的非共面力] (多选)(2017·广东卷)如图所示，三条绳子的一端都系在细直杆顶端，另一端 都固定在水平地面上，将杆竖直紧压在地面上，若三条绳长度不同．下列说法正确的有( ) A．三条绳中的张力都相等 B．杆对地面的压力大于自身重力 C．绳子对杆的拉力在水平方向的合力为零 D．绳子拉力的合力与杆的重力是一对平衡力 解析：杆静止在水平地面上，杆受到重力、三条绳子的拉力和地面对它的支持力共同作用．根据平衡条件， 三条绳的拉力的合力竖直向下，故绳子对杆的拉力在水平方向的合力为零．杆对地面的压力大小等于杆的 重力与三条绳的拉力的合力之和，选项 B、C 正确；由于三条绳长度不同，即三条绳与竖直方向的夹角不 同，所以三条绳上的张力不相等，A 错误；绳子拉力的合力与杆的重力方向相同，因此两者不是一对平衡 力，D 错误． 答案：BC 1．减速带是交叉路口常见的一种交通设施，车辆驶过减速带时要减速，以保障行人的安全．当汽车前轮 刚爬上减速带时，减速带对车轮的弹力为 F，下列关于弹力 F 画法正确且分解合理的是( B ) 2. 如图所示，某人静躺在椅子上，椅子的靠背与水平面之间有固定倾斜角θ.若此人所受重力为 G，则椅子 各部分对他的作用力的合力大小为( A ) A．G B．Gsin θ C．Gcos θ D．Gtan θ 3. 如图所示，起重机将重为 G 的重物匀速吊起，此时四条钢索与竖直方向的夹角均为 60°，则每根钢索 中弹力大小为( D ) A.G 4 B． 3G 6 C. 3G 4 D．G 2 4. (2018·广西高级中学月考)两个质量相同的直角楔形物体 a 和 b，分别在垂直于斜边的恒力 F1 和 F2 作用 下静止在竖直墙面上，如图所示，下列说法正确的是( D ) A．a、b 一定都受四个力的作用 B．a、b 所受摩擦力的方向都是竖直向上 C．F2 一定小于 F1 D．F1、F2 大小可能相等 解析：对 a 受力分析如图 1：除摩擦力外的三个力不可能平衡，故一定有摩擦力，摩擦力方向竖直向上， 故 a 受四个力；除摩擦力外对 b 受力分析如图 2：除摩擦力外，N、F2、 mg 三力有可能平衡，沿竖直方向 和水平方向分解 F2，设 F2 与竖直方向夹角为α则有：F2cos α＝mg，F2sin α＝N，解得 F2＝mgcos α；(1) 若 F2＝mgcos α没有摩擦力，此时 b 受 3 个力；(2)若 F2>mgcos α，摩擦力向下，b 受四个力；(3)若 F2