- 161.86 KB
- 2021-05-24 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
第06讲 共点力的合成与分解
【教学目标】
1.会用平行四边形定则、三角形法则进行力的合成与分解.
2.会用正交分解法进行力的合成与分解.
【教学过程】
★重难点一、力的合成问题★
一、 力的合成问题
1.共点力合成的常用方法
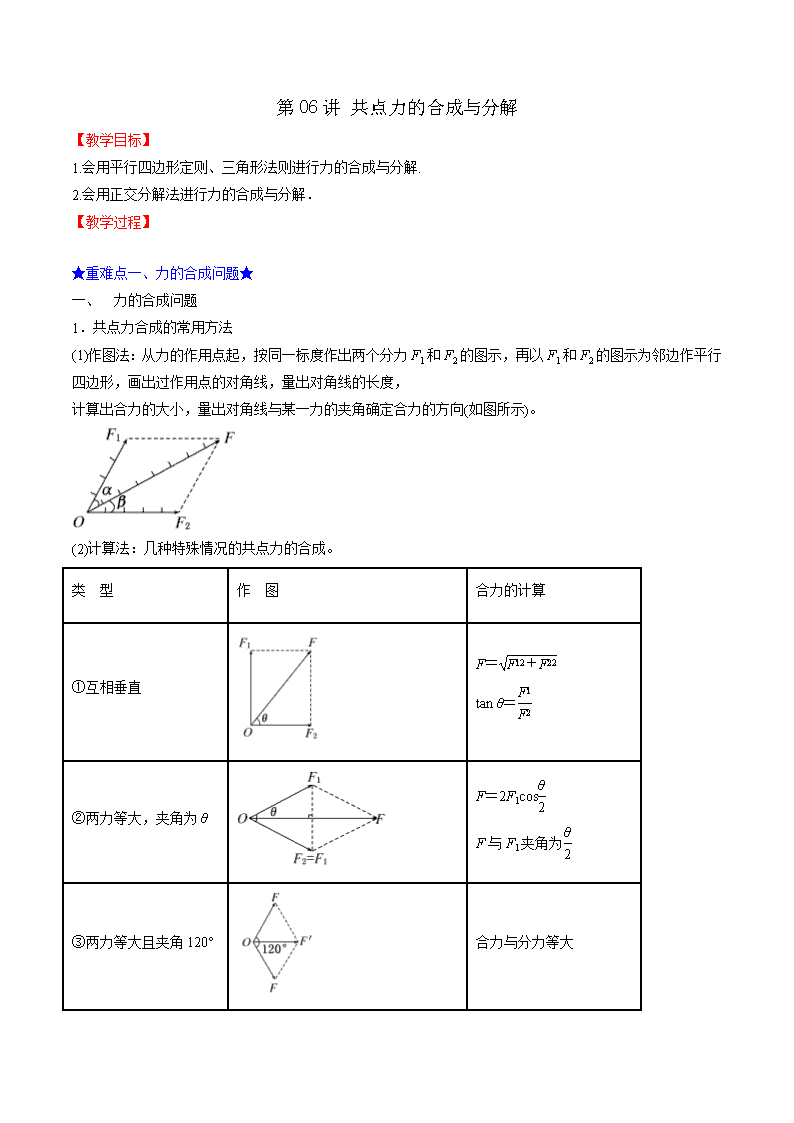
(1)作图法:从力的作用点起,按同一标度作出两个分力F1和F2的图示,再以F1和F2的图示为邻边作平行四边形,画出过作用点的对角线,量出对角线的长度,
计算出合力的大小,量出对角线与某一力的夹角确定合力的方向(如图所示)。
(2)计算法:几种特殊情况的共点力的合成。
类 型
作 图
合力的计算
①互相垂直
F=
tan θ=
②两力等大,夹角为θ
F=2F1cos
F与F1夹角为
③两力等大且夹角120°
合力与分力等大
2.合力的大小范围
(1)两个共点力的合成
|F1-F2|≤F合≤F1+F2
即两个力大小不变时,其合力随夹角的增大而减小,当两力反向时,合力最小,为|F1-F2|,当两力同向时,合力最大,为F1+F2。
(2)三个共点力的合成
①三个力共线且同向时,其合力最大,为F1+F2+F3。
②任取两个力,求出其合力的范围,如果第三个力在这个范围之内,则三个力的合力最小值为零;如果第三个力不在这个范围内,则合力最小值等于最大的力减去另外两个力。
【典型例题】(多选)两个互成角度(不为零或180°)共点力F1、F2的大小均为10N,则它们的合力:()
A. 一定大于10N B. 可能等于1N
C. 方向不可能与F1相同 D. 方向不可能同时与F1、F2的方向垂直
【答案】BCD
★重难点二、力的分解问题★
一、 力的分解的两种方法
1.按作用效果分解力的一般思路
2.正交分解法
(1)定义:将已知力按互相垂直的两个方向进行分解的方法。
(2)建立坐标轴的原则:一般选共点力的作用点为原点,在静力学中,以少分解力和容易分解力为原则(即尽量多的力在坐标轴上);在动力学中,习惯以加速度方向和垂直加速度方向为坐标轴建立坐标系。
(3)方法:物体受到多个力作用F1、F2、F3…求合力F时,可把各力沿相互垂直的x轴、y轴分解。
x轴上的合力:
Fx=Fx1+Fx2+Fx3+…
y轴上的合力:
Fy=Fy1+Fy2+Fy3+…
合力大小:
合力方向:与x轴夹角设为θ,则tanθ=。
【特别提醒】
(1)在实际问题中进行力的分解时,有实际意义的分解方法是按力的实际效果进行分解。
(2)力的正交分解是在物体受三个或三个以上的共点力作用下求合力的一种方法,分解的目的是为了更方便地求合力,将矢量运算转化为代数运算。
(3)应用正交分解法解题时,建立坐标系的原则。合力方向在一个坐标轴上,另一个坐标轴的方向合力为零。
【典型例题】如图所示,墙上有两个钉子a和b,它们的连线与水平方向的夹角为45°,两者的高度差为l。一条不可伸长的轻质细绳一端固定于a点,另一端跨过光滑钉子b悬挂一质量为m1的重物。在绳上距a端的c点有一固定绳圈。若绳圈上悬挂质量为m2的钩码,平衡后绳的ac段正好水平,则重物和钩码的质量比为
A. B.2 C. D.
【审题指导】
①重新平衡后的物理情境如何?
②钩码的拉力分别在什么方向产生了作用效果?能否按力的作用效果方向分解?
③c点共受到几个力的作用?能否用正交分解法求解?
【答案】 C
【解析】 解法一 力的效果分解法
钧码的拉力F等于钩码重力m2g,将F沿ac和bc方向分解,两个分力分别为Fa、Fb,如图甲所示,其中Fb=m1g,由几何关系可得cos θ==,又由几何关系得cos θ=,联立解得=。
解法二 正交分解法
绳圈受到Fa、Fb、F三个力作用,如图乙所示,将Fb沿水平方向和竖直方向正交分解,由竖直方向受力平衡得m1gcos θ=m2g;由几何关系得cos θ=,联立解得=。
★重难点三、绳上的“死结”和“活结”模型★
绳上的“死结”和“活结”模型
1.“死结”模型的4个特点
(1)“死结”可理解为把绳子分成两段;
(2)“死结”是不可以沿绳子移动的结;
(3)“死结”两侧的绳因结住而变成了两根独立的绳;
(4)“死结”分开的两段绳子上的弹力不一定相等。
2.“活结”模型的4个特点
(1)“活结”可理解为把绳子分成两段;
(2)“活结”是可以沿绳子移动的结点;
(3)“活结”一般是由绳跨过滑轮或者绳上挂一光滑挂钩而形成的。绳子虽然因“活结”而弯曲,但实际上是同一根绳;
(4)“活结”分开的两段绳子上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的平分线。
【特别提醒】
(1)“死结”模型中的杆与墙的连结一般为链铰,因而杆上的力沿杆、绳上的力沿绳。
(2)“活结”模型中的杆一般固定住,故杆对滑轮的力不一定沿杆,与绳对滑轮的力平衡。
【典型例题】如图甲所示,轻绳AD跨过固定的水平横梁BC右端的定滑轮挂住一个质量为M1的物体,∠ACB=30°;图乙中轻杆HG一端用铰链固定在竖直墙上,另一端G通过细绳FG拉住,EG与水平方向也成30°,轻杆的G点用细绳GF拉住一个质量为M2的物体,求:
(1)轻绳AC段的张力FAC与细绳EG的张力FEG大小之比;
(2)轻杆BC对C端的支持力;
(3)轻杆HG对G端的支持力。
【审题指导】
抓关键点:
甲:固定杆连“活结”。
乙:铰链杆连“活结”。
找突破口:
甲中杆对滑轮的合力与两绳的合力平衡,乙中杆上的力沿杆。
【答案】 (1) (2)M1g 方向和水平方向成30°指向右上方 (3)M2g 方向水平向右
【解析】 题图甲和乙中的两个物体M1、M2都处于平衡状态,根据平衡的条件,首先判断与物体相连的细绳,其拉力大小等于物体的重力;分别取C点和G点为研究对象,进行受力分析如图甲和乙所示,根据平衡规律可求解。
(1)图甲中轻绳AD跨过定滑轮拉住质量为M1的物体,物体处于平衡状态,轻绳AC段的拉力FAC=FCD=M1g
图乙中由于FEGsin 30°=M2g,得FEG=2M2g。
所以=。
(2)图甲中,三个力之间的夹角都为120°,根据平衡规律有NC=FAC=M1g,方向和水平方向成30°,指向右上方。
(3)图乙中,根据平衡方程有FEGsin 30°=M2g,FEGcos 30°=NG,所以NG=M2gcot 30°=M2g,方向水平向右。