【物理】2019届一轮复习人教版 力与直线运动 学案 15页

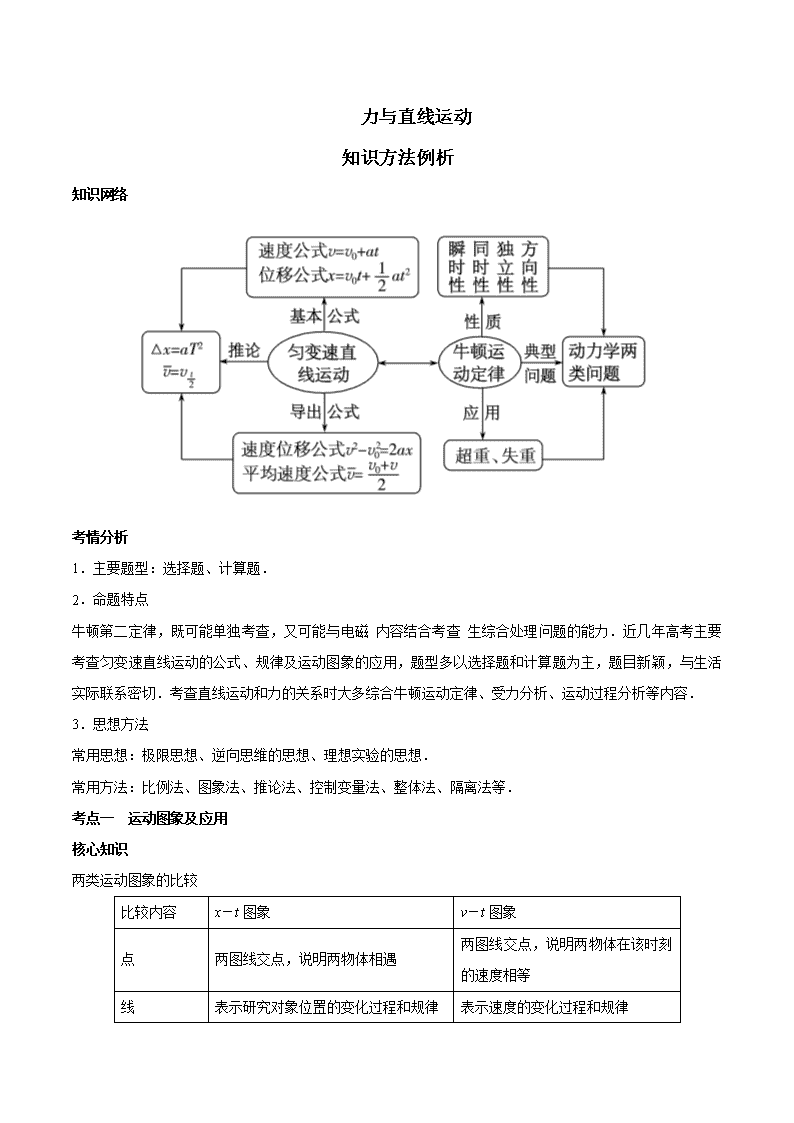
‎ 力与直线运动 知识方法例析 知识网络 考情分析 ‎1．主要题型：选择题、计算题．‎ ‎2．命题特点 牛顿第二定律，既可能单独考查，又可能与电磁 内容结合考查 生综合处理问题的能力．近几年高考主要考查匀变速直线运动的公式、规律及运动图象的应用，题型多以选择题和计算题为主，题目新颖，与生活实际联系密切．考查直线运动和力的关系时大多综合牛顿运动定律、受力分析、运动过程分析等内容．‎ ‎3．思想方法 常用思想：极限思想、逆向思维的思想、理想实验的思想．‎ 常用方法：比例法、图象法、推论法、控制变量法、整体法、隔离法等．‎ 考点一　运动图象及应用 核心知识 两类运动图象的比较 比较内容 x－t图象 v－t图象 点 两图线交点，说明两物体相遇 两图线交点，说明两物体在该时刻的速度相等 线 表示研究对象位置的变化过程和规律 表示速度的变化过程和规律 斜率 大小 表示物体速度的大小 表示物体加速度的大小 正负 表示物体速度的方向 表示加速度的方向 截距 纵轴截距表示t＝0时刻的初始位移，横轴截距表示位移为零的时刻 纵轴截距表示t＝0时刻的初速度，横轴截距表示速度为零的时刻 面积 ‎—‎ 数值上表示某段时间内的位移 描述运动 直线运动 直线运动 图象意义 位置随时间变化并非实际运动轨迹 速度随时间变化并非实际运动轨迹 规律方法 图象问题要四看一注意 ‎(1)看坐标轴：看清坐标轴所表示的物理量，明确因变量(纵轴表示的量)与自变量 (横轴表示的量)之间的制约关系．‎ ‎(2)看图象：识别两个相关量的变化趋势，从而分析具体的物理过程．‎ ‎(3)看纵坐标、“斜率”和“面积”；v－t图象中根据坐标值、“斜率”和“面积”可分析速度、加速度和位移的大小、方向特点．x－t图象中根据坐标值、“斜率”可分析位移、速度的大小、方向特点．‎ ‎(4)看交点：明确图线与图线的交点、图线与坐标轴的交点的物理意义．‎ ‎(5)一注意：利用v－t图象分析两个物体的运动时，要注意两个物体的出发点，即注意它们是从同一位置出发，还是从不同位置出发．若从不同位置出发，要注意出发时两者的距离．‎ 典例分析 ‎【例1】　(2017年江西宜春三中高三期中)甲、乙两质点同时沿同一直线运动，速度随时间变化的v－t图象如图所示，关于两质点的运动情况，下列说法正确的是(　　)‎ A．在t＝0时，甲、乙的运动方向相同 B．在0－t0内，乙的加速度先增大后减小 C．在0－2t0内，乙的平均速度等于甲的平均速度 D．若甲、乙从同一位置出发，则t0时刻相距最远 ‎【分析】　v－t 图象中，速度的正负表示物体的运动方向．倾斜的直线表示匀变速直线运动，斜率表示加速度，图象与坐标轴围成的面积表示位移．在时间轴上方的位移为正，在时间轴下方位移为负，通过分析两个物体的运动情况进行判断．‎ ‎【答案】　D 速度，两者间距减小，所以t0时刻相距最远，故D正确．‎ ‎【例2】　(2017年河北唐山开滦二中高三期中)甲、乙两质点沿同一方向做直线运动，某时刻经过同一地点．若以该时刻作为计时起点，得到两质点的x－t图象如图所示，图象中的OC与AB平行，CB与OA平行．则下列说法中正确的是(　　)‎ A．t1－t2时间内甲和乙的距离越来越远 B．0－t2时间内甲的速度和乙的速度始终不相等 C．0－t3时间内甲和乙的位移相等 D．0－t3时间内甲的平均速度大于乙的平均速度 ‎【答案】　C ‎【解析】　图象的纵坐标表示物体所在的位置；由题图可知t1到t2时刻甲、乙的距离始终不变，故A错误；图象的斜率表示物体的速度，由题图可知，t1－t2时间内甲的速度和乙的速度相等，故B错误；根据位移等于x的变化量，由题图可知，0－t3时间内甲和乙的位移相等，故C正确；0－t3时间内，甲和乙的位移相等，所用时间相等，则二者平均速度相等，故D错误． 4 ‎ ‎【例3】　(多选)一质点在力的作用下沿x轴正方向做直线运动，通过坐标原点时开始计时，其－t图象如图所示，则(　　)‎ A．质点做匀速直线运动，速度为0.5 m/s B．质点做匀变速直线运动，加速度大小为1 m/s2‎ C．质点在1 s末速度为0.5 m/s D．质点2 s末回到出发点 ‎【答案】　BD 发点，故D正确．‎ 规律总结 解图象类问题的关键,将图象与物理过程对应起来，通过图象的坐标轴、关键点、斜率、截距、面积等信息，对运动过程进行分析，从而解决问题.‎ 考点二　匀变速直线运动规律的应用 核心知识 规律方法 ‎1．求解匀变速直线运动问题的一般思路 →→→→→ ‎2．匀变速直线运动常用的五种解题方法 ‎3．处理刹车类问题的思路 ‎ 先判断刹车时间，再进行分析计算．‎ 典例分析 ‎【例1】　(多选)在足够长的光滑斜面上，有一物体以10 m/s的初速度沿斜面向上运动，物体的加速度始终为5 m/s2，方向沿斜面向下，当物体的位移大小为7.5 m时，下列说法正确的是(　　)‎ A．物体运动时间可能为1 s B．物体运动时间可能为3 s C．物体运动时间可能为(2＋)s D．此时的速度大小一定为5 m/s ‎【答案】　ABC ‎【解析】　(1)物体在出发点上方时，由x＝v0t＋at2得：7.5＝10t＋×(－5)t2，解得t＝1 s或t＝3 s，由v＝v0＋at得，v＝5 m/s或－5 m/s.‎ ‎(2)物体在出发点下方时，由x＝v0t＋at2得：－7.5＝10t＋×(－5)t2，解得t＝(2＋)s或t＝(2－)s(舍去)，由v＝v0＋at得：v＝－5m/s.故A、B、C正确，D错误．‎ ‎【例2】　(2017年河北石家庄模拟)t＝0时刻，物体由静止开始做匀加速直线运动，已知2 s末的速度大小为8 m/s，则(　　)‎ A．物体的加速度大小为8 m/s2‎ B．物体在2 s内的平均速度大小为8 m/s C．物体在第2 s内的位移大小为8 m D．物体在2 s内的位移大小为8 m ‎【答案】　D ‎【例3】　如图所示，倾角为30°的足够长光滑斜面下端与另一足够长光滑水平面相接，连接处用一光滑小圆弧过渡，斜面上距水平面高度分别为h1＝5 m和h2＝0.2 m的两点上，各静置一小球A和B.某时刻由静止开始释放A球，经过一段时间t后，再由静止开始释放B球．g取10 m/s2.‎ ‎ (1)为了保证A、B两球不会在斜面上相碰，t最长不能超过多少？‎ ‎(2)若A球从斜面上h1高度处自由下滑的同时，B球受到恒定外力作用从斜面底端C点以加速度a由静止开始向右运动，则a最大为多大时，A球能追上B球？‎ ‎【答案】（1）1.6s（2）2.5m/s2‎ 解得t1＝2 s，t2＝0.4 s 为了保证A、B两球不会在斜面上相碰，t最长不能超过 t＝t1－t2＝1.6 s ‎(2)设A球在水平面上再经t0追上B球，‎ 则a(t1＋t0)2＝(gsin30°)t1t0‎ A球要追上B球，上述方程必须有解，‎ 即(2a－10)2－4a2≥0，解得a≤2.5 m/s2. 3 ‎ 规律总结 ‎1.求解匀变速直线运动问题时的方法技巧,在涉及匀变速直线运动题目中，如果出现相等时间关系，则要优先使用中间时刻速度及相邻相等时间T内位移差公式xn－xm＝(n－m)aT2，如果题中给出初(或末)速度为0，则优先用初速度为0的匀变速直线运动的“比例公式”.‎ ‎2.求解追及相遇问题 考点三　牛顿定律的应用 核心知识 ‎1．牛顿第二定律的表达式 F合＝ma.‎ ‎2．牛顿第二定律的“四性”‎ ‎(1)矢量性：公式F＝ma是矢量式，a与F方向相同．‎ ‎(2)瞬时性：力与加速度同时产生，同时变化，同时消失．‎ ‎(3)同体性：F＝ma中，F、m、a对应同一物体．‎ ‎(4)独立性：分力产生的加速度相互独立，与其他加速度无关．‎ 规律方法 ‎1．牛顿第二定律解题时明确整体法与隔离法的选择 ‎(1)整体法：‎ ‎①优点：研究对象减少，忽略物体之间的相互作用力，方程数减少，求解简捷．‎ ‎②条件：连接体中各物体具有共同的加速度．‎ ‎(2)隔离法：‎ ‎①优点：易看清各个物体具体的受力情况．‎ ‎②条件：当系统内各物体的加速度不同时，一般采用隔离法；求连接体内各物体间的相互作用力时必须用隔离法．‎ ‎2．两类模型 ‎(1)刚性绳(或接触面)——不发生明显形变就能产生弹力的物体，剪断(或脱离)后，其弹力立即消失，不需要形变恢复时间．‎ ‎(2)弹簧(或橡皮绳)——两端同时连接(或附着)有物体的弹簧(或橡皮绳)，特点是形变量大，其形变恢复需要较长时间，在瞬时性问题中，其弹力的大小往往可以看成保持不变．‎ 典例分析 ‎【例1】　(2017年江西九江一中高三月考)如图所示，A、B、C三球的质量均为m，轻质弹簧一端固定在斜面顶端、另一端与A球相连，A、B间固定一个轻杆，B、C由一轻质细线连接．倾角为θ的光滑斜面固定在地面上，弹簧、轻杆与细线均平行于斜面，初始时系统处于静止状态，细线被烧断的瞬间，下列说法正确的是(　　)‎ A．B球的受力情况未变，加速度为零 B．A、B两个小球的加速度均沿斜面向上，大小均为gsinθ C．A、B之间杆的拉力大小为mgsinθ D．C球的加速度沿斜面向下，大小为gsinθ ‎【分析】　细线断前三者保持平衡状态，列平衡方程可求得弹簧及绳的弹力，断后A、B作为整体会向上运动，C向下运动，分别以A、B组成的系统、B、C为研究对象，由牛顿第二定律分析答题．‎ ‎【答案】　BCD 方向沿斜面向下，故D正确．‎ ‎【例2】　(2017年东北三省三校第一次联考)如图所示，位于竖直平面内的固定光滑圆环轨道与水平面相切于M点，与竖直墙相切于A点．竖直墙上另一点B与M的连线和水平面的夹角为60°，C 是圆环轨道的圆心．已知在同一时刻a、b两球分别由A、B两点从静止开始沿光滑倾斜直轨道AM、BM运动到M点；c球由C点自由下落到M点．则(　　)‎ A．a球最先到达M点 B．b球最先到达M点 C．c球最先到达M点 D．b球和c球都可能最先到达M点 ‎【答案】　C 上所述可得tb>ta>tc.‎ ‎【例3】　如图甲所示，为一倾角θ＝37°的足够长斜面，将一质量为m＝1 g的物体无初速度在斜面上释放，同时施加一沿斜面向上的拉力，拉力随时间变化的关系图象如图2－3－4乙所示，物体与斜面间的动摩擦因数μ＝0.25，取g＝10 m/s2，sin37°＝0.6，cos37°＝0.8，求：‎ ‎ (1)2 s末物体的速度；‎ ‎(2)前16 s内物体发生的位移．‎ ‎【答案】（1）5 m/s，方向沿斜面向下（2）30 m ‎【解析】　(1)由分析可知物体在前2 s内沿斜面向下做初速度为零的匀加速直线运动，由牛顿第二定律可得mgsinθ－F1－μmgcosθ＝ma1，v1＝a1t1，‎ 代入数据可得a1＝2.5 m/s2，方向沿斜面向下 v1＝5 m/s，方向沿斜面向下 ‎(2)物体在前2 s内发生的位移为x1，则x1＝a1t＝5 m，方向沿斜面向下，当拉力为F2＝4.5 N时，由牛顿第二定律可得 F2＋μmgcosθ－mgsinθ＝ma2‎ 代入数据可得a2＝0.5 m/s2，方向沿斜面向上 物体经过t2时间速度减为0，则v1＝a2t2，得t2＝10 s t2时间内发生的位移为x2，则x2＝a2t＝25 m，方向沿斜面向下 由于mgsinθ－μmgcosθv时，可能一直减速，也可能先减速再匀速 ‎(2)v0v，返回时速度为v；当v0a0则发生相对滑动．‎ ‎②若a≤a0则能相对静止．‎ 考点五　滑块、滑板模型 核心知识 ‎1．模型构建 上、下叠放两个物体，并且两物体在拉力和摩擦力的相互作用下发生相对滑动．‎ ‎2．模型条件 上、下叠放的两个物体分别在各自所受力的作用下完成各自的运动，且两者之间还有相对运动．‎ ‎3．模型特点 ‎(1)该模型存在判断是否存在速度相等的“临界点”，来判定临界速度之后两者的运动形式．‎ ‎(2)两种位移关系，滑块由滑板的一端运动到另一端的过程中，若滑块和滑板同向运动，位移之差等于板长；反向运动时，位移之和等于板长．‎ 规律方法 滑块、滑板类模型的解题方法 典例分析 ‎【例】　如图所示，可看成质点的小物块放在长木板正中间，已知长木板质量M＝4 g，长度L＝2 m，小物块质量m＝1 g，长木板置于光滑水平地面上，两物体皆静止．现在用一大小为F的水平恒力作用于小物块上，发现只有当F超过2.5 N时，才能让两物体间产生相对滑动，设两物体间的最大静摩擦力大小等于滑动摩擦力大小，重力加速度g＝10 m/s2，试求：‎ ‎ (1)小物块和长木板间的动摩擦因数； ‎ ‎(2)若一开始力F就作用在长木板上，且F＝12 N，则小物块经过多长时间从长木板上掉下？‎ ‎【答案】（1）0.2（2）2s ‎【解析】　(1)设两物体间的最大静摩擦力为Ff，当F＝2.5 N作用于小物块时，对整体由牛顿第二定律有 F＝(M＋m)a①‎ 对长木板由牛顿第二定律有Ff＝Ma②‎ 由①②可得Ff＝2 N 小物块竖直方向上受力平衡，所受支持力FN＝mg，摩擦力Ff＝μmg得μ＝0.2 ‎ 由匀变速直线运动规律，两物体在t时间内的位移分别为 s1＝a1t2‎ s2＝a2t2‎ 小物块刚滑下长木板时，有s1－s2＝L 解得t＝2 s。 · 1 ‎