高中物理磁场经典计算题训练--人教版 20页

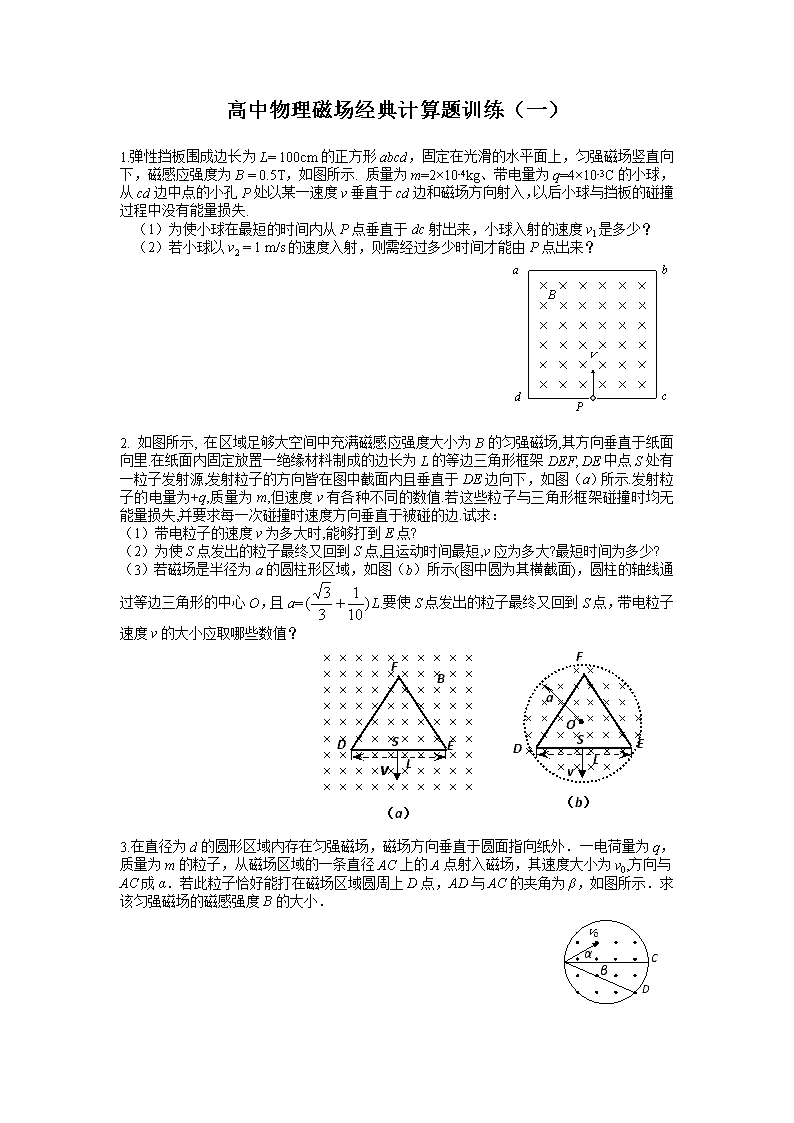
高中物理磁场经典计算题训练（一） 1.弹性挡板围成边长为 L= 100cm的正方形 abcd，固定在光滑的水平面上，匀强磁场竖直向 下，磁感应强度为 B = 0.5T，如图所示. 质量为 m=2×10-4kg、带电量为 q=4×10-3C的小球， 从 cd边中点的小孔 P处以某一速度 v垂直于 cd边和磁场方向射入，以后小球与挡板的碰撞 过程中没有能量损失. （1）为使小球在最短的时间内从 P点垂直于 dc射出来，小球入射的速度 v1是多少？ （2）若小球以 v2 = 1 m/s的速度入射，则需经过多少时间才能由 P点出来？ 2. 如图所示, 在区域足够大空间中充满磁感应强度大小为 B的匀强磁场,其方向垂直于纸面 向里.在纸面内固定放置一绝缘材料制成的边长为 L的等边三角形框架 DEF, DE中点 S处有 一粒子发射源,发射粒子的方向皆在图中截面内且垂直于 DE边向下，如图（a）所示.发射粒 子的电量为+q,质量为 m,但速度 v有各种不同的数值.若这些粒子与三角形框架碰撞时均无能 量损失,并要求每一次碰撞时速度方向垂直于被碰的边.试求： （1）带电粒子的速度 v为多大时,能够打到 E点? （2）为使 S点发出的粒子最终又回到 S点,且运动时间最短,v应为多大?最短时间为多少? （3）若磁场是半径为 a的圆柱形区域，如图（b）所示(图中圆为其横截面)，圆柱的轴线通 过等边三角形的中心 O，且 a= ) 10 1 3 3(  L.要使 S点发出的粒子最终又回到 S点，带电粒子 速度 v的大小应取哪些数值？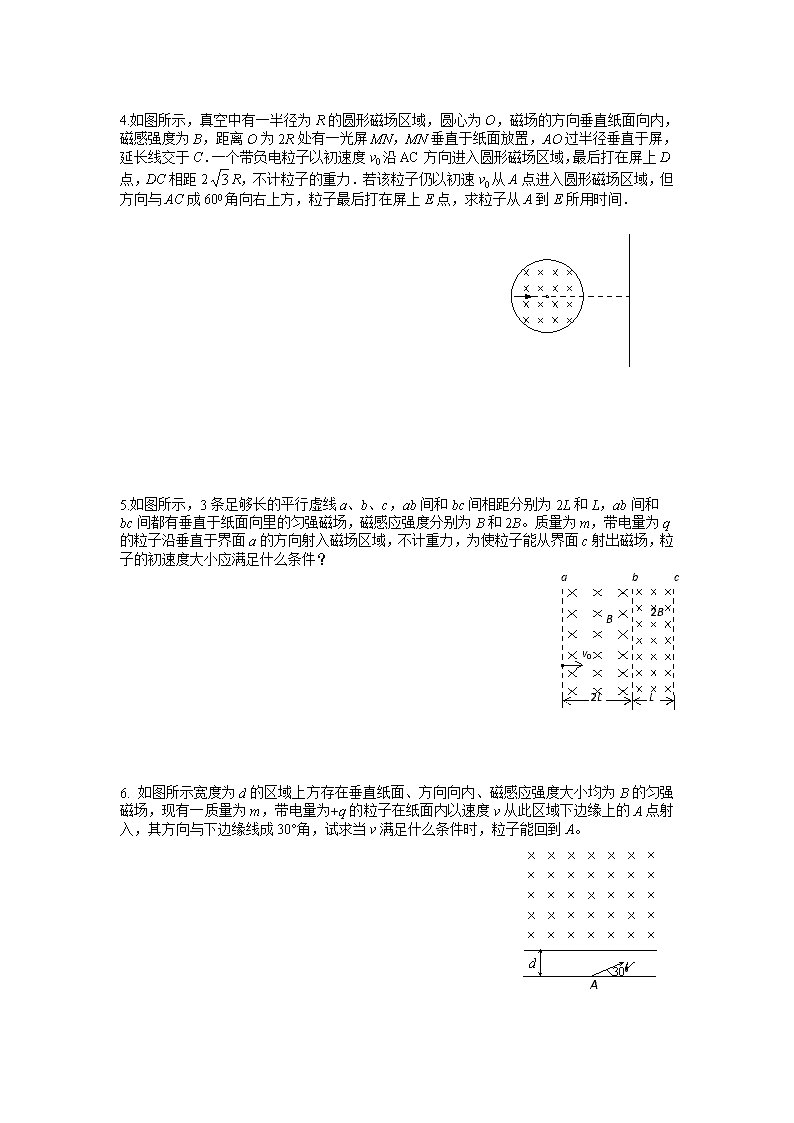 3.在直径为 d的圆形区域内存在匀强磁场，磁场方向垂直于圆面指向纸外．一电荷量为 q， 质量为 m的粒子，从磁场区域的一条直径 AC上的 A点射入磁场，其速度大小为 v0,方向与 AC成α．若此粒子恰好能打在磁场区域圆周上 D点，AD与 AC的夹角为β，如图所示．求 该匀强磁场的磁感强度 B的大小． a b cd B P v A C D α β v0 L B v ES F D （a） a O ES F D L v （b） 4.如图所示，真空中有一半径为 R的圆形磁场区域，圆心为 O，磁场的方向垂直纸面向内， 磁感强度为 B，距离 O为 2R处有一光屏 MN，MN垂直于纸面放置，AO过半径垂直于屏， 延长线交于 C．一个带负电粒子以初速度 v0沿 AC方向进入圆形磁场区域，最后打在屏上 D 点，DC相距 2 3 R，不计粒子的重力．若该粒子仍以初速 v0从 A点进入圆形磁场区域，但 方向与 AC成 600角向右上方，粒子最后打在屏上 E点，求粒子从 A到 E所用时间． 5.如图所示，3条足够长的平行虚线 a、b、c，ab间和 bc间相距分别为 2L和 L，ab间和 bc间都有垂直于纸面向里的匀强磁场，磁感应强度分别为 B和 2B。质量为 m，带电量为 q 的粒子沿垂直于界面 a的方向射入磁场区域，不计重力，为使粒子能从界面 c射出磁场，粒 子的初速度大小应满足什么条件？ 6. 如图所示宽度为 d的区域上方存在垂直纸面、方向向内、磁感应强度大小均为 B的匀强 磁场，现有一质量为 m，带电量为+q的粒子在纸面内以速度 v从此区域下边缘上的 A点射 入，其方向与下边缘线成 30°角，试求当 v满足什么条件时，粒子能回到 A。 2L L v0 B 2B a b c A O C M N d 300 v A 7.在受控热核聚变反应的装置中温度极高，因而带电粒子没有通常意义上的容器可装，而 是由磁场将带电粒子的运动束缚在某个区域内。现有一个环形区域，其截面内圆半径 R1= 3 3 m，外圆半径 R2=1.0m，区域内有垂直纸面向外的匀强磁场（如图所示）。已知磁感 应强度 B＝1.0T，被束缚带正电粒子的荷质比为 m q ＝4.0×107C/kg，不计带电粒子的重力和 它们之间的相互作用． ⑴若中空区域中的带电粒子由 O点沿环的半径方向射入磁场，求带电粒子不能穿越 磁场外边界的最大速度 v0。 ⑵若中空区域中的带电粒子以⑴中的最大速度 v0沿圆环半径方向射入磁场，求带电 粒子从刚进入磁场某点开始到第一次回到该点所需要的时间。 8.空间中存在方向垂直于纸面向里的匀强磁场，磁感应强度为 B，一带电量为+q、质量为 m 的粒子，在 P点以某一初速开始运动，初速方向在图中纸面内如图中 P点箭头所示。该粒 子运动到图中 Q点时速度方向与 P点时速度方向垂直。如图中 Q点箭头所示。已知 P、Q 间的距离为 l。若保持粒子在 P点时的速度不变，而将匀强磁场换成匀强电场，电场方向与 纸面平行且与粒子在 P点时的速度方向垂直，在此电场作用下粒子也由 P点运动到 Q点。 不计重力。求：⑴电场强度的大小。⑵两种情况中粒子由 P运动到 Q点所经历的时间之差。 P Q 参考答案 1、（1）根据题意，小球经 bc、ab、ad的中点垂直反弹后能以最短的时间射出框架，如甲图 所示. 即小球的运动半径是 R = L 2 = 0.5 m ① 由牛顿运动定律 qv1B = m v12 R ② 得 v1 = qBR m ③ 代入数据得 v1 = 5 m/s ④ （2）由牛顿运动定律 qv2B = m v22 R2 ⑤ 得 R2 = mv2 qB = 0.1 m ⑥ 由题给边长知 L = 10R2 ⑦ 其轨迹如图乙所示.由图知小球在磁场中运动的周期数 n = 9 ⑧ 根据公式 T = 2m qB = 0.628 s ⑨ 小球从 P点出来的时间为 t = nT = 5.552 s ⑩ 甲 乙 2. (1)从 S点发射的粒子将在洛仑兹力作用下做圆周运动, 即 R mvqvB 2  ① -------------------（2分） 因粒子圆周运动的圆心在 DE 上,每经过半个园周打到 DE 上一次，所以粒子要打到 E 点应满足：  3,2,1,2 2 1  nRnL ② -------------------（2分） 由①②得打到 E点的速度为 nm qBLv 4  ，  3,2,1n ------------（2分） 说明：只考虑 n=1的情况，结论正确的给 4分。 (2) 由题意知, S点发射的粒子最终又回到 S点的条件是 )3,2,1(, 12 1 212      n n L n ESR 在磁场中粒子做圆周运动的周期 qB m v RT  22  ,与粒子速度无关,所以, 粒子圆周运 动的次数最少,即 n=1时运动的时间最短, 即当： 2 L qB mvR  时时间最短 ---------------（2分） 粒子以三角形的三个顶点为圆心运动,每次碰撞所需时间: Tt 6 5 1  ------（2分） 经过三次碰撞回到 S点,粒子运动的最短时间 qB mTtt 5 2 53 1  -------（2分） (3)设 E点到磁场区域边界的距离为 L ,由题设条件知 1030cos 1 2 0 LLaL  -------------------（1分） S点发射的粒子要回到 S点就必须在磁场区域内运动,即满足条件: a b cd P v a b cd P v LR  ,即 10 LR  又知 )3,2,1(, 12 1 212      n n L n ESR , -------------------（1分） 当 1n 时, 2 LR  当 2n 时, 6 LR  当 3n 时, 10 LR  当 4n 时, 14 LR  所以,当 5,4,3n 时,满足题意. 3. 设粒子在磁场中做圆周运动的半径为 R，则有 qv0B=m R 2 0v ①圆心在过 A与 v0方向垂 直的直线上，它到 A 点距离为 R，如图所示，图中直线 AD 是圆轨道的弦，故有 ∠OAD=∠ODA，用γ表示此角度，由几何关系知 2Rcosγ=AD ② dcosβ=AD ③ α+β+γ=π/2 ④ 解②③④得 R= )sin(2 cos    d ⑤ 代入①得 B=   cos )sin(2 0 qd m v ⑥ 4. 00 2 3 3 3 vv RR   5. m BqL4 0 v （提示：做图如右，设刚好从 c射出 磁场，则α+β=90°，而 BqB mvR 1  ，有 R1=2R2， 设 R2=R，而 2L=2Rsinα，L=R(1-cosβ)，得α=30°， R1=4L。） 6. 粒子运动如图所示，由图示的几何关系可知 d3230tan/d2r  （1） 粒子在磁场中的轨道半径为 r，则有 r mvBqv 2  （2） 联立①②两式，得 m dBq32v  ，此时粒子可按图中轨道返到 A点。 7.（1）如图所示，当粒子以最大速度在磁场中运动时，设运动半径为 r，则： 2 2 22 1 )( rRrR  2L L v0 B 2B a b c R1 R2 α β 解得： 3 1 r m 又由牛顿第二定律得： r mBq 2 0 0 vv  解得： sm /1033.1 7 0 v （2）如图 3 ,31   r Rtg ，带电粒子必须三次经过磁场，才会回到该点 在磁场中的圆心角为  3 4 ，则在磁场中运动的时间为 s Bq mTTt 7 1 1014.342 3 23   在磁场外运动的时间为 s v Rt 7 0 1 2 10 2 3323  故所需的总时间为： sttt 7 21 1074.5  8.⑴ m qlBE 22  ⑵   qB mtt 2 2 21    高中物理磁场经典计算题训练（二） 1.如图所示，一个质量为 m，带电量为+q的粒子以速度 v0从 O点沿 y 轴正方向射入磁感应 强度为 B的圆形匀强磁场区域，磁场方向垂直纸面向外，粒子飞出磁场区域后，从点 b处 穿过 x轴，速度方向与 x轴正方向的夹角为 300.粒子的重力不计，试求: (1)圆形匀强磁场区域的最小面积. (2)粒子在磁场中运动的时间. (3)b到 O的距离. 2．纸平面内一带电粒子以某一速度做直线运动，一段时间后进入一垂直于纸面向里的圆形 匀强磁场区域（图中未画出磁场区域），粒子飞出磁场后从上板边缘平行于板面进入两面平 行的金属板间，两金属板带等量异种电荷，粒子在两板间经偏转后恰从下板右边缘飞出。已 知带电粒子的质量为 m，电量为 q，重力不计。粒子进入磁场前的速度方向与带电板成θ= 60°角，匀强磁场的磁感应强度为 B，带电板板长为 l，板距为 d，板间电压为 U，试解答： ⑴上金属板带什么电？⑵粒子刚进入金属板时速度为多大？⑶圆形磁场区域的最小面积为 多大？ 3.如图所示，在 y>0的区域内有沿 y轴正方向的匀强电场，在 y<0的区域内有垂直坐标平面 向里的匀强磁场。一电子（质量为 m、电量为 e）从 y轴上 A点以沿 x轴正方向的初速度 v0 开始运动。当电子第一次穿越 x轴时，恰好到达 C点；当电子第二次穿越 x轴时，恰好到达 坐标原点；当电子第三次穿越 x轴时，恰好到达 D点。C、D两点均未在图中标出。已知 A、 C点到坐标原点的距离分别为 d、2d。不计电子的重力。求 （1）电场强度 E的大小； （2）磁感应强度 B的大小； （3）电子从 A运动到 D经历的时间 t． E y x v0 O× × × × × × × × × × × × × × × × × × × × × A B θ b x y O m,qv0 30° 4.如图所示，在半径为 R的绝缘圆筒内有匀强磁场，方向垂直纸面向里，圆筒正下方有小孔 C与平行金属板 M、N相通。两板间距离为 d，两板与电动势为 E的电源连接，一带电量为 －q、质量为 m的带电粒子（重力忽略不计），开始时静止于 C点正下方紧靠 N板的 A点， 经电场加速后从 C点进入磁场，并以最短的时间从 C点射出。已知带电粒子与筒壁的 碰撞无电荷量的损失，且碰撞后以原速率返回。求： ⑴筒内磁场的磁感应强度大小； ⑵带电粒子从 A点出发至重新回到 A点射出所经 历的时间。 5.如图所示，空间分布着有理想边界的匀强电场和 匀强磁场。左侧匀强电场的场强大小为 E、方向水平向右，电场宽度为 L；中间区域和右侧 匀强磁场的磁感应强度大小均为 B，方向分别垂直纸面向外和向里。一个质量为 m、电量为 q、不计重力的带正电的粒子从电场的左边缘的 O点由静止开始运动，穿过中间磁场区域进 入右侧磁场区域后，又回到 O点，然后重复上述运动过程。求： （1）中间磁场区域的宽度 d； （2）带电粒子从 O点开始运动到第一次回到 O点所用时间 t。 6.如图所示，粒子源 S可以不断地产生质量为 m、电荷量为+q的粒子(重力不计)．粒子从 O1孔漂进(初速不计)一个水平方向的加速电场，再经小孔 O2进入相互正交的匀强电场和匀 强磁场区域，电场强度大小为 E，磁感应强度大小为 B1，方向如图．虚线 PQ、MN之间存 在着水平向右的匀强磁场，磁感应强度大小为 B2．有一块折成直角的硬质塑料板 abc(不带 电，宽度很窄，厚度不计)放置在 PQ、MN之间(截面图如图)，a、c两点恰在分别位于 PQ、 MN上，ab=bc=L，α= 45°．现使粒子能沿图中虚线 O2O3进入 PQ、MN之间的区域． (1) 求 加速电压 U1． (2) 假设粒子与硬质塑料板相碰后，速度大小不变，方向变化遵守光的反射 定律．粒子在 PQ、MN之间的区域中运动的时间和路程分别是多少？ 7.如图所示，K与虚线 MN之间是加速电场.虚线 MN与 PQ之间是匀强电场，虚线 PQ与荧 A B CM N Ed -q,m R + + + + + + + + S O1 O2 B2 B1 U11 E P Q a b cα － － － － － － － α M N O3 B BE L d O 光屏之间是匀强磁场，且 MN、PQ与荧光屏三者 互相平行.电场和磁场的方向如图所示.图中A点与 O点的连线垂直于荧光屏.一带正电的粒子从 A点 离开加速电场，速度方向垂直于偏转电场方向射 入偏转电场，在离开偏转电场后进入匀强磁场， 最后恰好垂直地打在荧光屏上.已知电场和磁场区 域在竖直方向足够长，加速电场电压与偏转电场 的场强关系为 U= 2 1 Ed，式中的 d是偏转电场的宽 度，磁场的磁感应强度 B与偏转电场的电场强度 E和带电粒子离开加速电场的速度 v0关系 符合表达式 v0= B E ，若题中只有偏转电场的宽度 d为已知量，则： （1）画出带电粒子轨迹示意图； （2）磁场的宽度 L为多少？ （3）带电粒子在电场和磁场中垂直于 v0方向的偏转距离分别是多少？ 8.在如图所示的直角坐标中，x轴的上方有与 x轴正方向成 45°角的匀强电场，场强的大小为 E＝ 2 ×104V/m。x轴的下方有垂直于 xOy面的匀强磁场，磁感应强度的大小为 B＝2× 10－2T。把一个比荷为 q/m=2×108C/㎏的正电荷从坐标为（0，1.0）的 A点处由静止释放。电 荷所受的重力忽略不计，求： ⑴电荷从释放到第一次进入磁场时所用的时间 t； ⑵电荷在磁场中的轨迹半径； ⑶电荷第三次到达 x轴上的位置。 9. 如图所示，与纸面垂直的竖直面 MN 的左侧空间中存在竖直向上场强大小为 E=2.5×102N/C的匀强电场(上、下及左侧无界).一个质量为 m=0.5kg、电量为 q=2.0×10—2C的 可视为质点的带正电小球，在 t=0时刻以大小为 v0的水平初速度向右通过电场中的一点 P， 当 t=t1时刻在电场所在空间中加上一如图所示随时间周期性变化的磁场，使得小球能竖直向 下通过 D点，D为电场中小球初速度方向上的一点，PD间距为 L，D到竖直面 MN的距离 DQ为 L/π.设磁感应强度垂直纸面向里为正.(g=10m/s2) (1)如果磁感应强度 B0为已知量，试推出满足条件时 t1的表达式(用题中所给物理量的符 号表示) (2)若小球能始终在电场所在空间做周期性运动.则当小球运动的周期最大时，求出磁感 应强度 B0及运动的最大周期 T的大小. (3)当小球运动的周期最大时，在图中画出小球运动一个周期的轨迹. x/m y/m O 1 B E －2 21—1 45° AE P E M M QDv0 B0 B t 10.如图所示，MN、PQ是平行金属板，板长为 L，两板间距离为 d，在 PQ板的上方有垂直 纸面向里的匀强磁场。一个电荷量为 q、质量为 m的带负电粒子以速度 v0从 MN板边缘沿 平行于板的方向射入两板间，结果粒子恰好从 PQ板左边缘飞进磁场，然后又恰好从 PQ板 的右边缘飞进电场。不计粒子重力。试求： （1）两金属板间所加电压 U的大小； （2）匀强磁场的磁感应强度 B的大小； （3）在图中画出粒子再次进入电场的运动轨迹，并标 出粒子再次从电场中飞出的位置与速度方向。 11.如图所示，真空中有以 O1为圆心，r为半径的圆形匀强 磁场区域，坐标原点 O为圆形磁 场边界上的一点。磁场的磁感应强度大小为 B，方向垂直于纸面向外。x＝r的虚线右侧足够 大的范围内有方向竖直向下、大小为 E的匀强电场。从 O点在纸面内向各个不同方向发射 速率相同的质子，设质子在磁场中的偏转半径也为 r，已知质子的电荷量为 e，质量为 m。 求： (1) 质子射入磁场时的速度大小； (2) 沿 y轴正方向射入磁场的质子到达 x轴所需的时间； (3) 速度方向与 x轴正方向成 120°角射入磁场的质子到达 x轴时的位置坐标。 12. 如图所示，在坐标系 xOy中，过原点的直线 OC与 x轴正向的夹角＝120，在 OC右侧 有一匀强电场，在第二、三象限内有一匀强磁场，其上边界与电场边界重叠，右边界为 y 轴，左边界为图中平行于 y轴的虚线，磁场的磁感应强度大小为 B，方向垂直于纸面向里。 一带正电荷 q、质量为 m的粒子以某一速度自磁场左边界上的 A点射入磁场区域，并从 O 点射出，粒子射出磁场的速度方向与 x轴的夹角＝30，大小为 v，粒子在磁场内的运动轨 迹为纸面内的一段圆弧，且弧的半径为磁场左右边界间距的 2倍，粒子进入电场后，在电场 力的作用下又由 O点返回磁场区域，经过一段时间后再次离开磁场。已知粒子从 A点射入 到第二次离开磁场所用时间恰好粒子在磁场中做圆周运动的周期。忽略重力的影响。求： （1）粒子经过 A点时的速度方向和 A点到 x轴的距离； （2）匀强电场的大小和方向； （3）粒子从第二次离开磁场到再次进入电场所用的时间。 13. 如图所示，在 oxyz坐标系所在的空间中，可能存在匀强电场 或磁场，也可能两者都存 v0 B MN PQ m,-q L d E x y O O1 在或都不存在。但如果两者都存在，已知磁场平行于 xy平面。现有一质量为 m带正电 q的 点电荷沿 z轴正方向射入此空间中，发现它做速度为 v0的匀速直线运动。若不计重力，试 写出电场和磁场的分布有哪几种可能性。要求对每一种可能性，都要说出其中能存在的关系。 不要求推导或说明理由。 14. 如图所示的区域中，第二象限为垂直纸面向外的匀强磁场，磁感应强度为 B，第一、 第四象限是一个电场强度大小未知的匀强电场，其方向如图。一个质量为 m，电荷量为+q 的带电粒子从 P孔以初速度 v0沿垂直于磁场方向进入匀强磁场中，初速度方向与边界线的 夹角θ=30°，粒子恰好从 y轴上的 C孔垂直于匀强电场射入匀强电场，经过 x轴的 Q点， 已知 OQ=OP，不计粒子的重力，求： （1）粒子从 P运动到 C所用的时间 t； （2）电场强度 E的大小； （3）粒子到达 Q点的动能 Ek。 15.如图所示，MN为纸面内竖直放置的挡板，P、D是纸面内水平方向上的两点，两点距离 PD为 L，D点距挡板的距离 DQ为 L/π．一质量为 m、电量为 q的带正电粒子在纸面内从 P 点开始以 v0的水平初速度向右运动，经过一段时间后在 MN左侧空间加上垂直纸面向里的 磁感应强度为 B的匀强磁场，磁场维持一段时间后撤除，随后粒子再次通过 D点且速度方 向竖直向下．已知挡板足够长，MN左侧空间磁场分布范围足够大．粒子的重力不计．求： （1）粒子在加上磁场前运动的时间 t； （2）满足题设条件的磁感应强度 B的最小值及 B最小时磁场维持的时间 t0的值． 16.如图所示，PR是一长为 L=0.64m的绝缘平板，固定 E B P R L d D C M Q N P D v0 x y z O P x y O Q  060 C B E v0 在水平地面上，挡板 R固定在平板的右端。整个空间有一个平行于 PR的匀强电场 E，在板 的右半部分有一垂直于纸面向里的匀强磁场，磁场的宽度 d=0.32m.一个质量 m=0.50×10-3kg、 带电荷量为 q=5.0×10-2C的小物体，从板的 P端由静止开始向右做匀加速运动，从 D点进入 磁场后恰能做匀速直线运动.当物体碰到挡板 R后被弹回，若在碰撞瞬间撤去电场（不计撤 去电场对原磁场的影响），物体返回时在磁场中仍作匀速运动，离开磁场后做减速运动，停 在 C点，PC=L/4.若物体与平板间的动摩擦因数μ=0.20，g取 10m/s2. ⑴判断电场的方向及物体带正电还是带正电； ⑵求磁感应强度 B的大小； ⑶求物体与挡板碰撞过程中损失的机械能. 参考答案 1. 解:(1)带电粒子在磁场中运动时，洛仑兹力提供向心力 R v mBqv 2 0 (2分) 其转动半径为 qB mv R 0 (2分) 带电粒子在磁场中做匀速圆周运动，连接粒子在磁场区入射点和出射点得弦长为: Rl 3 (2分) 要使圆形匀强磁场区域面积最小，其半径刚好为 l的一半，即: qB mv Rlr 0 2 3 2 3 2 1  (2分) 其面积为 22 2 0 2 2 min 4 3 Bq vm rS    (2分) (2)带电粒子在磁场中轨迹圆弧对应的圆心角为 1200，带电粒子在磁场中运动的时间为 转动周期的 3 1 ， qB mvR Tt 3 2 3 /2 3 1 0   (4分) (3)带电粒子从 O处进入磁场，转过 1200后离开磁场，再做直线运动从 b点射出时 ob 距离: qB mv Rd 03 3  (4分) 2.⑴上金属板带负电。⑵设带电粒子进入电场的初速度为 v，在电场中的侧移是 22 )( 2 1 2 1  l dm qUatd  ，解得 m qU d l 2  。⑶如图所示，设 磁偏转的半径为 R，圆形磁场区域的半径为 r，则 R mBq 2  ， 得 q mU Bd l qB mR 2   ，由几何知识可知 30sinRr  ，磁场 区域的最小面积为 22 2 2 8 dqB mUlrs   。 3. 解：电子的运动轨迹如右图所示 （2分） （若画出类平抛和圆运动轨迹给 1分） （1）电子在电场中做类平抛运动 设电子从 A到 C的时间为 t1 102 tvd  （1分） 2 12 1 atd  （1分） m eEa  （1分） 求出 E = ed mv 2 2 0 （1分） （2）设电子进入磁场时速度为 v，v与 x轴的夹角为θ，则 1tan 0 1  v at  θ = 45° （1分） θ O1 O2 R r θ b x y O R v0 60° l Dθ C v E y x v0 × × × × × × × × × × × × × × × × × × × × A B O θ 求出 02vv  （1分） 电子进入磁场后做匀速圆周运动，洛仑兹力提供向心力 r vmevB 2  （1分） 由图可知 dr 2 （2分） 求出 ed mvB 0 （1分） （3）由抛物线的对称关系，电子在电场中运动的时间为 3t1= 0 6 v d （2分） 电子在磁场中运动的时间 t2= 02 32 4 3 4 3 v d eB mT   （2分） 电子从 A运动到 D的时间 t=3t1+ t2 = 02 )4(3 v d  （2分） 4.解：（1）带电粒子从 C孔进入，与筒壁碰撞 2次再从 C孔射出经历的时间为最短． 由 qE＝1 2 mv2 ……………………………………… 2分 粒子由 C孔进入磁场，在磁场中做匀速圆周运动的速率为 v＝ 2qE m ……………………………………………1分 由 r＝mv qB 即 Rcot30°＝mv qB ………………………………3分 得 B＝1 R 2mE 3q ……………………………………2分 （2）粒子从 A→C的加速度为 a＝qE／md …………………………………………2分 由 d＝at12／2，粒子从 A→C的时间为 t1＝ 2d a =d 2m qE ………………………………… 2分 粒子在磁场中运动的时间为 t2＝T／2＝πm／qB………………………………… 2分 将（1）求得的 B值代入， 得 t2＝πR 3m 2qE ……………………………………… 1分 求得 t＝2t1＋t2＝ m qE （2 2d + 3 2 πR）………………………1分 5.(1): q mEL B Rd 6 2 160sin 0  (2): qB m qE mLtttt 3 722321   6. （1）粒子源发出的粒子，进入加速电场被加速，速度为 v0，根据能的转化和守恒定律得： 2 01 2 1 mvqU  （2分） 要使粒子能沿图中虚线 O2O3进入 PQ、MN之间的区域， 则粒子所受到向上的洛伦兹力与向下的电场力大小相等， BqvqE 0 得到 1 0 B Ev  （2分） 将②式代入①式，得 2 1 2 1 2qB mEU ＝ （1分） （2）粒子从 O3以速度 v0进入 PQ、MN之间的区域，先做匀速直线运动，打到 ab板上，以 大小为 v0的速度垂直于磁场方向运动．粒子将以半径 R在垂直于磁场的平面内作匀速 圆周运动，转动一周后打到 ab板的下部．由于不计板的厚度，所以质子从第一次打到 ab板到第二次打到 ab板后运动的时间为粒子在磁场运动一周的时间，即一个周期 T． 由 R mv qvB 2 0 2  和运动学公式 0 2 v RT   ，得 2 2 qB mT   （2分） 粒子在磁场中共碰到 2块板，做圆周运动所需的时间为 Tt 21  （2分） 粒子进入磁场中，在 v0方向的总位移 s=2Lsin45°，时间为 0 2 v st  （2分） 则 t=t1+t2= E LB qB m 1 2 24   （2分） 粒子做圆周运动的半径为 qBB mE qB mv r 212 0  ， 因此总路程 L BqB mELrs 24222 21   。 7. （1）轨迹如图所示 （2）粒子在加速电场中由动能定理有 2 0vmqU 2 1  ① 粒子在匀强电场中做类平抛运动，设偏转角为 ，有 0 tan yv v   ② yv at ③ qEa m  ④ 0 dt v  ⑤ U= 2 1 Ed ⑥ 由①②③④⑤⑥解得：θ=45º 由几何关系得：带电粒子离开偏转电场速度为 02v 粒子在磁场中运动，由牛顿第二定律有：qvB=mv 2 R 在磁场中偏转的半径为 d qE mv vqE mv qB mvR 2 2 / 2 2 0 0 0  ，由图可知，磁场宽度 L=Rsinθ=d （3）由几何关系可得：带电粒子在偏转电场中距离为 dy 5.01  ， 在磁场中偏转距离为 8.⑴电荷从 A点匀加速运动运动到 x轴的 C点的过程： 位移 s＝AC＝ 2 m …………………（1分） 加速度 m qEa  ＝ 121022  m/s2 …………………（2分） 时间 6102  a st s …………………（2分） ⑵电荷到达 C点的速度为 61022  atv m/s …………………（2分） 速度方向与 x轴正方向成 45°角，在磁场中运动时 由 R mvqvB 2  …………………（2分） 解得 2 2 102 1022 102 1 2 6 8       qB mvR m …………………（2分） 即电荷在磁场中的轨迹半径为 2 2 m …………………（1分） ⑶轨迹圆与 x轴相交的弦长为 12 2  Rx m，所以电荷从坐标原点 O再次进入电场中， 且速度方向与电场方向垂直，电荷在电场中作类平抛运动，运动过程中与 x轴第三次相交 时的坐标为 x3，设运动的时间为 t′，则： tvx 0 3 45cos …………………（2分） 20 3 2 145sin tax  …………………（2分） 解得 t′＝2×10－6s …………………（1分） 83 x m …………………（1分） 即电荷第三次到达 x轴上的点的坐标为（8，0） …………………（1分） 9. （1）t1=L/V0+m/qB0 ddy 414.02) 2 21(2  （2） qL mv B 0 0 2  6L/V0 （3）如图 10. （1）粒子在电场中运动时间为 t， 有： tvL 0 （1分）； 2 2 1 atd  （1分）； m Eqa  （1分）； d UE  （1分）；解得： 2 22 02 qL dmvU  （2分） （2） atv y  （1分）， 0 tan v vy （1分）， cos 0vv  （1分）， sin2 LR  （1分）， R vmqvB 2  （1分），解得： 2 04 qL dmv B  （2 分） （3）画图正确给 2分。 11.（1） m eBrv  （2） eE mr eB mt 2 2   （3） mE erBx 33  + r 12. （1）设磁场左边界与 x轴相交子 D点，与 CO相交于O点， 由几何关系可知，直线 OO 与粒子过 O点的速度 v垂直。在直角三 角形中 DOO  已知 DOO  =300,设磁场左右边界间距为 d，则 OO  =2d。依题意可知，粒子第一次进人磁场的运动轨迹的圆心即 为O点，圆弧轨迹所对的圈心角为 300 ，且 OO 为圆弧的半径 R。 由此可知，粒子自 A点射人磁场的速度与左边界垂直。 A 点到 x轴的距离：AD=R(1－cos300)………………………………① 由洛仑兹力公式、牛顿第二定律及圆周运动的规律，得： R mBq 2vv  ② 联立①②式得： 3(1 ) 2 mvAD qB   …………………………………③ （2）设粒子在磁场中做圆周运动的周期为 T第一次在磁场中飞行的 时间为 t1，有： t1=T/12…………………………………………④ T=2πm/qB………………………………………⑤ 依题意．匀强电场的方向与 x轴正向夹角应为 1500。由几何关系可知，粒子再次从 O点进 人磁场的速度方向与磁场右边界夹角为 600。设粒子第二次在磁场中飞行的圆弧的圆心为 O’’，O’’必定在直线 OC 上。设粒子射出磁场时与磁场右边界文于 P点，则∠OO’’P =1200．设 粒子第二次进人磁场在磁场中运动的时问为 t2有： t2=T/3…………………………………………⑥ 设带电粒子在电场中运动的时间为 t 3，依题意得： t3=T－(t1+t2)…………………………………⑦ 由匀变速运动的规律和牛顿定律可知： ―v=v―at3……………………………………⑧ a=qE/m………………………………………⑨ v0 O MN PQ m,-q L d θ θ P . . . . . . . . . . . . . . . . . . . . 0v x y O Q  060 C B E D F 联立④⑤⑥⑦⑧⑨式可得： E=12Bv/7π……………………………………⑩ 粒子自 P点射出后将沿直线运动。 设其由 P点再次进人电场，由几何关系知：∠O’’P’P =300……⑾ 消 三角形 OPP’为等腰三角形。设粒子在 P、P’两点间运动的时问为 t4，有： t4=PP’/v………………………………………⑿ 又由几何关系知：OP= 3 R………………………………………⒀ 联立②⑿⒀式得：t4= 3 m/qB 13. 以 E和 B分别表示电场强度和磁感强度，有以下几种可能： （1）E＝0，B＝0 （2）E＝0，B≠0。 B的方向与 z轴的方向平行或反平行。B的大小可任意。 （3）E≠0，B≠0。磁场方向可在平行于 xy平面的任何方向。 电场 E 方向平行于 xy平面，并与 B的方向垂直。 当迎着 z轴正方向看时，由 B的方向沿顺时针转 90°后就是 E的方向 E和 B的大小可取满足关系式 0vB E  的任何值。 14. （1）带电粒子在电磁场运动的轨迹如图所示，由图可知，带电粒子在磁场中做匀 速圆周 运动的轨迹为半个圆周（2分） 由 r v mBqv 2 0 0  （1分） 得： qB mv r 0 （1分） 又 T= Bq m v r  22 0  （1分） 得带电粒子在磁场中运动的时间： qB mTt   2 （2分） （2）带电粒子在电场中做类平抛运动，初速度 0v 垂直于电场沿 CF方向，过 Q点 作直线 CF的垂线交 CF于 D，则由几何知识可知，CPO≌CQO≌CDQ，由图可 知： CP= qB mv r 02 2  （1分） 带电粒子从 C运动到 Q沿电场方向的位移为 qB mv rCPOPOQDQSE 0030sin  （2分） 带电粒子从 C运动到 Q沿初速度方向的位移为 qB mv rCPCOCDSv 00 3 330cos 0  （1分） 由类平抛运动规律得： 22 2 1 2 1 t m qEatSE  （1分） tvSv 00  （1分） 联立以上各式解得： 3 2 0Bv E  （2分） （3）由动能定理得： Ek qESmvE  2 02 1 （3分） 联立以上各式解得： 2 06 7 mvEk  （2分） 15. 解：（1）微粒从 P点至第二次通过 D点的运动轨迹如图所示 由图可知在加上磁场前瞬间微粒在 F点（圆和 PQ的切点）． 在 t时间内微粒从 P点匀速运动到 F点，t= PF/v0 ① 由几何关系可知： PF=L＋R ② 又 R=m v0/qB ③ 由①②③式可得： t=L/v0+m/qB （2）微粒在磁场中作匀速圆周运动时，由②式可知：当 R最大时，B最小，在微粒不飞出磁场的情况下，R最大时 有： DQ=2R ， 即 L/π＝2R 可得 B的最小值为： Bmin=2πmv0 /qL 微粒在磁场中做圆周运动，故有 t0=（n＋3/4）T ，n＝0，1，2，3， 又：T=2πm/qB 即可得： t0=（n＋3/4）L/v0 ,( n＝0，1，2，3，…… ) 16. (1)物体由静止开始向右做匀加速运动，证明电场力向右且大于摩擦力.进入磁场后做匀速 直线运动，说明它受的摩擦力增大，证明它受的洛仑兹力方向向下.由左手定则判断，物体 带负电.…………………………2分 物体带负电而所受电场力向右，证明电场方向向左.…………………………2分 (2)设物体被挡板弹回后做匀速直线运动的速度为 v2，从离开磁场到停在 C点的过程中， 根据动能定理有   mg L mv 4 0 1 2 2 2…………………………2分 解得v m s2 080 . / …………………………1分 物体在磁场中向左做匀速直线运动，受力平衡 mg qv B 2 ………………2分 解得B T T 0125 013. . …………………………1分 （3）设从 D点进入磁场时的速度为 v1，根据动能定理有： qE L mg L mv1 2 1 2 1 2 1 2  …………………………2分 物体从 到 做匀速直线运动受力平衡：D R qE mg qv B ( )1 ………………2分 解得v m s1 16 . / …………………………1分 小物体撞击挡板损失的机械能为：E mv mv  1 2 1 21 2 2 2……………………2分 F M Q N P D v0 解得   4 8 10 4. J …………………………1分