高中物理第一章电磁感应3法拉第电磁感应定律课件-63张 63页

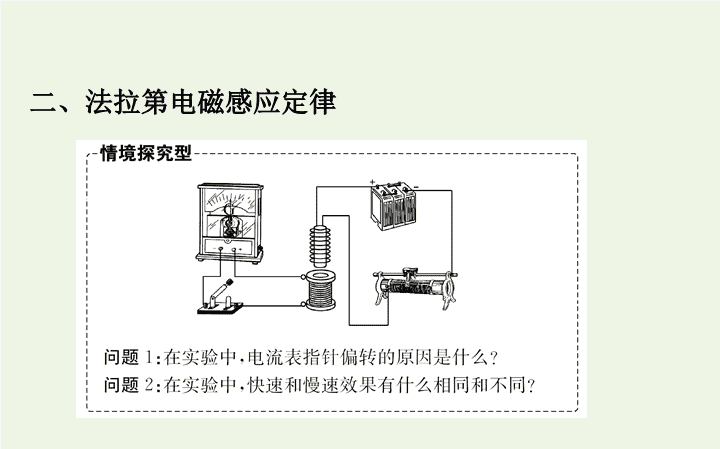
　 3. 法拉第电磁感应定律 　 一、感应电动势 1. 感应电动势 : 由 _________ 产生的电动势。 2. 在电磁感应现象中 , 回路断开时 , 虽然没有感应电 流 , 但 ___________ 依然存在。 电磁感应 感应电动势 二、法拉第电磁感应定律 1. 内容 : 电路中感应电动势的大小 , 跟穿过这个电路的 磁通量的 _______ 成正比。 2. 公式 :E=_____ 。若闭合导体回路是一个匝数为 n 的线 圈 , 则 E=_____ 。 3. 单位 : 在国际单位制中 ,E 的单位是 _____(V),Φ 的单 位是 _____(Wb),t 的单位是 ___(s) 。 变化率 伏特 韦伯 秒 三、导线切割磁感线产生的感应电动势 1. 垂直切割 : 导体棒垂直于磁场运动 ,B 、 L 、 v 两两垂 直时 , 如图甲 ,E=____ 。 BLv 2. 不垂直切割 : 导线不垂直切割磁感线时 , 即 v 与 B 有一 夹角 α, 如图乙所示。此时可将导线的速度 v 向垂直于 磁感线和平行于磁感线两个方向分解 , 则使导线切割磁 感线的分速度为 v ⊥ = _______ , 导线产生的感应电动势为 E= _____ = _________ 。 vsinα BLv ⊥ BLvsinα 【 思考辨析 】 (1) 电路中的磁通量越大 , 感应电动势就越大。 ( 　　 ) (2) 电路中的磁通量变化量越大 , 感应电动势就越大。 ( 　　 ) (3) 电路中的磁通量变化率越大 , 感应电动势就越大。 ( 　　 ) (4) 对于 E=BLv 中的 B 、 L 、 v 三者必须相互垂直。 ( 　　 ) (5) 导体棒在磁场中运动速度越大 , 产生的感应电动势一定越大。 ( 　　 ) (6) 当 B 、 L 、 v 三者大小、方向均不变时 , 在 Δt 时间内的平均感应电动势和它在任意时刻产生的瞬时感应电动势相同。 ( 　　 ) 提示 : (1)× 。不一定。磁通量越大 , 磁通量的变化率不一定大 , 所以感应电动势不一定大。 (2)× 。不一定。磁通量的变化量大 , 若时间很长 , 磁通量的变化率不一定大 , 感应电动势不一定大。 (3)√ 。电路中的磁通量变化率越大 , 感应电动势就越大 , 说法正确。 (4)√ 。对于 E=BLv 中的 B 、 L 、 v 三者必须相互垂直。 (5)× 。如果导体棒在磁场中运动速度与磁场平行 , 产生的感应电动势为零。 (6)√ 。当 B 、 L 、 v 三者大小、方向均不变时 , 它在任意时刻产生的瞬时感应电动势保持不变 , 所以在 Δt 时间内的平均感应电动势和它在任意时刻产生的瞬时感应电动势相同。 一　磁通量 Φ 、磁通量的变化量 ΔΦ 及磁通量的变化 率 的区别 【 典例 】 一个 200 匝、面积为 20 cm 2 的线圈 , 放在匀强 磁场中 , 磁场的方向与线圈平面成 30° 夹角 , 磁感应强 度在 0.05 s 内由 0.1 T 增加到 0.5 T 。在此过程中 , 穿 过线圈的磁通量的变化量是多少 ? 磁通量的平均变化率 是多少 ? 【 解题探究 】 (1) 磁通量的变化量 _______________ 。 (2) 磁通量的变化率为 ______ 。 ΔΦ=ΔBSsinθ 【 正确解答 】 磁通量的变化量为 ΔΦ=ΔB · S · sin30° =(0.5-0.1)×20×10 -4 ×0.5 Wb =4×10 -4 Wb 磁通量的平均变化率为 = Wb/s =8×10 -3 Wb/s 答案 : 4×10 -4 Wb 　 8×10 -3 Wb/s 【 核心归纳 】 1. 磁通量变化量 ΔΦ 的计算方法 : (1) 磁通量的变化是由面积变化引起的 ,ΔΦ=B·ΔS 。 (2) 磁通量的变化是由磁场变化引起的 ,ΔΦ=ΔB·S 。 (3) 磁通量的变化是由面积和磁感应强度间的角度变化引起的 , 根据定义求 ΔΦ=Φ 2 -Φ 1 。 2.Φ 、 ΔΦ 、 的区别 : 物理量 单　位 物理意义 计算公式 磁通量 Φ Wb 表示某时刻或某位置时穿过某一面积的磁感线条数的多少 Φ=B·S ⊥ 磁通量的 变化量 ΔΦ Wb 表示在某一过程中穿过某一面积的磁通量变化的多少 ΔΦ=Φ 2 -Φ 1 物理量 单　位 物理意义 计算公式 磁通量的 变化率 = Wb/s 表示穿过某一面积的磁通量变化的快慢 【 特别提醒 】 (1)Φ 、 ΔΦ 、 均与线圈匝数无关。 (2) 磁通量和磁通量的变化率的大小没有直接关系 ,Φ 很大时 , 可能很小 , 也可能很大 ;Φ=0 时 , 可能不 为零。 【 过关训练 】 1. 下列说法正确的是 ( 　　 ) A. 线圈中磁通量变化越大 , 线圈中产生的感应电动势一定越大 B. 线圈中磁通量越大 , 线圈中产生的感应电动势一定越大 C. 线圈处在磁场越强的位置 , 线圈中产生的感应电动势一定越大 D. 线圈中磁通量变化得越快 , 线圈中产生的感应电动势越大 【 解析 】 选 D 。线圈中产生的感应电动势 E=n , 即 E 与 成正比 , 与 Φ 或 ΔΦ 的大小无直接关系。磁通量变化 越快 , 即 越大 , 产生的感应电动势越大 , 故只有 D 正确。 2. 穿过一个内阻为 1 Ω 的 10 匝闭合线圈的磁通量每秒均匀减少 2 Wb, 则线圈中 ( 　　 ) A. 感应电动势每秒增加 2 V B. 感应电动势每秒减少 2 V C. 磁通量的变化率为 2 Wb/s D. 感应电流为 2 A 【 解析 】 选 C 。磁通量的变化率 =2 Wb/s,C 正确。 由 E=n 得 E=10×2 V=20 V, 感应电动势不变 ,A 、 B 错 误。由 I= 得 I= A=20 A,D 错误。 二　对电磁感应定律的理解 【 典例 】 如图甲所示 , 一个圆形线圈的匝数 n=1 000, 线圈面积 S=200 cm 2 , 线圈的电阻 r=1 Ω, 线圈外接一个阻值 R=4 Ω 的电阻 , 把线圈放入一方向垂直线圈平面向里的匀强磁场中 , 磁感应强度随时间的变化规律如图乙所示。求 : (1) 前 4 s 内的感应电动势。 (2) 前 4 s 内通过 R 的电荷量。 【 正确解答 】 (1) 由图像可知前 4 s 内磁感应强度 B 的 变化率 = T/s=0.05 T/s 4 s 内的平均感应电动势 E=nS =1 000×0.02×0.05 V=1 V 。 (2) 电路中的平均感应电流 = ,q= t, 又因为 E=n , 所以 q=n =1 000× C=0.8 C 。 答案 : (1)1 V 　 (2)0.8 C 【 核心归纳 】 1. 感应电动势 E=n 的两种基本形式 : (1) 当垂直于磁场方向的线圈面积 S 不变 , 磁感应强度 B 发生变化时 ,ΔΦ=ΔB·S, 则 E=n S, 其中 叫磁感 应强度 B 的变化率。 (2) 当磁感应强度 B 不变 , 垂直于磁场方向的线圈面积 S 发生变化时 ,ΔΦ=B·ΔS, 则 E=nB 。 2.E=n 的意义 : E=n 求出的是 Δt 时间内的平均感应电动势。 3. 电磁感应中电荷量的求解思路 : (1) 产生恒定电流时 : 在电磁感应现象中产生了感应电流 , 就有电荷的定向移动 ,Δt 时间内通过电路某一截面的电荷量 q=IΔt 。 (2) 不是恒定电流时 : 计算电量必须用平均感应电流和 平均感应电动势 , 平均感应电动势一般用法拉第电磁感 应定律求解 , 因此 q= = Δt=n Δt=n , q 与 ΔΦ 成正比 , 与时间无关 , 式中 R 为回路的总电阻。 【 过关训练 】 1. ( 多选 ) 电流流过线圈会产生磁场 , 其 他未通电的线圈靠近该磁场就会产生电 流。无线充电就应用了这种称为“电磁 感应”的物理现象。将可与磁场振动共振的线圈排列 起来 , 可以延长供电距离 , 如图所示。下列说法正确的 是 ( 　　 ) A. 若 A 线圈中输入电流 ,B 线圈中就会产生感应电动势 B. 只有 A 线圈中输入变化的电流 ,B 线圈中才会产生感应电动势 C.A 中电流越大 ,B 中感应电动势越大 D.A 中电流变化越快 ,B 中感应电动势越大 【 解析 】 选 B 、 D 。根据产生感应电动势的条件 , 只有处于磁场中的磁通量发生变化 ,B 线圈才能产生感应电动势 , 故 A 错误 ,B 正确 ; 根据法拉第电磁感应定律 , 感应电动势的大小取决于磁通量的变化率 , 故 C 错误 ,D 正确。 2. 如图所示 , 半径为 r 的金属环绕通过其 直径的轴 OO′ 以角速度 ω 做匀速转动 , 匀强磁场的磁感应强度为 B 。从金属环 的平面与磁场方向重合时开始计时 , 在转过 30° 角的过 程中 , 环中产生的电动势的平均值为 ( 　　 ) A.2Bωr 2 　　 B.2 Bωr 2 　　 C.3Bωr 2 　　 D.3 Bωr 2 【 解析 】 选 C 。开始时 ,Φ 1 =0, 金属环转过 30° 时 , Φ 2 =BS sin30°= Bπr 2 , 故 ΔΦ=Φ 2 -Φ 1 = Δt= = = 。根据 E= , 环中电动势平均值 E= 3Bωr 2 , 故选 C 。 【 补偿训练 】 一个面积 S=4×10 -2 m 2 、匝数 n=100 匝的 线圈 , 放在匀强磁场中 , 磁场方向垂直于 线圈平面 , 磁感应强度 B 随时间 t 变化的 规律如图所示 , 则下列判断正确的是 ( 　　 ) A. 在开始的 2 s 内穿过线圈的磁通量变化率等于 -0.08 Wb/s B. 在开始的 2 s 内穿过线圈的磁通量的变化量等于零 C. 在开始的 2 s 内线圈中产生的感应电动势大小等于 0.08 V D. 在第 3 s 末线圈中的感应电动势等于零 【 解析 】 选 A 。由 = ·S 得 ,A 项正确。在开始的 2 s 内线圈中产生的感应电动势大小为 E=n =8 V, 所 以 B 、 C 项错误。第 3 s 末线圈中的感应电动势不等于零 , 所以 D 错误。 三　导体切割磁感线产生的感应电动势 【 典例 】 如图所示 , 在磁感应强度为 0.2 T 的匀强磁场中 , 有一长为 0.5 m 、电阻为 1.0 Ω 的导体 AB 在金属框架上以 10 m/s 的速度向右滑 动 ,R 1 =R 2 =2.0 Ω, 其他电阻不计 , 求流过 R 1 的电流 I 1 。 【 规范解答 】 AB 切割磁感线相当于电源 , E AB =B l v=0.2×0.5×10 V=1 V 由闭合电路欧姆定律得 I= ,R 1 、 R 2 并联 , 由并联电 路电阻关系得 = + , 解得 :R= =1.0 Ω, I AB =I=0.5 A 因为 R 1 =R 2 , 所以流过 R 1 的电流为 I 1 = =0.25 A 。 答案 : 0.25 A 【 核心归纳 】 1. 电磁感应中电路问题的分析方法 : (1) 分析产生感应电动势的原因 , 确定感应电动势存在于何处。 (2) 明确电路结构 , 分清内、外电路 : 产生感应电动势的那部分导体相当于电源 , 而没有产生感应电动势的另一部分导体相当于外电路。 (3) 画出等效电路图。 (4) 计算感应电动势的大小。①如果是磁场或回路有效 面积变化 , 由 E=n 计算 ;② 如果是导体切割磁感线 , 由 E=B l vsinθ 计算。 (5) 根据欧姆定律和串、并联电路的特点进行电路的分 析与计算。 E=n E=BLvsinθ 区别 研究 对象 某个回路 回路中做切割磁感线运动的那部分导体 研究 内容 (1) 求的是 Δt 时间内的平均感应电动势 ,E 与某段时间或某个过程对应 (2) 当 Δt→0 时 ,E 为瞬时感应电动势 (1) 若 v 为瞬时速度 , 公式求的是瞬时感应电动势 (2) 若 v 为平均速度 , 公式求的是平均感应电动势 (3) 当 B 、 L 、 v 三者均不变时 , 平均感应电动势与瞬时感应电动势相等 2. 公式 E=n 与 E=BLvsinθ 的区别与联系。 E=n E=n E=BLvsinθ 区别 适用 范围 对任何电路普遍适用 只适用于导体切割磁感线 运动的情况 联系 (1)E=BLvsinθ 可由 E=n 在一定条件 下推导出来 (2) 整个回路的感应电动势为零时 , 回路 中某段导体的感应电动势不一定为零 3. 平动切割 : (1) 计算公式 :E=BLv 。 (2) 理解 E=BLv 的“三性”。 ①正交性 : 该公式可看成法拉第电磁感应定律的一个推 论 , 除了磁场是匀强磁场外 , 还需要 B 、 L 、 v 三个量方向 相互垂直时 ,E=BLv; 如有不垂直的情况 , 应通过正交分 解取其垂直分量代入 , 当有任意两个量的方向平行时 ,E=0 。 ②瞬时对应性 : 通常用来求导体运动速度为 v 时的瞬时电动势 , 若 v 为平均速度 , 则 E 为平均电动势。 ③有效性 : 式中的 L 应理解为导体切割磁感线时的有效长度。如图所示 , 导体切割磁感线的情况应取与 B 和 v 垂直的等效直线长度 , 即等于 a 、 b 连线的长度。 4. 转动切割 : (1) 如图所示 , 在匀强磁场 B 中 , 有一长为 L 的导体棒 , 以其一端为轴 , 在垂直于磁场 的平面内以角速度 ω 匀速转动 , 则导体棒 两端所产生的感应电动势 E= BL 2 ω 。 (2) 推导。 方法一 : 设导体棒在 Δt 时间内扫过面积 ΔS, 则 ΔS= L·L·ω·Δt= L 2 ω·Δt E= = = BL 2 ω 方法二 : 整根导体棒的平均切割速度为 = = , 由公式 E=BL 得 , 导体棒转动切割磁 感线产生的感应电动势为 E=BL = BL 2 ω 。 【 特别提醒 】 (1) 切割磁感线的导体中产生感应电动势 , 该部分导体等效为电源 , 电路中的其余部分等效为外电路。 (2) 对于一个闭合电路 , 关键要明确电路的连接结构 , 分清哪部分相当于电源 , 哪些组成外电路 , 以及外电路中的串、并联关系。 (3) 一般高中阶段只考查 B 、 L 、 v 互相垂直的情况 , 即 sinθ=1 的情况。 【 过关训练 】 1. 如图所示 ,MN 、 PQ 为两条平行的水平放置的金属导轨 , 左端接有定值电阻 R, 金属棒 ab 斜放在两导轨之间 , 与导轨接触良好 ,ab=L 。磁感应强度为 B 的匀强磁场垂直于导轨平面 , 设金属棒与两导轨间夹角为 60°, 以速度 v 水平向右匀速运动 , 不计导轨和棒的电阻 , 则流过金属棒中的电流为 ( 　　 ) A.I= 　　 B.I= 　　 C.I= 　　 D.I= 【 解析 】 选 B 。导体棒切割磁感线的有效长度为 : L·sin60°= L, 故感应电动势 E=Bv , 由闭合 电路欧姆定律得 I= , 故选项 B 正确。 2. 如图所示 , 在磁感应强度为 B 的匀强磁场中 , 有半径为 r 的光滑半圆形导体框架 ,OC 为一能绕 O 在框架上滑动的导体棒 ,OC 之间连一个电阻 R, 导体框架与导体棒的电阻均不计 , 若要使 OC 能以角速度 ω 匀速转动 ( 未离开框架 ), 则电路中的电流大小是 A. 　　　 B. 　　　 C. 　　　 D. 【 解析 】 选 B 。导体棒 OC 转动产生的电动势为 , 由 I= 得回路的电流为 , 故选 B 。 【 补偿训练 】 1. 如图所示 , 平行导轨间有一矩形的匀强磁场区域 , 细金属棒 PQ 沿导轨从 MN 处匀速运动到 M′N′ 的过程中 , 棒上感应电动势 E 随时间 t 变化的图示 , 可能正确的是 ( 　　 ) 【 解析 】 选 A 。金属棒在到达匀强磁场之前 , 闭合回路的磁通量为零 , 不产生感应电动势。金属棒在磁场中运动时 , 匀速切割磁感线 , 并且切割的有效长度也不变 , 由公式 E=BLv 知 , 此段时间内感应电动势为定值。金属棒离开磁场后 , 闭合回路的磁通量变为零 , 无感应电动势产生 , 选项 A 正确。 2. 如图所示 , 在竖直向下的匀强磁场中 , 将一水平放置的金属棒 ab 以水平初速度 v 0 抛出 , 设在整个过程中棒的方向不变且不计空气阻力 , 则在金属棒运动过程中产生的感应电动势大小变化情况是 ( 　　 ) A. 越来越大　　　　　 B. 越来越小 C. 保持不变 D. 无法判断 【 解析 】 选 C 。棒 ab 水平抛出后 , 其速度越来越大 , 但只有水平分速度 v 0 切割磁感线产生电动势 , 故 E=B l v 0 保持不变。 【 拓展例题 】 考查内容 : 电磁感应中电荷量的求解方法 【 典例 】 圆形线圈处于磁感应强度为 B 的匀强磁场中 , 磁场的方向垂直于线圈平面 , 线圈半径为 r, 电阻为 R, 若用时间 Δt 把线圈从磁场中拉出来和原地使线圈翻转 180°, 则通过线圈导线截面的电量分别为多少 ? 【 正确解答 】 把线圈从磁场中拉出时 : q= Δt= Δt=n Δt=n = 原地翻转 180° 时 , 磁通量变化 ΔΦ′=2BS=2Bπr 2 , q′= ′ Δ t′= Δ t′=n Δ t′=n = 答案 :