2020版高中物理 第二章 能的转化与守恒 第3节 能量守恒定律试题 鲁科版必修2 7页

第3节　能量守恒定律 ‎【二维选题表】‎ 物理观念 科学思维 科学探究 科学态度与责任 机械能守恒定律的理解和 应用 ‎1(易),2(易),‎ ‎3(易),4(易),‎ ‎5(中),‎ ‎11(中),‎ ‎12(中),‎ ‎13(中),‎ ‎14(难)‎ 能量守恒定律的 理解 ‎6(易),7(易),‎ ‎8(中)‎ ‎6(易)‎ 实验:验证机械能 守恒 ‎9(易),‎ ‎10(中)‎ 基础训练 ‎1.在下列物理现象或者物理过程中,机械能守恒的是(　D　)‎ A.匀速下落的降落伞 B.石块在空中做平抛运动(考虑空气阻力)‎ C.沿斜面匀速上行的汽车 D.细绳拴着的小球在光滑的水平桌面上做匀速圆周运动 解析:匀速下落的降落伞受重力和阻力作用,阻力做负功,降落伞的机械能减少,沿斜面匀速上行的汽车,动能不变,重力势能增加,机械能增加,选项A,C错误.选项B中除重力做功外,空气阻力也做功,石块机械能不守恒;选项D中小球机械能不变,故选D.‎ ‎2.(2016·福建邵武七中期中)如图所示,在水平台面上的A点,一个质量为m的物体以初速度v0抛出,不计空气阻力,以水平地面为零势能面,则当它到达B点时的机械能为(　B　)‎ A.m+mgh B.m+mgH C.mgH-mgh D.m+mg(H-h)‎ 解析:物体在运动过程中机械能守恒,故在B处机械能与在A处机械能相等,故B正确.‎ ‎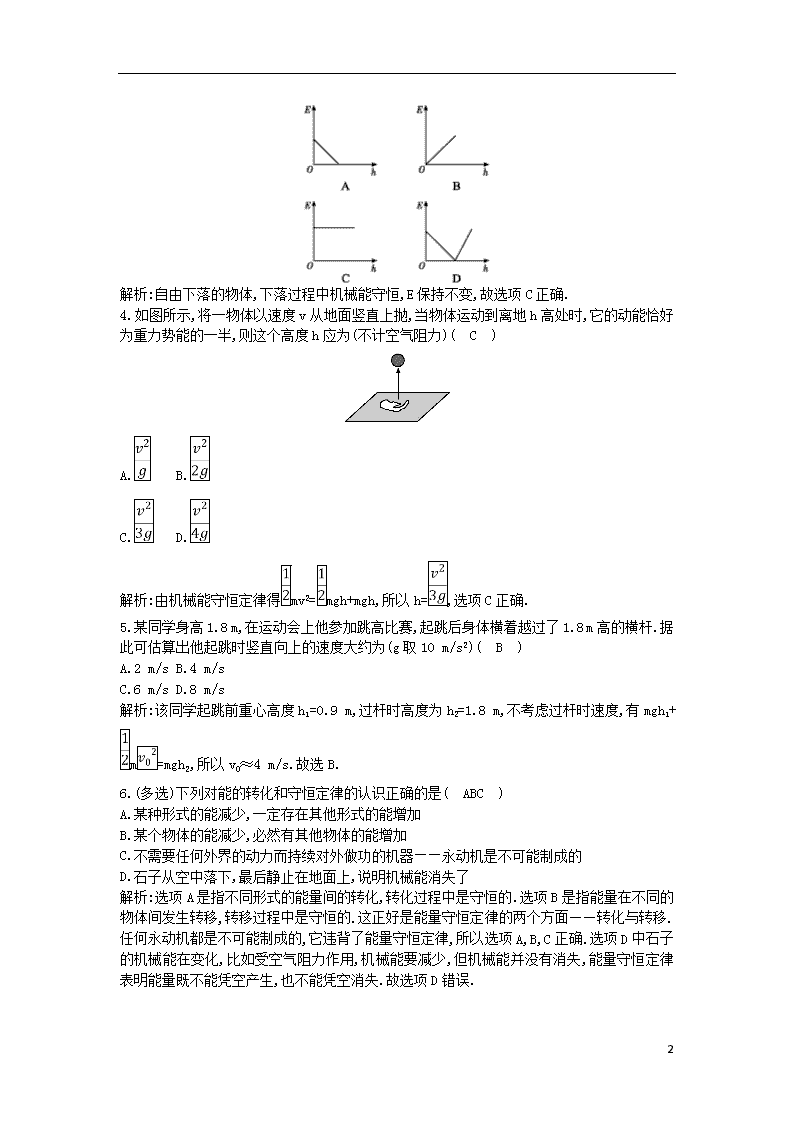3.从高处自由下落的物体,它的机械能E随高度变化的规律由哪个图象来表示(　C　)‎ 7‎ 解析:自由下落的物体,下落过程中机械能守恒,E保持不变,故选项C正确.‎ ‎4. 如图所示,将一物体以速度v从地面竖直上抛,当物体运动到离地h高处时,它的动能恰好为重力势能的一半,则这个高度h应为(不计空气阻力)(　C　)‎ A. B. ‎ C. D.‎ 解析:由机械能守恒定律得mv2=mgh+mgh,所以h=,选项C正确.‎ ‎5.某同学身高‎1.8 m,在运动会上他参加跳高比赛,起跳后身体横着越过了‎1.8 m高的横杆.据此可估算出他起跳时竖直向上的速度大约为(g取‎10 m/s2)(　B　)‎ A‎.2 m/s B‎.4 m/s ‎ C‎.6 m/s D‎.8 m/s 解析:该同学起跳前重心高度h1=‎0.9 m,过杆时高度为h2=‎1.8 m,不考虑过杆时速度,有mgh1+m=mgh2,所以v0≈‎4 m/s.故选B.‎ ‎6.(多选)下列对能的转化和守恒定律的认识正确的是(　ABC　)‎ A.某种形式的能减少,一定存在其他形式的能增加 B.某个物体的能减少,必然有其他物体的能增加 C.不需要任何外界的动力而持续对外做功的机器——永动机是不可能制成的 D.石子从空中落下,最后静止在地面上,说明机械能消失了 解析:选项A是指不同形式的能量间的转化,转化过程中是守恒的.选项B是指能量在不同的物体间发生转移,转移过程中是守恒的.这正好是能量守恒定律的两个方面——转化与转移.任何永动机都是不可能制成的,它违背了能量守恒定律,所以选项A,B,C正确.选项D中石子的机械能在变化,比如受空气阻力作用,机械能要减少,但机械能并没有消失,能量守恒定律表明能量既不能凭空产生,也不能凭空消失.故选项D错误.‎ 7‎ ‎7. (多选)一物体获得一定初速度后,沿着一粗糙斜面上滑,在上滑过程中,物体和斜面组成的系统(　BD　)‎ A.机械能守恒 ‎ B.总能量守恒 C.机械能和内能增加 ‎ D.机械能减少,内能增加 解析:物体沿斜面上滑的过程中,有摩擦力对物体做负功,所以物体的机械能减少,由能量转化和守恒定律知,内能应增加,能的总量不变.选项B,D正确.‎ ‎8.在奥运比赛项目中,高台跳水是我国运动员的强项.质量为m的跳水运动员进入水中后受到水的阻力而做减速运动,设水对他的阻力大小恒为f,那么在他进入水中后降低高度为h的过程中,下列说法正确的是(g为当地的重力加速度)(　D　)‎ A.他的动能减少了mgh B.他的重力势能增加了mgh C.他的机械能增加了fh D.他的机械能减少了fh 解析:下降过程中重力做正功,重力势能减少了mgh,选项B错误;他的动能的变化量等于合外力做的功,即ΔEk=mgh-fh,故选项A错误;因重力之外的力做功等于机械能的变化,降低过程f做负功,机械能减少fh,选项D正确.‎ ‎9. 如图所示为用打点计时器验证机械能守恒定律的实验装置.关于这一实验,下列说法中正确的是(　B　)‎ A.打点计时器应接低压直流电源 B.应先接通电源打点,后释放纸带 C.需使用秒表测出重物下落的时间 D.测量重物下落高度时刻度尺必须竖直放置 解析:打点计时器应接低压交流电源,选项A错误;使用时先接通电源,再释放纸带,选项B正确;重物下落时间由打点计时器打出的纸带直接得出,选项C错误;物体下落高度可通过纸带用刻度尺测量得到,选项D错误.‎ ‎10.(2016·江苏卷,11)某同学用如图(甲)所示的装置验证机械能守恒定律.一根细线系住钢球,悬挂在铁架台上,钢球静止于A点,光电门固定在A的正下方.在钢球底部竖直地粘住一片宽度为d的遮光条.将钢球拉至不同位置由静止释放,遮光条经过光电门的挡光时间t可由计时器测出,取v=‎ 7‎ 作为钢球经过A点时的速度.记录钢球每次下落的高度h和计时器示数t,计算并比较钢球在释放点和A点之间的势能变化大小ΔEp与动能变化大小ΔEk,就能验证机械能是否守恒.‎ ‎(1)用ΔEp=mgh计算钢球重力势能变化的大小,式中钢球下落高度h应测量释放时的钢球球心到　　　　之间的竖直距离. ‎ A.钢球在A点时的顶端 B.钢球在A点时的球心 C.钢球在A点时的底端 ‎(2)用ΔEk=mv2计算钢球动能变化的大小,用刻度尺测量遮光条宽度,示数如图(乙)所示,其读数为　　　　 cm.某次测量中,计时器的示数为0.010 0 s,则钢球的速度为v=　　　　 m/s. ‎ ‎(3)下表为该同学的实验结果:‎ ΔEp(×10-2 J)‎ ‎4.892‎ ‎9.786‎ ‎14.69‎ ‎19.59‎ ‎29.38‎ ΔEk(×10-2 J)‎ ‎5.04‎ ‎10.1‎ ‎15.1‎ ‎20.0‎ ‎29.8‎ 他发现表中的ΔEp与ΔEk之间存在差异,认为这是由于空气阻力造成的.你是否同意他的观点?请说明理由.‎ ‎(4)请你提出一条减小上述差异的改进建议.‎ 解析:(1)钢球下落的高度为初末位置球心间的竖直距离,所以选B.(2)由图知读数为‎1.50 cm(1.49～1.51都算对),钢球的速度为v=,代入数据解得v=‎1.50 m/s(1.49～1.51都算对).(3)若是空气阻力造成的,则ΔEk应小于ΔEp,根据表格数据知不是空气阻力造成的.(4)钢球经过A点时,光电门的位置低于球心的位置,故实验中测得的钢球速度大于钢球在A点的实际速度.遮光条与钢球运动的角速度相等,由v=ω·r知,ω一定时,v与r成正比,故分别测出光电门和球心到悬点的距离L和l,即可折算出钢球经过A点时的速度v′=·v.‎ 7‎ 答案:(1)B　(2)1.50(1.49～1.51都算对)　1.50(1.49～1.51都算对)　(3)见解析　(4)分别测出光电门和球心到悬点的长度L和l,计算ΔEk时,将v折算成钢球的速度v′=v 素养提升 ‎11. (2016·邵武七中期中)如图所示,一根轻弹簧下端固定,竖立在水平面上,其正上方A位置有一小球.小球从静止开始下落,在B位置接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零,在小球下降阶段中,下列说法正确的是(　C　)‎ A.在B位置小球动能最大 B.从A→C位置小球重力势能的减少量等于小球动能的增加量 C.从A→D位置小球动能先增大后减小 D.从B→D位置小球动能的减少量等于弹簧弹性势能的增加量 解析:小球从B至C过程,重力大于弹力,合力向下,小球加速,故在C点动能最大,故A错误;小球下降过程中,重力和弹簧弹力做功,小球和弹簧系统机械能守恒;从A→C位置小球重力势能的减少量等于小球动能增加量和弹簧弹性势能增加量之和,故B错误;从A到D小球下降过程中,在C处动能最大,故C正确;从B→D位置,小球动能减少量与重力势能的减少量之和等于弹簧弹性势能的增加量,故D错误.‎ ‎12. 在跳水比赛中,有一个单项是“‎3 m跳板”,其比赛过程可简化为:运动员走上跳板,跳板被压到最低点,跳板又将运动员竖直向上弹到最高点,运动员做自由落体运动,竖直落入水中.将运动员视为质点,运动员质量m=‎60 kg,g=‎10 m/s2,最高点A、跳板的水平点B、最低点C和水面之间的竖直距离如图所示.求:‎ ‎(1)跳板被压到最低点C时具有的弹性势能多大?‎ ‎(2)运动员入水前速度大小.(可以用根号表示结果)‎ 解析:(1)运动员由C点运动到A点时,跳板的弹性势能转化为运动员的重力势能,则 Ep=mghAC=60×10×(1.5+0.5) J=1 200 J.‎ ‎(2)运动员由A点开始做自由落体运动,机械能守恒,‎ 则mghA=mv2‎ 所以入水前的速度为 v== m/s=‎3‎‎ m/s.‎ 答案:(1)1 200 J　(2)‎3 m/s 7‎ ‎13. 如图所示,在竖直平面内,由斜面和圆形轨道分别与水平面相切连接而成的光滑轨道,圆形轨道的半径为R.质量为m的小物块从斜面上距水平面高为h=2.5R的A点由静止开始下滑,物块通过轨道连接处的B,C点时,无机械能损失.求: ‎ ‎(1)小物块通过B点时速度vB的大小;‎ ‎(2)小物块通过圆形轨道的最高点D的速度vD的大小.‎ 解析:(1)在AB段由机械能守恒定律得 mgh=m 解得vB=.‎ ‎(2)在BD段由机械能守恒定律得 m=mg·2R+m 解得vD=.‎ 答案:(1)　(2)‎ ‎14. 如图所示,物块A的质量为‎2m,物块B的质量是m,A,B都可看做质点,A,B用细线通过滑轮连接,物块A与物块B到地面的距离都是h=‎15 m.现将物块B下方的细线剪断,若物块B距滑轮足够远且不计一切阻力.求:‎ ‎(1)物块A落地前瞬间的速度v;‎ ‎(2)物块A落地后物块B继续上升的最大高度H.(重力加速度取g=‎ ‎10 m‎/s2,空气阻力不计)‎ 解析:(1)A落地前瞬间A,B具有相同的速率,选择地面为零势能面,‎ 由机械能守恒定律得:2mgh+mgh=mg×2h+mv2‎ ‎(也可用动能定理)‎ 代入数据得v=‎10 m/s.‎ ‎(2)对B用动能定理得:mv2=mgH 7‎ 代入数据得H=‎5 m.‎ 答案:(1)‎10 m/s　(2)‎‎5 m 7‎