2019-2020学年高中物理第3章磁场模块备考方略课件 人教版选修3-1 73页

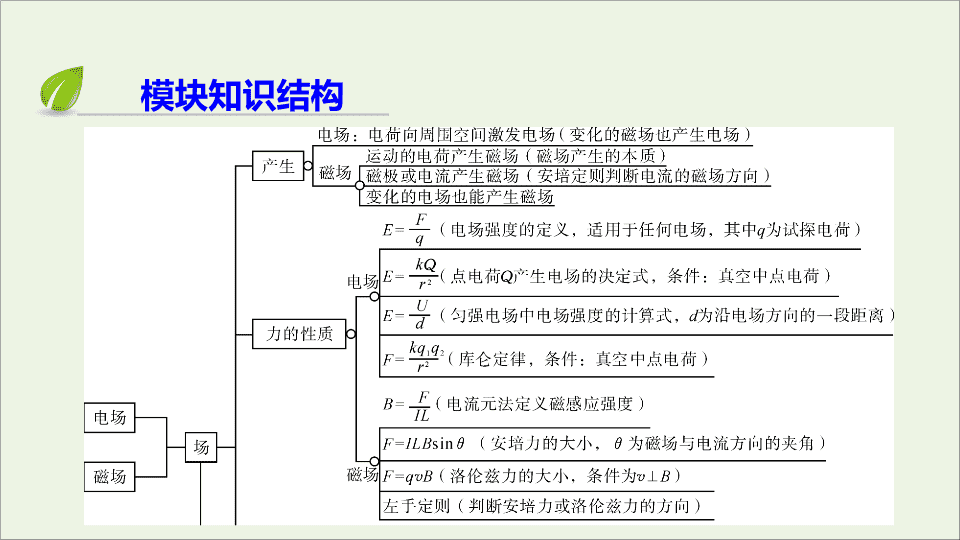
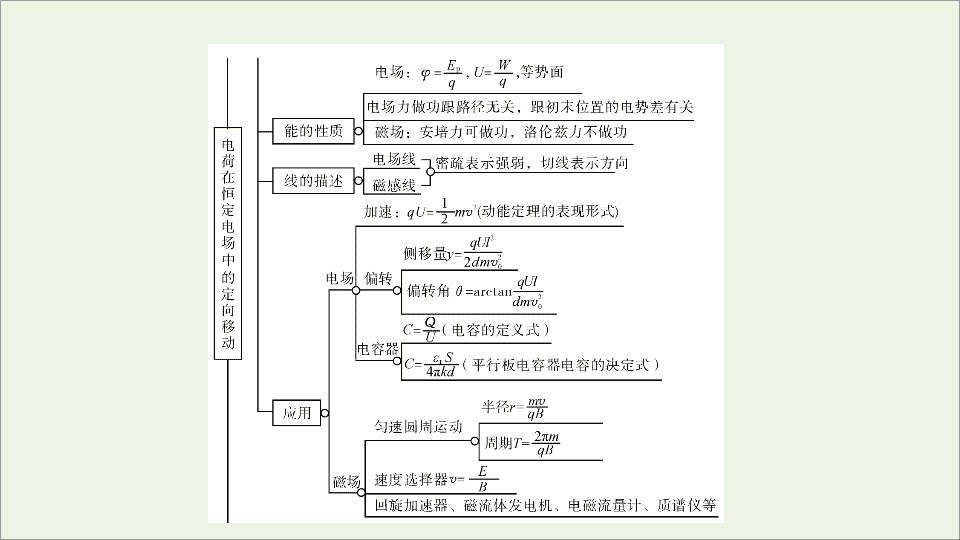
模块备考方略 模块知识结构 几种常见的图象的特点及规律 模块题型总结 题型一　带电粒子在电场中运动的图象问题 v － t 图象 根据 v － t 图象中速度变化、斜率确定电荷所受合力的方向与合力大小的变化，确定电场的方向、电势高低及电势能变化 φ － x 图象 ① 电场强度的大小等于 φ － x 图线的斜率大小，电场强度为零处， φ － x 图线存在极值，其切线的斜率为零； ② 在 φ － x 图象中可以直接判断各点电势的高低，并可根据电势高低关系确定电场强度的方向； ③ 在 φ － x 图象中分析电荷移动时，电势能的变化可用 W AB ＝ qU AB ，进而分析 W AB 的正负，然后做出判断 E － t 图象 根据题中给出的 E － t 图象，确定 E 的方向，再在草纸上画出对应电场线的方向，根据 E 的大小变化，确定电场的强弱分布 E － x 图象 ① 反映了电场强度随位移变化的规律； ② E >0 表示场强沿 x 轴正方向， E <0 表示场强沿 x 轴负方向； ③ 图线与 x 轴围成的 “ 面积 ” 表示电势差， “ 面积 ” 大小表示电势差大小，两点的电势高低根据电场方向判定 【考题 1 】 静电场方向平行于 x 轴，其电势 φ 随 x 的分布可简化为如图所示的折线，图中 φ 0 和 d 为已知量．一个带负电的粒子在电场中以 x ＝ 0 为中心、沿 x 轴方向做周期性运动．已知该粒子质量为 m 、电量为－ q ，其动能与电势能之和为－ A (0< A < qφ 0 ) ．忽略重力．求： (1) 粒子所受静电力的大小； (2) 粒子的运动区间； (3) 粒子的运动周期． 答案 见解析 题型二　电学设计性实验 ④ 节能性原则：应用器材少，耗电少，在限流、分压两种电路都满足实验要求时，由于限流电路结构简单，损耗的电功率小，应优先选用． 2 ． 电路的选择 ① 测量电路的选择 —— “ 好表要内接”：越接近理想表，其分流或分压的影响越小． ② 控制电路的选择 —— “ 以小控大用分压”：因为并联等效电路主要由小电阻决定．必须采用分压式的三种情况：电压从零调；限流时控制不住电流；电压调节范围大． 3 ． 电路设计的常见技巧 (1) 电表的反常规使用 ① 内阻已知的电压表，可以当电流表使用． ② 内阻已知的电流表，可以当电压表使用． (2) 定值电阻的活用 ① 当保护电阻用 ( 满足安全性原则 ) ． ② 减少系统误差，提高精确度 ( 满足精确性原则 ) ． ③ 改装电表，扩大电流表或电压表的量程． ④ 已知通过电流时，可以当电压表使用． ⑤ 已知两端电压时，可以当电流表使用． (3) 滑动变阻器的粗调和微调 ① 限流电路中，对测量电路而言，总电阻较大的变阻器起粗调作用，总电阻较小的变阻器起微调作用． ② 分压电路中，变阻器的粗、微调作用正好与限流电路相反． 【考题 2 】 (1) 某研究小组的同学为了测量某一电阻 R x 的阻值， A 同学先用多用电表进行粗测．使用多用电表欧姆挡时，将选择开关调到欧姆挡“ ×10” 挡位并调零，测量时发现指针向右偏转角度太大，这时他应该：先将选择开关换成欧姆挡的“ __________” 挡位，将红、黑表笔短接，再进行 __________ ，使指针指在欧姆刻度的“ 0” 处；再次测量电阻 R x 的阻值时，指针在刻度盘上停留的位置如图甲所示，则所测量的阻值为 __________ Ω. ×1 　 欧姆调零 　 18 　 甲 (2) 为进一步精确测量该电阻，实验台上摆放有以下器材： A ．电流表 ( 量程 0 ～ 150 mA ，内阻约 2.0 Ω) B ．电流表 ( 量程 0 ～ 0.6 A ，内阻约 0.5 Ω) C ．电阻箱 ( 最大电阻为 99.99 Ω) D ．电阻箱 ( 最大电阻为 999.9 Ω) E ．电源 ( 电动势 3 V ，内阻为 0.8 Ω) F ．单刀单掷开关 2 个 G ．导线若干 B 同学设计的电路图如图乙所示，现按照如下实验步骤完成实验： 乙 ① 调节电阻箱，使电阻箱有合适的阻值 R 1 ，仅闭合 S 1 ，使电流表指针有较大的偏转且读数为 I ； ② 保持开关 S 1 闭合，闭合开关 S 2 ，再次调节电阻箱的阻值为 R 2 ，使电流表的读数仍为 I . a ．根据实验步骤和实验器材规格可知，电流表应选择 __________( 填器材前字母 ) ． b ．根据实验步骤可知，待测电阻 R x ＝ __________( 用题目所给测量数据表示 ) ． A 　 R 2 － R 1 　 丙 2.2 　 解析 (1) 测电阻时用 “ × 10 ” 挡位并调零，测量时指针向右偏转角度太大，说明所选挡位太大，为准确测出电阻，应先将选择开关换成欧姆挡的 “ × 1 ” 挡位，将红、黑表笔短接，再进行欧姆调零；由图示表盘可知，所测量电阻的值为 R x ＝ 18 × 1 Ω ＝ 18 Ω. 1 ． 复合场 一般是指电场、磁场和重力场并存，或其中两种场并存，或分区域存在． ( 速度选择器就是带电粒子在复合场运动规律的应用 ) 2 ． 三种场力的特点 (1) 重力的方向始终竖直向下，重力做功与路径无关，重力做的功等于重力势能的减少量． 题型三　带电粒子在复合场中的运动 (2) 电场力的方向与电场方向相同或相反，电场力做功与路径无关，电场力做的功等于电势能的减少量． (3) 洛伦兹力的大小和速度方向与磁场方向的夹角有关，方向始终垂直于速度 v 和磁感应强度 B 共同决定的平面．无论带电粒子做什么运动，洛伦兹力始终不做功． 3 ． 带电粒子在复合场中的运动规律及解决办法 带电粒子在复合场中运动时，其运动状态是由粒子所受电场力、洛伦兹力和重力的共同作用来决定的，对于有轨道约束的运动，还要考虑弹力、摩擦力对运动的影响，带电粒子在复合场中的运动情况及解题方法如下 (1) 带电粒子在复合场中处于静止或匀速直线运动状态时，带电粒子所受合力为零，应利用平衡条件列方程求解． (2) 带电粒子做匀速圆周运动时，重力和电场力平衡，洛伦兹力提供向心力，应利用平衡方程和向心力公式求解． (3) 当带电粒子在复合场中做非匀变速曲线运动时，带电粒子所受洛伦兹力必不为零，且其大小和方向不断变化，但洛伦兹力不做功，这类问题一般应用动能定理求解． 【考题 3 】 如图甲所示，空间存在一范围足够大的垂直于 xOy 平面向外的匀强磁场，磁感应强度大小为 B . 让质量为 m ，电量为 q ( q >0) 的粒子从坐标原点 O 沿 xOy 平面以大小和方向不同的初速度入射到该磁场中．不计重力和粒子间的影响． (1) 若粒子以初速度 v 1 沿 y 轴正向入射，恰好能经过 x 轴上的 A ( a, 0) 点，求 v 1 的大小； (2) 已知一粒子的初速度大小为 v ( v > v 1 ) ，为使该粒子能经过 A ( a, 0) 点，其入射角 θ ( 粒子初速度与 x 轴正向的夹角 ) 有几个？并求出对应的 sin θ 值； (3) 如图乙所示，若在此空间再加入沿 y 轴正向、大小为 E 的匀强电场，一粒子从 O 点以初速度 v 0 沿 y 轴正向发射．研究表明：粒子在 xOy 平面内做周期性运动，且在任一时刻，粒子速度的 x 分量 v x 与其所在位置的 y 坐标成正比，比例系数与场强大小 E 无关．求该粒子运动过程中的最大速度值 v m . 模块核心素养 素养一　构建物理模型思想 理想化模型是从实际物体或实际情景中抽象出来的，以我们所研究的问题为中心，保留主要条件，忽略次要条件，将实际问题理想化，构建出便于研究的物理模型，这种思想是物理学研究的重要思想，也是顺利解决物理问题的重要思路． 如点电荷就是忽略实际带电体的形状和大小，保留其质量和电荷量而形成的一种理想化模型．带电粒子在匀强电场中运动时，可忽略其重力，构建匀加速直线运动或类平抛运动模型．带电粒子在匀强磁场中运动时，不考虑重力，构建匀速圆周运动模型等． 2 ． 导体切割磁感线模型 【典例 2 】 电磁流量计广泛用于测量可导电流体 ( 如污水 ) 在管中的流量 ( 单位时间内通过管内某横截面的流体的体积 ) ．为了简化，假设流量计是如图所示的横截面为矩形的一段管道，其中空的部分的长、宽、高分别为图中的 a 、 b 、 c . 流量计的两端与输送流体的管道相连 ( 图中虚线 ) ，图中流量计的上、下两面是金属材料，前、后两面是绝缘材料，现给流量计所在处加磁感应强度为 B 的匀强磁场，磁场方向垂直于前、后两面， 解析 如图甲所示，两极板 ( 上、下两面 ) 间距为 c ，磁场方向如图中箭头所示．当外电路断开时，运动电荷受洛伦兹力作用而偏转，两极板带电 ( 两极板作为电路供电部分 ) 而使电荷受电场力，当运动电荷稳定时，两极板所带电荷量最多，两极板间的电压最大，等于电源电动势 E . 测量电路可等效成如图乙所示． 素养二　物理补偿思维方法 物理补偿思维方法是对一些散乱的，有残缺的物体或物理图景归纳整理，使其规律得以显现的很好的方法．使用时常见模式是这样的：对于残缺的问题 A ，先给其补充上条件 B ( 易于解决 ) ，从而建立起另一个较圆满的易解决的 C ，于是求解 A 的问题就演化成求解两个易解决的 B 和 C 的问题．所以补偿思维方法是一种技巧性很强的方法． 素养三　对称性思维方法 物理学中的对称性是指物理规律在某些变换中 ( 主要是指时间和空间 ) 具有不变性，大家所熟知的带电粒子在电、磁场中运动时出现的非常优美、非常规则的几何图案，就是这种不变性的具体体现．然而对称性远不止这些，自然界普遍存在着优美和谐的对称美，需要我们透过现象世界和表层迷雾去发现． 【典例 5 】 如图所示匀强电场 E 的区域内，在 O 点处放置一点电荷＋ Q ， a 、 b 、 c 、 d 、 e 、 f 为以 O 点为球心的球面上的点， aecf 平面与电场线平行， bedf 平面与电场线垂直，则下列说法正确的是 ( 　　 ) A ． b 、 d 两点的电场强度相同 B ． a 点的电势等于 f 点的电势 C ．点电荷＋ q 在球面上任意两点之间移动时，电场力一定不做功 D ．将点电荷＋ q 在球面上任意两点之间移动，从球面上 a 点移动到 c 点的电势能变化量最大 答案 D 解析 点电荷＋ Q 在 b 点产生的电场方向为竖直向上，在 d 点产生的电场方向为竖直向下，匀强电场方向水平向右，根据平行四边形定则可知， b 点的合场强斜向右上方， d 点的合场强斜向右下方，两点场强大小相同，方向不同，电场强度不同，选项 A 错误；将一个试探正电荷由 a 点移动到 f 点，点电荷电场力不做功，匀强电场的电场力做正功，故合力做正功，电势能减小，电势降低，选项 B 错误； 当电荷＋ q 沿着球面上的 bedf 移动时，匀强电场的电场力不做功，点电荷电场力也不做功，故合电场力不做功，选项 C 错误；将点电荷＋ q 在球面上任意两点之间移动，点电荷电场力不做功，从 a 点移动到 c 点，匀强电场的电场力做功最大，故合力做功最大，选项 D 正确． 素养四　等效思维方法 等效思维方法是在效果相同的前提下对研究过程、条件、对象进行等效替代的方法，替代的目的是使问题简化，求解方便，它的应用十分广泛，在电学中有等效电场，等效电源，等效电阻 …… 关键是替代中一定要“等效”． 1 ． 等效电源 【典例 6 】 如图所示，虚线框内各元件的参数均不知．在 a 、 b 端接一只 R 1 ＝ 10 Ω 的电阻时，测得其电流 I 1 ＝ 1 A ；若在 a 、 b 间换接电阻 R 2 ＝ 18 Ω 时，测得其电流 I 2 ＝ 0.6 A ；换接电阻 R 3 时，测得其电流 I 3 ＝ 0.1 A ，则 R 3 的阻值为多少？ 解析 视虚线框内整体为一电源，且电动势为 E ，内阻为 r ，则 E ＝ I 1 ( R 1 ＋ r ) ， E ＝ I 2 ( R 2 ＋ r ) ， E ＝ I 3 ( R 3 ＋ r ) ， 解得 E ＝ 12 V ， r ＝ 2 Ω ， R 3 ＝ 118 Ω. 答案 118 Ω 2 ． 等效加速度 【典例 7 】 如图所示，绝缘粗糙的竖直平面 MN 左侧同时存在相互垂直的匀强电场和匀强磁场，电场方向水平向右，电场强度大小为 E ，磁场方向垂直纸面向外，磁感应强度大小为 B . 一质量为 m 、电荷量为 q 的带正电的小滑块从 A 点由静止开始沿 MN 下滑，到达 C 点时离开 MN 做曲线运动． A 、 C 两点间距离为 h ，重力加速度为 g . (1) 求小滑块运动到 C 点时的速度大小 v C ； (2) 求小滑块从 A 点运动到 C 点过程中克服摩擦力做的功 W f ； (3) 若 D 点为小滑块在电场力、洛伦兹力及重力作用下运动过程中速度最大的位置，当小滑块运动到 D 点时撤去磁场，此后小滑块继续运动到水平地面上的 P 点．已知小滑块在 D 点时的速度大小为 v D ，从 D 点运动到 P 点的时间为 t ，求小滑块运动到 P 点时速度的大小 v P . 素养五　数形结合思想 数形结合是一种重要的数学方法，其应用大致可分为两种情况：借助于数的精确性来阐明形的某些属性，或借助于形的几何直观性来阐明数之间某种关系．在物理学中，两个物理量间的函数关系，不仅可以用公式表示，还可以用图象表示．物理图象是数与形相结合的产物，是具体与抽象相结合的体现，它能直观、形象、简洁的展现两个物理之间的关系，清晰的表达物理过程，正确地反映实验规律． 甲 乙 (1) 出射粒子的动能 E k ； (2) 粒子从飘入狭缝至动能达到 E k 所需的总时间 t 0 ； (3) 要使飘入狭缝的粒子中有超过 99% 能射出， d 应满足的条件． 素养六　极限思维方法 极限思维方法是将问题推向极端状态的过程中，着眼一些物理量在连续变化过程中的变化趋势及一般规律在极限值下的表现或者说极限值下一般规律的表现，从而对问题进行分析和推理的一种思维办法． 【典例 9 】 如图所示，一束电子以大小不同的速率沿图示方向飞入横截面为一正方形的匀强磁场区，在从 ab 边离开磁场的电子中，下列判断正确的是 ( 　　 ) A ．从 b 点离开的电子速度最小 B ．从 b 点离开的电子在磁场中运动时间最长 C ．从 b 点离开的电子速度偏转角最大 D ．在磁场中运动时间相同的电子，其轨迹一定重合 D 由图可知，粒子从 b 点离开时，偏转角最小，从 a 点离开时，偏转角最大，从 b 点离开速度的偏转角最小，故时间最短，选项 B 、 C 错误；因电子运动周期相同，若电子在磁场中的运动时间相同，则说明电子的偏转角相同，故电子的轨迹一定相同，选项 D 正确．