【物理】2019届一轮复习人教版　探究弹力和弹簧伸长的关系学案 9页

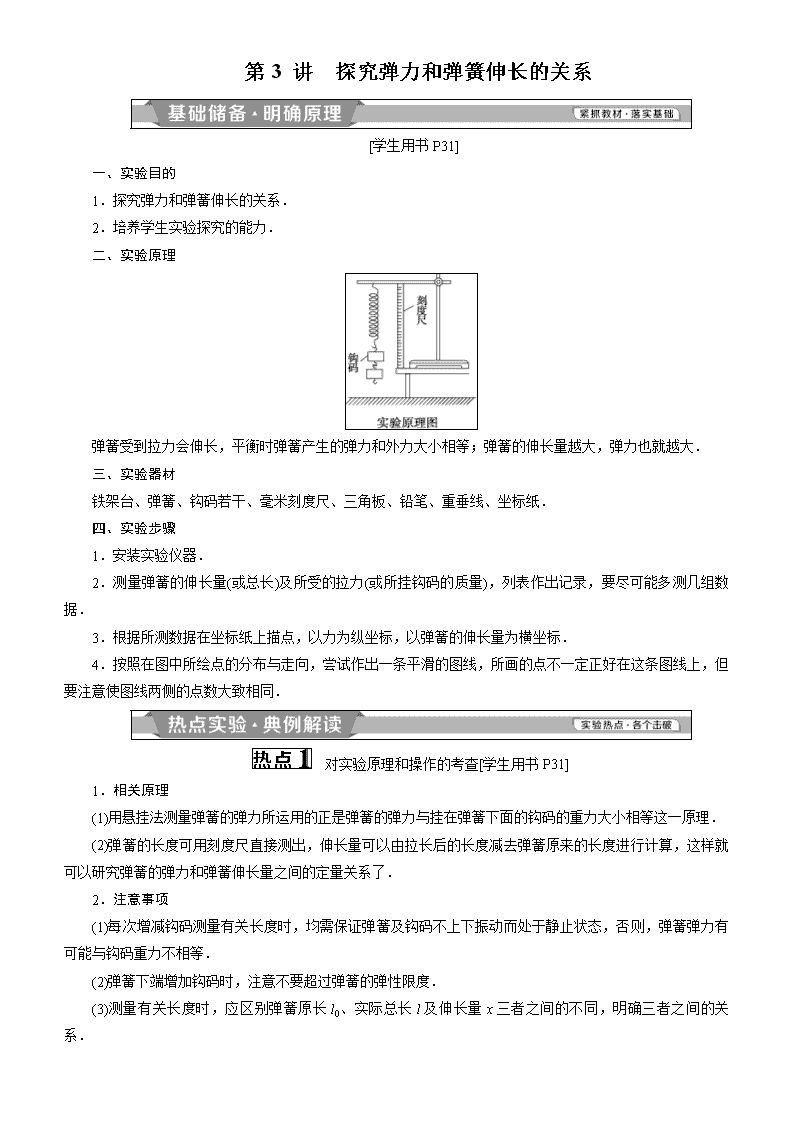
第3 讲　探究弹力和弹簧伸长的关系 ‎ [学生用书P31]‎ 一、实验目的 ‎1．探究弹力和弹簧伸长的关系．‎ ‎2．培养学生实验探究的能力．‎ 二、实验原理 弹簧受到拉力会伸长，平衡时弹簧产生的弹力和外力大小相等；弹簧的伸长量越大，弹力也就越大．‎ 三、实验器材 铁架台、弹簧、钩码若干、毫米刻度尺、三角板、铅笔、重垂线、坐标纸．‎ 四、实验步骤 ‎1．安装实验仪器．‎ ‎2．测量弹簧的伸长量(或总长)及所受的拉力(或所挂钩码的质量)，列表作出记录，要尽可能多测几组数据．‎ ‎3．根据所测数据在坐标纸上描点，以力为纵坐标，以弹簧的伸长量为横坐标．‎ ‎4．按照在图中所绘点的分布与走向，尝试作出一条平滑的图线，所画的点不一定正好在这条图线上，但要注意使图线两侧的点数大致相同．‎ ‎　对实验原理和操作的考查[学生用书P31]‎ ‎1．相关原理 ‎(1)用悬挂法测量弹簧的弹力所运用的正是弹簧的弹力与挂在弹簧下面的钩码的重力大小相等这一原理．‎ ‎(2)弹簧的长度可用刻度尺直接测出，伸长量可以由拉长后的长度减去弹簧原来的长度进行计算，这样就可以研究弹簧的弹力和弹簧伸长量之间的定量关系了．‎ ‎2．注意事项 ‎(1)每次增减钩码测量有关长度时，均需保证弹簧及钩码不上下振动而处于静止状态，否则，弹簧弹力有可能与钩码重力不相等．‎ ‎(2)弹簧下端增加钩码时，注意不要超过弹簧的弹性限度．‎ ‎(3)测量有关长度时，应区别弹簧原长l0、实际总长l及伸长量x三者之间的不同，明确三者之间的关系．‎ ‎(4)建立平面直角坐标系时，两轴上单位长度所代表的量值要适当，不可过大，也不可过小．‎ ‎(5)描线的原则是，尽量使各点落在描画出的线上，少数点分布于线两侧，描出的线不应是折线，而应是平滑的曲线．‎ ‎【典题例析】‎ ‎　(2018·广东茂名信宜中学月考) 如图甲所示，用铁架台、弹簧和多个已知质量且质量相等的钩码探究在弹性限度内弹簧弹力与弹簧伸长量的关系．‎ ‎　‎ ‎(1)为完成实验，还需要的实验器材有_______________________________________________．‎ ‎(2)实验中需要测量的物理量有____________________________________________________________‎ ‎___________________________________________.‎ ‎(3)图乙是弹簧弹力F与弹簧伸长量x的F－x图线，由此可求出弹簧的劲度系数为________N/m.图线不过原点的原因是由于________________________________________________________________________．‎ ‎(4)为完成该实验，设计的实验步骤如下：‎ A．以弹簧伸长量为横坐标，以弹力为纵坐标，描出各组(x，F)对应的点，并用平滑的曲线连接起来；‎ B．记下弹簧不挂钩码时其下端的刻度尺上的刻度l0；‎ C．将铁架台固定于桌子上，并将弹簧的一端系于横梁上，在弹簧附近竖直固定一把刻度尺；‎ D．依次在弹簧下端挂上1个、2个、3个、4个…钩码，并分别记下钩码静止时弹簧下端所对应的刻度，并记录在表格内，然后取下钩码；‎ E．以弹簧伸长量为自变量，写出弹力与伸长量的关系式．首先尝试写成一次函数，如果不行，则考虑二次函数；‎ F．解释函数表达式中常数的物理意义；‎ G．整理仪器．‎ 请将以上步骤按操作的先后顺序排列出来：________________________________________________________________________.‎ ‎[解析]　(1)实验需要测弹簧的长度、形变量，故还需要的实验器材有：刻度尺．‎ ‎(2)为了测量弹簧的形变量，实验中还应测量弹簧原长、弹簧所受外力与对应的伸长量(或与对应的长度)．‎ ‎(3)图线的斜率表示弹簧的劲度系数，则k＝ N/m＝200 N/m；图线不过原点说明没有力时有了形变量，故说明弹簧有自身的重力存在．‎ ‎(4)实验中要先组装器材，即CB，再进行实验，即D，然后数据处理，分析解释表达式，最后整理仪器，即AEFG.所以先后顺序为CBDAEFG.‎ ‎[答案]　(1)刻度尺　(2)弹簧原长、弹簧所受外力与对应的伸长量(或与对应的长度)　(3)200　弹簧自身重力 ‎(4)CBDAEFG ‎　1.(1)在“探究弹力和弹簧伸长的关系”的实验中，以下说法正确的是________．‎ A．弹簧被拉伸时，不能超出它的弹性限度 B．用悬挂钩码的方法给弹簧施加拉力，应保证弹簧位于竖直位置且处于平衡状态 C．用直尺测得弹簧的长度即为弹簧的伸长量 D．用几根不同的弹簧，分别测出几组拉力与伸长量，得出拉力与伸长量之比相等 ‎(2)某同学做“探究弹力和弹簧伸长的关系”的实验，他先把弹簧平放在桌面上使其自然伸长，用直尺测出弹簧的原长L0，再把弹簧竖直悬挂起来，挂上钩码后测出弹簧伸长后的长度L，把L－L0作为弹簧的伸长量x，这样操作，由于弹簧自身重力的影响，最后画出的图线可能是________．‎ 解析：(2)由于弹簧自身重力的影响，未挂钩码时，弹簧就伸长了一定长度，故只有C正确．‎ 答案：(1)AB　(2)C ‎　对实验数据处理和误差分析的考查[学生用书P32]‎ ‎1．数据处理 ‎(1)解析法：以弹簧的伸长量为自变量，写出图线所代表的函数解析式，首先尝试一次函数，如果不行再考虑二次函数．‎ ‎(2)列表法：将测得的F、x填入设计好的表格中，可以发现弹力F与弹簧伸长量x的比值在误差允许范围内是相等的．‎ ‎(3)图象法：以弹簧伸长量x为横坐标，弹力F为纵坐标，描出F、x各组数据相应的点，作出的拟合曲线是一条过坐标原点的直线．‎ ‎2．误差分析 ‎(1)钩码标值不准确、弹簧长度测量不准确带来误差．‎ ‎(2)画图时描点及连线不准确也会带来误差．‎ ‎【典题例析】‎ ‎　(2018·安徽淮北一中月考)在“探究弹力和弹簧伸长量的关系，并测量弹簧的劲度系数”的实验中，实验装置如图1所示，所用的每个钩码的重力相当于对弹簧提供了向右恒定的拉力，实验时先测出不挂钩码时弹簧的自然长度，再将5个钩码逐个挂在绳子的下端，每次测量相应的弹簧的总长度．‎ ‎(1)某同学通过以上实验测量后把6组实验数据描点在坐标系图2中，请作出F－L图线．‎ ‎(2)由此图线可得出弹簧的原长L0＝________cm，劲度系数k＝________N/m.‎ ‎(3)试根据该同学以上的实验情况，帮助他设计一个记录实验数据的表格(不必填写其实验测得的具体数据)．‎ ‎(4)该同学实验时，把弹簧水平放置与弹簧悬挂放置相比较 优点在于：__________________________________________________；‎ 缺点在于：______________________________________________________.‎ ‎[解析]　(1)F－L图线如图所示．‎ ‎(2)图象的横截距表示弹力为零时的弹簧的长度，此时弹簧的长度为原长，所以弹簧的原长L0＝5 cm，图象的斜率表示弹簧的劲度系数，故有k＝＝ N/m＝20 N/m.‎ ‎(3)试根据该同学以上的实验情况，记录实验数据的表格为：‎ 钩码个数 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 弹力F/N 弹簧长度 L/(×10－2 m)‎ ‎(4)优点在于：可以避免弹簧自身重力对实验的影响，缺点在于：弹簧与桌面及绳子与滑轮间存在的摩擦会造成实验误差．‎ ‎[答案]　(1)如解析图所示　(2)5　20　(3)见解析　‎ ‎(4)可以避免弹簧自身重力对实验的影响　弹簧与桌面及绳子与滑轮间存在的摩擦会造成实验误差 ‎　2.为了探究弹簧弹力F和弹簧伸长量x的关系，李强同学选了甲、乙两根规格不同的弹簧进行测试，根据测得的数据绘出如图所示的图象，‎ ‎(1)从图象上看，该同学没能完全按实验要求做，使图象上端成为曲线，图象上端成为曲线是因为______________________________．‎ ‎(2)这两根弹簧的劲度系数分别为：甲弹簧为______ N/m，乙弹簧为________ N/m.若要制作一个精确度相对较高的弹簧测力计，应选弹簧________(选填“甲”或“乙”)．‎ 解析：(1)在弹性范围内弹簧的弹力与形变量成正比，超过弹簧的弹性范围，则此规律不成立，所以所给的图象上端成为曲线，是因为形变量超过弹簧的弹性限度．‎ ‎(2)甲、乙两根弹簧的劲度系数分别为：‎ k甲＝＝ N/m＝66.7 N/m k乙＝＝ N/m＝200 N/m 要制作一个精确程度较高的弹簧测力计，应选用一定的外力作用时形变量大的弹簧，故选甲弹簧．‎ 答案：(1)形变量超过弹簧的弹性限度 ‎(2)66.7　200　甲 ‎　创新实验[学生用书P32]‎ ‎　本实验的系统误差来自弹簧的重力，所以改进实验的思路应该是尽可能减小弹簧自身重力的影响．‎ 对本实验的创新迁移可能从以下角度进行：‎ ‎1．一个方案是将弹簧穿过一根水平光滑的杆，在水平方向做实验；或是选择劲度系数较小的轻弹簧，通过减小读数的相对误差来提高实验的精确度．‎ ‎2．利用计算机及传感器技术，将弹簧水平放置，且一端固定在传感器上，传感器与计算机相连，对弹簧施加变化的作用力(拉力或推力)时，计算机上得到弹簧弹力和弹簧形变量的关系图象(如图甲、乙所示)，分析图象得出结论．‎ ‎3．运用k＝来处理数据 ‎(1)将“弹力变化量”转化为“质量变化量”；‎ ‎(2)将“弹簧伸长量”转化为“弹簧长度变化量”．‎ ‎【典题例析】‎ ‎　(2018·云南昆明模拟)在探究弹簧的弹力与伸长量之间关系的实验中，所用装置如图甲所示，将轻弹簧的一端固定，另一端与力传感器连接，其伸长量通过刻度尺测得，某同学的实验数据列于下表中：‎ 伸长量x/(×10－2 m)‎ ‎2.00‎ ‎4.00‎ ‎6.00‎ ‎8.00‎ ‎10.00‎ 弹力F/N ‎1.50‎ ‎2.93‎ ‎4.55‎ ‎5.98‎ ‎7.50‎ ‎(1)以x为横坐标、F为纵坐标，在图乙的坐标纸上描绘出能正确反映这一弹簧的弹力与伸长量之间关系的图线．‎ ‎(2)由图线求得这一弹簧的劲度系数为________．(保留三位有效数字)‎ ‎[解析] (1)描点作图，如图．‎ ‎(2)根据解析(1)中图象，该直线为过原点的一条倾斜直线，即弹力与伸长量成正比，图象的斜率表示弹簧的劲度系数，k＝＝75.0 N/m.　‎ ‎[答案] (1)见解析图　(2)75.0 N/m ‎　3.(2018·上饶高三模拟)在探究弹力和弹簧伸长的关系时，某同学先按图(a)对弹簧甲进行探究，然后把弹簧甲和弹簧乙并联起来按图(b)进行探究．在弹性限度内，将质量为m＝50 g的钩码逐个挂在弹簧下端，分别测得图(a)、图(b)中弹簧的长度L1、L2如表所示．‎ 钩码个数 ‎1‎ ‎2‎ ‎3‎ ‎4‎ L1/cm ‎30.00‎ ‎31.04‎ ‎32.02‎ ‎33.02‎ L2/cm ‎29.33‎ ‎29.65‎ ‎29.97‎ ‎30.30‎ 已知重力加速度g＝10 m/s2，计算弹簧甲的劲度系数k＝________N/m，由表中数据________(填“能”或“不能”)计算出弹簧乙的劲度系数．‎ 解析：分析图(a)中，钩码数量和弹簧伸长量的关系为每增加一个钩码，弹簧长度伸长约1 cm，所以弹簧劲度系数k1＝＝＝＝50 N/m.分析图(b)中可得，每增加一个钩码，弹簧伸长约0.3 cm，即k1×0.003＋k2×0.003＝mg，根据弹簧甲的劲度系数可以求出弹簧乙的劲度系数．‎ 答案：50　能 ‎　[学生用书P33]‎ ‎1．(2015·高考四川卷)某同学在“探究弹力和弹簧伸长的关系”时，安装好实验装置，让刻度尺零刻度与弹簧上端平齐，在弹簧下端挂1个钩码，静止时弹簧长度为l1，如图甲所示，图乙是此时固定在弹簧挂钩上的指针在刻度尺(最小分度是1毫米)上位置的放大图，示数l1＝________cm.在弹簧下端分别挂2个、3个、4个、5个相同钩码，静止时弹簧长度分别是l2、l3、l4、l5.已知每个钩码质量是50 g，挂2个钩码时，弹簧弹力F2＝________N(当地重力加速度g＝9.8 m/s2)．要得到弹簧伸长量x，还需要测量的是________．作出F－x曲线，得到弹力与弹簧伸长量的关系．‎ ‎　　　　　　　甲　　　　　　　乙 解析：由题图乙知l1＝25.85 cm.挂两个钩码时，弹簧弹力F2＝0.98 N．要测弹簧伸长量，还需要测量弹簧的原长．‎ 答案：25.85　0.98　弹簧原长 ‎2．(2018·深圳高三模拟)某同学利用如图甲装置做“探究弹簧弹力大小与其长度的关系”的实验．‎ ‎(1)在安装刻度尺时，必须使刻度尺保持________状态．‎ ‎(2)他通过实验得到如图乙所示的弹力大小F与弹簧长度x的关系图象．由此图象可得该弹簧的原长x0＝________cm，劲度系数k＝________N/m.‎ ‎(3)他又利用本实验原理把该弹簧做成一把弹簧测力计，当弹簧测力计上的示数如图丙所示时，该弹簧的长度x＝________cm.‎ 解析：(2)x0为乙图中F＝0时的x值，即x0＝4 cm.‎ k＝＝ N/m＝50 N/m.‎ ‎(3)测力计示数F＝3.0 N，由乙图知弹簧长度x＝10 cm.‎ 答案：(1)竖直　(2)4　50　(3)10‎ ‎3．(高考全国卷Ⅱ)某实验小组探究弹簧的劲度系数k与其长度(圈数)的关系．实验装置如图(a)所示：一均匀长弹簧竖直悬挂，7个指针P0、P1、P2、P3、P4、P5、P6分别固定在弹簧上距悬点0、10、20、30、40、50、60圈处；通过旁边竖直放置的刻度尺，可以读出指针的位置，P0指向0刻度．设弹簧下端未挂重物时，各指针的位置记为x0；挂有质量为0.100 kg的砝码时，各指针的位置记为x.测量结果及部分计算结果如下表所示(n为弹簧的圈数，取重力加速度为9.80 m/s2)．已知实验所用弹簧总圈数为60，整个弹簧的自由长度为11.88 cm.‎ P1‎ P2‎ P3‎ P4‎ P5‎ P6‎ x0(cm)‎ ‎2.04‎ ‎4.06‎ ‎6.06‎ ‎8.05‎ ‎10.03‎ ‎12.01‎ x(cm)‎ ‎2.64‎ ‎5.26‎ ‎7.81‎ ‎10.30‎ ‎12.93‎ ‎15.41‎ n ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎60‎ k(N/m)‎ ‎163‎ ‎①‎ ‎56.0‎ ‎43.6‎ ‎33.8‎ ‎28.8‎ (m/N)‎ ‎0.006 1‎ ‎②‎ ‎0.017 9‎ ‎0.022 9‎ ‎0.029 6‎ ‎0.034 7‎ ‎(1)将表中数据补充完整：①________，②________．‎ ‎(2)以n为横坐标，为纵坐标，在图(b)给出的坐标纸上画出－n图象．‎ ‎(3)图(b)中画出的直线可近似认为通过原点．若从实验中所用的弹簧截取圈数为n的一段弹簧，该弹簧的劲度系数k与其圈数n的关系的表达式为k＝________N/m；该弹簧的劲度系数k与其自由长度l0(单位为m)的关系的表达式为k＝________N/m.‎ 解析：(1)①k＝＝≈81.7 N/m.‎ ‎②＝ m/N≈0.012 2 m/N.‎ ‎(2)描点法，画一条直线，让大部分的点都落在直线上，或均匀分布在直线两侧．‎ ‎(3)设直线的斜率为a，则有＝an，即k＝·，通过计算斜率即可求得；弹簧共60圈，则有n＝，把其代入k＝·中可求得．‎ 答案：(1)①81.7　②0.012 2　(2)如图所示 ‎(3) ‎4．(高考浙江卷)在“探究弹力和弹簧伸长的关系”时，某同学把两根弹簧如图甲连接起来进行探究．‎ ‎(1)某次测量如图乙所示，指针示数为________cm.‎ ‎(2)在弹性限度内，将50 g的钩码逐个挂在弹簧下端，得到指针A、B的示数LA和LB如下表所示．用表中数据计算弹簧Ⅰ的劲度系数为________ N/m(重力加速度g＝10 m/s2)．由表中数据________(填“能”或“不能”)计算出弹簧Ⅱ的劲度系数．‎ 钩码数 ‎1‎ ‎2‎ ‎3‎ ‎4‎ LA/cm ‎15.71‎ ‎19.71‎ ‎23.66‎ ‎27.76‎ LB/cm ‎29.96‎ ‎35.76‎ ‎41.51‎ ‎47.36‎ 解析：(1)刻度尺读数需要估读到精确度的下一位，从题图乙可知指针示数为16.00 cm，考虑到误差范围，15.95～16.05 cm均算对．‎ ‎(2)由胡克定律F＝kΔx，结合表格数据可知弹簧Ⅰ的劲度系数k1＝ N/m＝12.5 N/m，考虑误差范围情况下12.2～12.8 N/m均算正确；对于计算弹簧Ⅱ的劲度系数，只需要测出弹簧Ⅱ的形变量，结合两个指针的读数，可知指针B的示数变化量减去指针A的示数变化量，就是弹簧Ⅱ的形变量，所以能求出弹簧Ⅱ的劲度系数．‎ 答案：(1)16.00(有效数字位数正确，15.95～16.05均可)‎ ‎(2)12.5(12.2～12.8均可)　能