【物理】2019届一轮复习人教版　机械能守恒定律　能量守恒定律学案 17页

第9讲　机械能守恒定律　能量守恒定律 考试内容及要求 知识内容 学考要求 ‎2015.10考题 ‎2016.4考题 ‎2016.10考题 ‎2017.4考题 ‎2017.11考题 ‎2018.4考题 ‎2018.6考题 机械能守恒定律 d ‎8‎ ‎20‎ ‎12‎ ‎9‎ ‎10‎ 能量守恒定律与 能源 c ‎5‎ ‎4、20‎ 一、机械能守恒定律 ‎1．机械能 ‎(1)机械能：动能和势能的总和称为机械能，其中势能包括重力势能和弹性势能．‎ ‎(2)表达式：E＝Ek＋Ep.‎ ‎2．机械能守恒定律 ‎(1)内容：在只有重力或弹力做功的物体系统内，动能和势能可以互相转化，而总的机械能保持不变．‎ ‎(2)表达式：‎ ‎①mv12＋mgh1＝mv22＋mgh2；‎ ‎②Ek1＋Ep1＝Ek2＋Ep2.‎ ‎3．机械能守恒的条件 只有重力(或弹力)做功；只发生动能和势能的转化．‎ ‎4．机械能守恒的判断 ‎(1)利用机械能的定义判断：分析动能和势能的和是否变化．‎ ‎(2)用做功判断：若物体系统内只有重力(或弹力)做功，或有其他力做功，但其他力做功的代数和为零，则机械能守恒．‎ ‎(3)用能量转化来判断：若物体系统内只有动能和势能的相互转化而无机械能与其他形式的能的转化，则物体系统机械能守恒．‎ 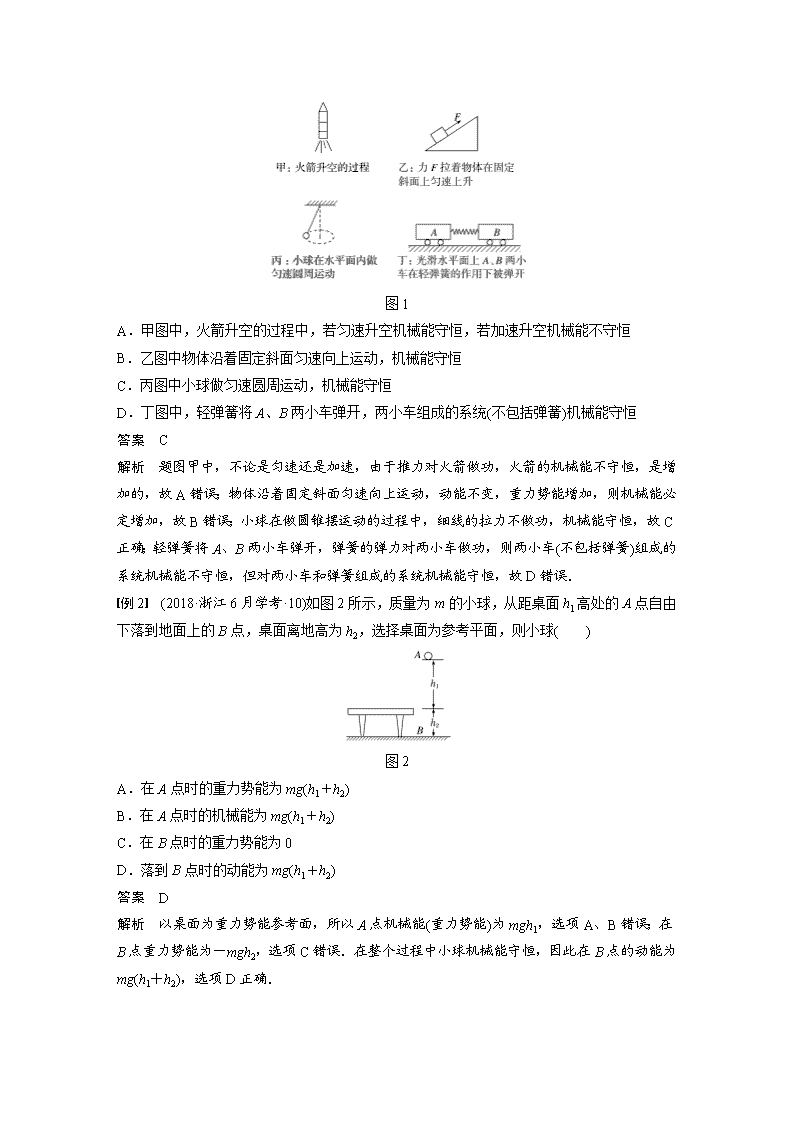例1　(2018·嘉兴市第一中学期中测试)如图1所示，根据机械能守恒条件，下列说法正确的是(　　)‎ 图1‎ A．甲图中，火箭升空的过程中，若匀速升空机械能守恒，若加速升空机械能不守恒 B．乙图中物体沿着固定斜面匀速向上运动，机械能守恒 C．丙图中小球做匀速圆周运动，机械能守恒 D．丁图中，轻弹簧将A、B两小车弹开，两小车组成的系统(不包括弹簧)机械能守恒 答案　C 解析　题图甲中，不论是匀速还是加速，由于推力对火箭做功，火箭的机械能不守恒，是增加的，故A错误；物体沿着固定斜面匀速向上运动，动能不变，重力势能增加，则机械能必定增加，故B错误；小球在做圆锥摆运动的过程中，细线的拉力不做功，机械能守恒，故C正确；轻弹簧将A、B两小车弹开，弹簧的弹力对两小车做功，则两小车(不包括弹簧)组成的系统机械能不守恒，但对两小车和弹簧组成的系统机械能守恒，故D错误．‎ 例2　(2018·浙江6月学考·10)如图2所示，质量为m的小球，从距桌面h1高处的A点自由下落到地面上的B点，桌面离地高为h2，选择桌面为参考平面，则小球(　　)‎ 图2‎ A．在A点时的重力势能为mg(h1＋h2)‎ B．在A点时的机械能为mg(h1＋h2)‎ C．在B点时的重力势能为0‎ D．落到B点时的动能为mg(h1＋h2)‎ 答案　D 解析　以桌面为重力势能参考面，所以A点机械能(重力势能)为mgh1，选项A、B错误；在B点重力势能为－mgh2，选项C错误．在整个过程中小球机械能守恒，因此在B点的动能为mg(h1＋h2)，选项D正确．‎ 二、机械能守恒定律的应用 ‎1．在满足机械能守恒的条件下，无论物体做直线运动还是曲线运动，所受外力是恒力还是变力，均可列出相应的关系式，为解决曲线运动、变力问题提供了简捷、有效的方法．‎ ‎2．当有弹力做功时，弹性势能与动能、重力势能相互间发生转化．需要注意，涉及弹性势能的转化时研究对象是否包括弹簧．‎ ‎3．解决竖直面内圆周运动问题的注意点 ‎(1)竖直面内圆周运动一般为变速圆周运动．‎ ‎(2)确定物体的运动属于“绳模型”还是“杆模型”，充分利用其“约束”或“临界”条件．‎ ‎(3)一般只在最高点或最低点列出动力学方程．‎ ‎(4)运动过程中优先考虑机械能守恒定律或动能定理．‎ 例3　(2018·余姚市第二学期期中)如图3所示，弯曲斜面与半径为R的竖直半圆组成光滑轨道，一个质量为m的小球从高度为4R的A点由静止释放，经过半圆的最高点D后做平抛运动落在水平面的E点，忽略空气阻力(重力加速度为g)，求：‎ 图3‎ ‎(1)小球在D点时的速度大小vD；‎ ‎(2)小球落地点E离半圆轨道最低点B的位移大小x；‎ ‎(3)小球经过半圆轨道的C点(C点与圆心O在同一水平面)时对轨道的压力大小．‎ 答案　见解析 解析　(1)从A点到D点的过程中，由机械能守恒定律：‎ mg·4R＝mg·2R＋mvD2‎ 解得vD＝2 ‎(2)平抛运动过程中：2R＝gt2‎ x＝vDt 解得x＝4R ‎(3)从A点至C点的过程中，由机械能守恒定律：‎ mg·4R＝mgR＋mvC2‎ 解得FN＝m＝6mg 由牛顿第三定律得：FN′＝FN＝6mg.‎ 例4　如图4所示是跳台滑雪的示意图，雪道由倾斜的助滑雪道AB、水平平台BC、着陆雪道CD及减速区DE组成，各雪道间均平滑连接．A处与水平平台间的高度差h＝45 m，CD的倾角为30°.运动员自A处由静止滑下，不计其在雪道ABC滑行和空中飞行时所受的阻力，运动员可视为质点，g取10 m/s2.‎ 图4‎ ‎(1)求运动员滑离平台BC时的速度大小；‎ ‎(2)为保证运动员落在着陆雪道CD上，雪道CD的长度至少为多少？‎ ‎(3)若实际的着陆雪道CD长为150 m，运动员着陆后滑到D点时具有的动能是着陆瞬间动能的80%.在减速区DE滑行s＝100 m后停下，求运动员在减速区所受平均阻力是其重力的多少倍？‎ 答案　(1)30 m/s　(2)120 m　(3)0.84‎ 解析　(1)A到C过程中机械能守恒mgh＝mv 得vC＝＝30 m/s.‎ ‎(2)设落点D′距C的距离为L，由平拋运动规律得：Lcos 30°＝vCt Lsin 30°＝gt2‎ 解得L＝120 m，因此雪道CD的长度至少为120 m.‎ ‎(3)运动员由A运动到落点D′过程中，由机械能守恒定律得：mg(h＋Lsin 30°)＝mvD′2‎ 设运动员在减速区减速过程中所受平均阻力是重力的k倍，‎ 根据动能定理有－kmgs＝0－mvD2‎ 根据题意有mvD2＝0.80×mvD′2‎ 解得k＝0.84.‎ 三、能量守恒定律 ‎1．内容：能量既不会凭空产生，也不会凭空消失，它只能从一种形式转化为另一种形式，或者从一个物体转移到别的物体，在转化或转移的过程中，能量的总量保持不变．‎ ‎2．意义：确认了永动机的不可能性和发现了各种自然现象之间的相互联系与转化．‎ ‎3．节约能源的含义：能量耗散表明，在能源的利用(即能量的转化)过程中，能量在数值上虽未减少，但在可利用的品质上降低了，从便于利用变成了不便于利用．‎ 例5　(2016·浙江4月学考·12)如图5所示的路灯为太阳能路灯，每只路灯的光伏电池板有效采光面积约为0.3 m2.晴天时电池板上每平方米每小时接收到的太阳辐射能约为3×‎ ‎106 J．如果每天等效日照时间约为6 h，光电池一天产生的电能可供30 W的路灯工作8 h．光电池的光电转换效率约为(　　)‎ 图5‎ A．4.8% B．9.6%‎ C．16% D．44%‎ 答案　C 解析　光电池的光电转换效率是转化得到的电能与接收到的光能的比值，即：η＝×100%＝×100%＝16%，故选C.‎ 例6　(2017·浙江名校协作体联考)一弹珠弹射玩具模型如图6所示，水平粗糙管AB内装有一轻弹簧，左端固定，竖直放置的管道BCD光滑，其中CD为半径为R＝0.1 m的圆周，C到地面的地面高度也为R.用质量m1＝0.3 kg的弹珠(可看成质点)将弹簧缓慢压缩到某一确定位置M，弹珠与弹簧不固连，由静止释放后弹珠恰停止在D点，用同种材料、质量为m2＝0.1 kg的弹珠仍将弹簧缓慢压缩到M点释放，由静止释放后弹珠由D点飞出后落在与D点正下方D′点相距x＝0.8 m处，取g＝10 m/s2，不计空气阻力，求：‎ 图6‎ ‎(1)质量为m2的弹珠从D点飞出时的速度大小；‎ ‎(2)质量为m2的弹珠在D点时对轨道的弹力；‎ ‎(3)弹簧被缓慢压缩到M点时储存的弹性势能．‎ 答案　(1)4 m/s　(2)15 N，方向竖直向上　(3)1.2 J 解析　(1)质量为m2的弹珠从D点飞出后做平抛运动，‎ 由平抛运动规律得 ‎2R＝gt2，x＝vDt 代入数据得vD＝4 m/s.‎ ‎(2)质量为m2的弹珠经D点时，由牛顿第二定律得 m2g＋FN＝m2 则FN＝m2－m2g＝15 N，方向竖直向下 由牛顿第三定律知质量为m2的弹珠在D点时对轨道的弹力FN′＝FN＝15 N，方向竖直向上．‎ ‎(3)对质量为m1的弹珠，从静止释放到D的过程中，由能量守恒定律得 Ep＝μm1gxMB＋m1g·2R 对质量为m2的弹珠，则有 Ep＝μm2gxMB＋m2g·2R＋m2vD2‎ 代入数据可得Ep＝1.2 J.‎ 四、功能关系 功是能量转化的量度，某种力做功往往与某种形式的能量转化相对应，具体功能关系如下：‎ 功 能的变化 表达式 重力做功 重力势能变化 WG＝Ep1－Ep2‎ 弹力做功 弹性势能变化 W弹＝Ep1－Ep2‎ 合力做功 动能变化 W合＝Ek2－Ek1‎ 除重力(或系 统内弹力)外 其他力做功 机械能变化 W外＝E2－E1‎ 例7　(2017·丽水、衢州、湖州三地市质量检测)有一种大型游戏机叫“跳楼机”，如图7所示，参加游戏的游客被安全带固定在座椅上，先由电动机将座椅沿竖直轨道提升到离地面高H处，然后由静止释放．游客们的总质量为m，重力加速度为g，下列关于游客们缓慢上升的过程说法正确的是(　　)‎ 图7‎ A．合力对游客们所做的功为mgH B．游客们的重力势能增加了mgH C．电动机所做的功为mgH D．游客们的机械能守恒 答案　B 解析　游客缓慢上升过程中，可以认为速度不变，W合＝0，A错误；升高H，游客重力势能增加mgH，B正确；电动机做的功等于游客和座椅重力势能的增加量，C错误；游客的速度不变即动能不变，而重力势能增加，故游客的机械能增加，D错误.‎ ‎1．(2016·浙江10月学考·4)如图8所示，无人机在空中匀速上升时，不断增加的能量是(　　)‎ 图8‎ A．动能 B．动能、重力势能 C．重力势能、机械能 D．动能、重力势能、机械能 答案　C 解析　无人机匀速上升，所以动能保持不变，选项A、B、D均错误．高度不断增加，所以重力势能不断增加，在上升过程中升力对无人机做正功，所以无人机机械能不断增加，所以选项C正确．‎ ‎2.(2018·嘉兴市学考科目考试)如图9是一种名为“牙签弩”的玩具弓弩，现竖直向上发射木质牙签，O点为皮筋自然长度位置，A为发射的起点位置．若不计一切阻力，则(　　)‎ 图9‎ A．A到O的过程中，牙签一直处于超重状态 B．A到O的过程中，牙签的机械能守恒 C．在上升过程中，弓和皮筋的弹性势能转化为牙签的动能 D．根据牙签向上飞行的高度可测算出牙签被射出时的速度 答案　D ‎3．(2017·浙江4月学考·12)火箭发射回收是航天技术的一大进步．如图10所示，‎ 火箭在返回地面前的某段运动，可看成先匀速后减速的直线运动，最后撞落在地面上．不计火箭质量的变化，则(　　)‎ 图10‎ A．火箭在匀速下降过程中，机械能守恒 B．火箭在减速下降过程中，携带的检测仪器处于失重状态 C．火箭在减速下降过程中合力做功等于火箭机械能的变化 D．火箭着地时，火箭对地的作用力大于自身的重力 答案　D 解析　匀速下降阶段，火箭除受重力外，还受阻力，且阻力做负功，所以机械能不守恒，选项A错误；在减速阶段，加速度向上，处于超重状态，而火箭克服阻力做的功等于机械能的减少量，选项B、C错误；火箭着地时突然减速，则地面给火箭的力大于火箭的重力，根据牛顿第三定律，选项D正确．‎ ‎4．(2017·绍兴一中期末)如图11所示，在高为H的桌面上以速度v水平抛出质量为m的物体，物体落到距地面高为h处的A点，不计空气阻力且以桌面为零势能面．则下列说法正确的是(　　)‎ 图11‎ A．物体在A点的机械能为mgh＋mv2‎ B．物体在A点的机械能为mv2‎ C．物体在A点的动能为mgh＋mv2‎ D．物体在A点的动能为mg(H－h)‎ 答案　B 解析　不计空气阻力且以桌面为零势能面，物体运动过程中机械能总量为mv2，且保持不变，故A错误，B正确；物体在A点的动能为mg(H－h)＋mv2，故C、D错误．‎ ‎5.(2018·嘉兴市第一中学第二学期期中考试)如图12所示，悬崖上有一质量m＝50 kg的石块，距离地面高度h＝20 m，由于长期风化作用而从悬崖上由静止落到地面．若下落时不计空气阻力且石块质量不变，以地面为零势能面，求石块：(g取10 m/s2)‎ 图12‎ ‎(1)未下落时在悬崖上的重力势能；‎ ‎(2)落到地面时的速度大小；‎ ‎(3)落到地面时的机械能大小．‎ 答案　(1)1×104 J　(2)20 m/s　(3)1×104 J 解析　(1)以地面为零势能面，石块未下落时在悬崖上的重力势能为：Ep＝mgh＝50×10×20 J＝1×104 J.‎ ‎(2)根据机械能守恒定律可得：mv2＝mgh 代入数据得：v＝20 m/s ‎(3)因为在下落过程中只有重力做功，机械能守恒，所以落到地面时的机械能大小为1×104 J.‎ ‎6．(2016·浙江4月学考·20)如图13所示装置由一理想弹簧发射器及两个轨道组成．其中轨道Ⅰ由光滑轨道AB与粗糙直轨道BC平滑连接，高度差分别是h1＝0.20 m、h2＝0.10 m，BC水平距离L＝1.00 m．轨道Ⅱ由AE、螺旋圆形EFG和GB三段光滑轨道平滑连接而成，且A点与F点等高．当弹簧压缩量为d时，恰能使质量m＝0.05 kg的滑块沿轨道Ⅰ上升到B点；当弹簧压缩量为2d时，恰能使滑块沿轨道Ⅰ上升到C点．(已知弹簧弹性势能与压缩量的平方成正比，g＝10 m/s2)‎ 图13‎ ‎(1)当弹簧压缩量为d时，求弹簧的弹性势能及滑块离开弹簧瞬间的速度大小；‎ ‎(2)求滑块与轨道BC间的动摩擦因数；‎ ‎(3)当弹簧压缩量为d时，若沿轨道Ⅱ运动，滑块能否上升到B点？请通过计算说明理由．‎ 答案　(1)0.1 J　2 m/s　(2)0.5　(3)见解析 解析　(1)由机械能守恒定律可得 E弹＝ΔEk＝ΔEp＝mgh1＝0.05×10×0.20 J＝0.1 J 由ΔEk＝mv02，可得v0＝2 m/s ‎(2)由E弹∝d2，可得当弹簧压缩量为2d时，‎ ΔEk′＝E弹′＝4E弹＝4mgh1‎ 由动能定理可得－mg(h1＋h2)－μmgL＝－ΔEk′‎ 解得μ＝＝0.5‎ ‎(3)滑块恰能通过螺旋圆形轨道最高点需满足的条件是 mg＝ 由机械能守恒定律有v＝v0＝2 m/s 解得Rm＝0.4 m 当R>0.4 m时，滑块会脱离螺旋圆形轨道，不能上升到B点；‎ 当R≤0.4 m时，滑块能上升到B点．‎ 一、选择题 ‎1．如图1所示，下列各种运动过程中，物体(弓、过山车、石头、圆珠笔)机械能守恒的是(忽略空气阻力)(　　)‎ 图1‎ A．图甲，将箭搭在弦上，拉弓的整个过程 B．图乙，过山车在动力作用下从轨道上缓慢上行的过程 C．图丙，在一根细线的中央悬挂着一石头，双手拉着细线两端沿水平方向缓慢分开的过程 D．图丁，手握内有弹簧的圆珠笔，笔帽抵在桌面放手后圆珠笔弹起的过程 答案　D 解析　将箭搭在弦上，拉弓的整个过程，外力对弓做功，机械能增加，A错误；过山车在动力作用下从轨道上缓慢上行的过程，重力势能变大，动能不变，机械能变大，B错误；在一根细线的中央悬挂着一 石头，双手拉着细线两端沿水平方向缓慢分开的过程，石头的重力势能变大，动能不变，机械能不守恒，C错误；手握内有弹簧的圆珠笔，笔帽抵在桌面放手后圆珠笔弹起的过程，只有重力和圆珠笔内弹簧的弹力对圆珠笔做功，机械能守恒，D正确．‎ ‎2.如图2所示为跳伞爱好者表演高楼跳伞的情形，他们从楼顶跳下后，在距离地面一定高度处打开伞包，最终安全着陆，则跳伞者打开伞包至着陆过程中(　　)‎ 图2‎ A．机械能一直减小 B．机械能一直增大 C．动能一直减小 D．重力势能一直增大 答案　A 解析　由于跳伞者所受的拉力和空气阻力对跳伞者做负功，由功能关系知，跳伞者的机械能一直减小，A项正确，B项错误；动能先增大后减小，C项错误；重力一直做正功，重力势能一直减小，故D项错误．‎ ‎3.(2015·浙江10月学考·5)画作《瀑布》如图3所示．有人对此画作了如下解读：水流从高处倾泻而下，推动水轮机发电，又顺着水渠流动，回到瀑布上方，然后再次倾泻而下，如此自动地周而复始．这一解读违背了(　　)‎ 图3‎ A．库仑定律 B．欧姆定律 C．电荷守恒定律 D．能量守恒定律 答案　D ‎4.(2017·金华市十校联考)2016年巴西奥运会上，中国选手邓薇以262公斤(抓举115公斤，挺举147公斤)的总成绩打破奥运会纪录、世界纪录．如图4所示，某次抓举，在杠铃被举高的整个过程中，不计空气阻力，下列说法正确的是(　　)‎ 图4‎ A．杠铃的动能一直增大 B．杠铃的重力势能一直增大 C．杠铃的机械能守恒 D．杠铃一直处于超重状态 答案　B 解析　杠铃被举高的过程一定经历了先加速向上，后减速向上的运动，所以动能应先增大后减小，A错误；杠铃一直向上运动，重力势能一直增大，B正确；因人对杠铃的支持力做正功，杠铃的机械能增加，C错误；加速度先向上，后向下，杠铃先超重，后失重，D错误．‎ ‎5.(2017·金华市期末)如图5所示，超市为了方便顾客上楼安装了智能化的自动扶梯(无台阶)．为了节约能源，在没有顾客乘行时，自动扶梯以较小的速度匀速运行；当有顾客乘行时，自动扶梯经过先加速再匀速两个阶段运行．则电梯在运送顾客上楼的整个过程中(　　)‎ 图5‎ A．顾客始终受摩擦力作用 B．摩擦力对顾客先做正功后不做功 C．顾客对扶梯的作用力始终竖直向下 D．顾客的机械能先增大后保持不变 答案　A 解析　在自动扶梯向上加速和匀速运行过程中，顾客始终有相对电梯向下的运动趋势，所以始终受摩擦力作用，故A正确．摩擦力对顾客一直做正功，故B错误．扶梯在向上加速运行时，顾客受到沿扶梯向上的合力，根据平行四边形定则，扶梯对顾客的作用力沿扶梯向上，故顾客对扶梯的作用力沿扶梯向下；自动扶梯向上匀速运行时，由平衡条件及牛顿第三定律知，顾客对扶梯的作用力竖直向下，故C错误．顾客随着扶梯上升，顾客重力势能不断增加，动能先增加后不变，故机械能一直增加，D错误．‎ ‎6.(2018·杭西高月考)韩晓鹏是我国首位在冬奥会雪上项目夺冠的运动员．如图6，他在一次自由式滑雪空中技巧比赛中沿“助滑区”保持同一姿势下滑了一段距离，重力对他做功 ‎1 900 J，他克服阻力做功100 J．韩晓鹏在此过程中(　　)‎ 图6‎ A．动能增加了1 900 J B．动能增加了2 000 J C．重力势能减小了1 900 J D．重力势能减小了2 000 J 答案　C ‎7．(2017·杭州市期末)为了方便打开核桃、夏威夷果等坚果，有人发明了一款弹簧坚果开核器，它由锥形弹簧、固定在弹簧顶部的硬质小球及放置坚果的果垫组成．如图7所示是演示打开核桃的三个步骤，则下列说法正确的是(　　)‎ 图7‎ A．弹簧被向上拉伸的过程中，弹簧的弹性势能减小 B．松手后，小球向下运动过程中，小球的机械能守恒 C．小球向下运动过程中，弹簧对小球做正功 D．打击过程中，果垫对核桃做负功 答案　C ‎8.(2017·余杭、萧山、新登、昌化四校期中)如图8所示，一蹦极运动员身系弹性蹦极绳从水面上方的高台下落，到最低点时距水面还有数米距离．假定空气阻力可忽略，运动员可视为质点，下列说法不正确的是(　　)‎ 图8‎ A．运动员到达最低点前重力势能始终减小 B．蹦极绳张紧后的下落过程中，弹力做负功，弹性势能增加 C．蹦极过程中，运动员、地球和蹦极绳所组成的系统机械能守恒 D．蹦极过程中，重力势能的改变量与重力势能零点的选取有关 答案　D ‎9.(2017·温州市学考模拟)抽水蓄能电站的工作原理是：在用电低谷时，电站利用电网多余电能把水抽到高处蓄水池中，到用电高峰时，再利用蓄水池中的水发电．浙江天荒坪抽水蓄能电站是亚洲第一大高山蓄能水电站，堪称世纪之作．山顶水库面积达2.8×105 m2(水库近似为长方体)，已知上、下水库落差H＝600 m，如图9所示．蓄水后一昼夜连续发电，山顶水库水位降低30 m，若水的重力势能80%转化为电能，水的密度为1.0×103 kg/m3，g取10 m/s2.则一个昼夜连续发电所产生的电能约为(　　)‎ 图9‎ A．4×1010 J B．4×1011 J C．4×1012 J D．4×1013 J 答案　D 解析　山顶水库水位降低30 m的水的体积V＝Sh＝2.8×105×30 m3＝8.4×106 m3，其质量m＝ρV＝8.4×109 kg，水减少的重力势能ΔEp＝mgH＝8.4×109×10×600 J＝5.04×1013 J，转化的电能E电＝80%ΔEp≈4×1013 J，所以应选D.‎ ‎10．(2015·浙江10月学考·8)质量为30 kg的小孩坐在秋千板上，秋千板离系绳子的横梁的距离是2.5 m．小孩的父亲将秋千板从最低点拉起1.25 m高度后由静止释放，小孩沿圆弧运动至最低点时，她对秋千板的压力约为(g取10 m/s2，不计空气阻力)(　　)‎ A．0 B．200 N C．600 N D．1 000 N 答案　C 解析　由题意知秋千板和小孩组成的系统的机械能守恒，取最低点为零势能参考平面，则由机械能守恒定律得 ‎(M＋m)gh＝(M＋m)v2‎ 得v＝ 对小孩在最低点有 FN－mg＝m 解得FN＝600 N 由牛顿第三定律知，她对秋千板的压力大小为600 N.‎ ‎11．(2018·浙江名校协作体期末)弹弓是孩子们喜爱的弹射类玩具，其构造原理如图10所示，橡皮筋两端点A、B固定在把手上，橡皮筋处于ACB时恰好为原长状态，在C处(AB连线的中垂线上)放一固体弹丸，一手执把，另一手将弹丸拉至D点放手，弹丸就会在橡皮筋的作用下发射出去，击中目标．现将弹丸竖直向上发射，已知E是CD中点，则(　　)‎ 图10‎ A．从D到C过程中，弹丸的机械能守恒 B．从D到C过程中，弹丸的动能一直在增大 C．从D到C过程中，橡皮筋的弹性势能先增大后减小 D．从D到E过程中，橡皮筋对弹丸做的功大于从E到C过程橡皮筋对弹丸做的功 答案　D 解析　从D到C过程中，橡皮筋对弹丸做正功，弹丸的机械能增加，选项A错误；从D到C过程中，弹丸的动能先增大后减小，选项B错误；从D到C过程中，橡皮筋的弹性势能一直减小，选项C错误；从D到E过程中，橡皮筋对弹丸的弹力大于从E到C过程中橡皮筋对弹丸的弹力，故从D到E过程橡皮筋对弹丸做的功大于从E到C过程橡皮筋对弹丸做的功，选项D正确．‎ 二、非选择题 ‎12．(2017·嘉兴市第一中学第二学期期中考试)如图11所示为马戏团的猴子表演杂技示意图．平台上质量为5 kg的猴子(可视为质点)从平台边缘A点抓住长l＝0.8 m水平绳的末端，由静止开始绕绳的另一个固定端O点做圆周运动，运动至O点正下方B点时松开绳子，之后做平抛运动．在B点右侧平地上固定一个倾角为37°的斜面滑梯CD，猴子做平抛运动至斜面的最高点C时的速度方向恰好沿斜面方向．已知sin 37°＝0.6，cos 37°＝0.8，求：(g取10 m/s2)‎ 图11‎ ‎(1)猴子刚运动到B点时的速度大小；‎ ‎(2)猴子刚运动到B点且绳子还未脱手时，其对绳子的拉力；‎ ‎(3)猴子从B点运动到C点的时间以及BC两点间的水平距离．‎ 答案　(1)4 m/s　(2)150 N，方向竖直向下　(3)0.3 s　1.2 m 解析　(1)设猴子在B点的速度为v，由A到B的过程中，由机械能守恒定律得mgl＝mv2‎ 代入数据得：v＝4 m/s ‎(2)设在B点时猴子所受的拉力为F，由牛顿第二定律得：F－mg＝m 联立解得：F＝150 N 由牛顿第三定律得：猴子拉绳的力等于绳拉猴子的力，大小等于150 N，方向竖直向下．‎ ‎(3)据题得：猴子到达C点时竖直分速度vy＝vtan 37°＝3 m/s 平抛运动的时间t＝＝ s＝0.3 s BC间的水平距离x＝vt＝1.2 m.‎ ‎13．(2018·丽水、衢州、湖州三地市教学质量检测)图12甲为风火轮惯性轨道极限跳跃赛道，其模型可以简化为图乙．整个装置由直轨道AB、半径R1＝15 cm的竖直螺旋圆轨道BO′B′、半径R2＝30 cm的圆弧轨道B′C′，以及右侧可移动得分框组成，轨道各部分均光滑．已知比赛过程所用小车(可视为质点)质量m＝0.04 kg，g＝10 m/s2，∠C′O′B′＝37°，sin 37°＝0.6，cos 37°＝0.8.求：‎ 图12‎ ‎(1)小车恰好通过竖直圆轨道最高点的速度大小；‎ ‎(2)若小车在C′处的速度为3 m/s，求小车经过B′时对轨道的压力大小；‎ ‎(3)若改变v0，且每次小车离开C′后能水平进入得分框，求得分框的离地高度H与该得分框与C′的水平距离x之间的函数关系式(可能用到≈2.5)．‎ 答案　见解析 解析　(1)若小车恰好经过最高点，有mg＝m 解得：v＝ m/s＝ m/s ‎(2)由几何关系可知：ΔhB′C′＝R2(1－cos 37°)‎ 小车从B′到C′由机械能守恒定律得：mvB′2＝mvC′2＋mgΔhB′C′‎ 在B′处由牛顿第二定律有FNB′－mg＝m 联立可得FNB′＝1.76 N 由牛顿第三定律知在B′处时小车对轨道压力大小为1.76 N ‎(3)若小车恰能经过最高点O′点，‎ 从O′到C′，由机械能守恒定律得：mv2＋mgΔhO′C′＝mv 又ΔhO′C′＝R2cos 37°‎ 解得vC′＝ m/s≈2.5 m/s 此时，有xmin＝vC′cos 37°·≈0.3 m 若使小车恰能水平进入得分框，根据平抛运动的物体在任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点，有：‎ H－ΔhB′C′＝tan 37°· 解得H＝x＋0.06 (m)，x≥0.3 m.‎