2008年广东省高考数学试卷（理科）【附答案、word版本，可再编辑；B4纸型两栏】 7页

1 / 7 2008 年广东省高考数学试卷（理科） 一、选择题（共 8 小题，每小题 5 分，满分 40 分） 1. 已知0 < 푎 < 2，复数푧的实部为푎，虚部为1，则|푧|的取值范围是（ ） A.(1, 5) B.(1, 3) C.(1, 5) D.(1, 3) 2. 等差数列{푎푛}的前푛项和为푆푛，若푎1 = 1 2，푆4 = 20，则푆6 = ( ) A.16 B.24 C.36 D.48 3. 某校共有学生2000名，各年级男、女生人数如下表．已知在全校学生 中随机抽取1名，抽到二年级女生的概率是0.19．现用分层抽样的方法在全 校抽取64名学生，则应在三年级抽取的学生人数为（ ） 一年级 二年级 三年级 女生 373 푥 푦 男生 377 370 푧 A.24 B.18 C.16 D.12 4. 若变量푥，푦满足{2푥 + 푦 ≤ 40 푥 + 2푦 ≤ 50 푥 ≥ 0 푦 ≥ 0  则푧＝3푥 +2푦的最大值是（ ） A.90 B.80 C.70 D.40 5. 将正三棱柱截去三个角（如图1所示퐴，퐵，퐶分别是 △ 퐺퐻퐼三边的中点） 得到几何体如图2，则该几何体按图2所示方向的侧视图（或称左视图）为 （ ） A. B. C. D. 6. 已知命题푝：所有有理数都是实数，命题푞：正数的对数都是负数，则 下列命题中为真命题的是（ ） A.(￢푝) ∨ 푞 B.푝 ∧ 푞 C.(￢푝) ∧ (￢푞) D.(￢푝) ∨ (￢푞) 7. 设푎 ∈ R，若函数푦 = 푒푎푥 +3푥，푥 ∈ R有大于零的极值点，则( ) A.푎 > ―3 B.푎 < ―3 C.푎 > ― 1 3 D.푎 < ― 1 3 8. 在平行四边形퐴퐵퐶퐷中，퐴퐶与퐵퐷相交于点푂，퐸是线段푂퐷的中点，퐴퐸 的延长线与퐶퐷交于点퐹．若 → 퐴퐶 = → 푎， → 퐵퐷 = → 푏，则 → 퐴퐹等于( ) A.1 4 → 푎 + 1 2 → 푏 B.2 3 → 푎 + 1 3 → 푏 C.1 2 → 푎 + 1 4 → 푏 D.1 3 → 푎 + 2 3 → 푏 二、填空题（共 7 小题，9--12 为必做题。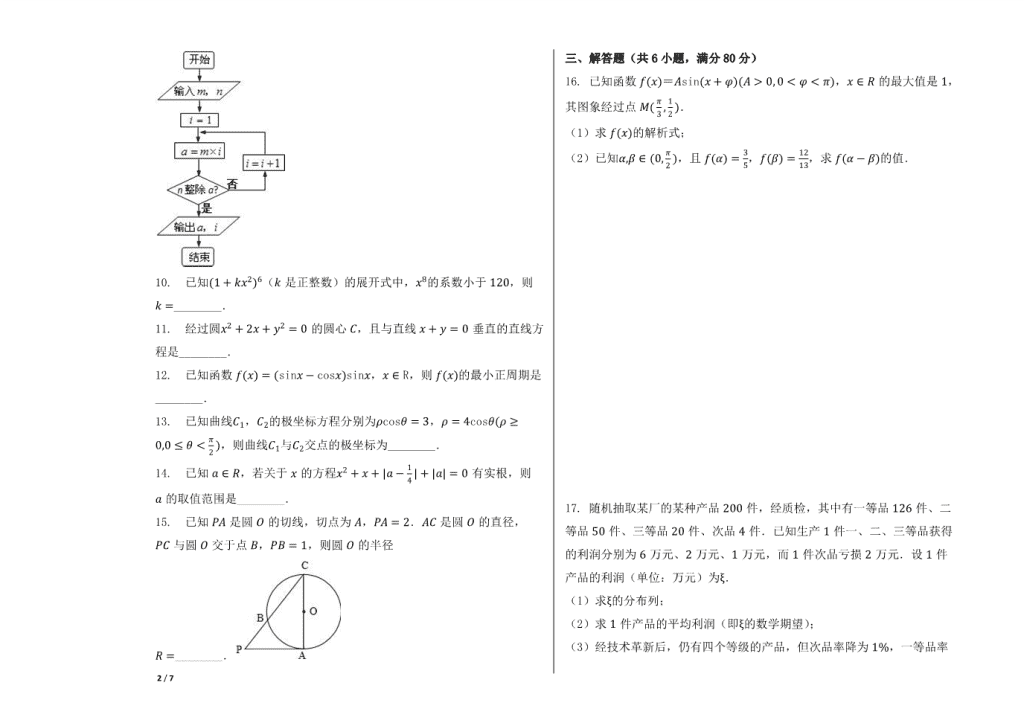13--15 题选其中两道题，每小 题 5 分，满分 30 分） 9. 阅读程序框图，若输入푚 = 4，푛 = 3，则输出푎 = ________，푖 = ________． （注：框图中的赋值符号“ = ”，也可以写成“←”或“： = ”） 2 / 7 10. 已知(1 + 푘푥2)6（푘是正整数）的展开式中，푥8的系数小于120，则푘 = ________． 11. 经过圆푥2 +2푥 + 푦2 = 0的圆心퐶，且与直线푥 + 푦 = 0垂直的直线方程 是________． 12. 已知函数푓(푥) = (sin푥 ― cos푥)sin푥，푥 ∈ R，则푓(푥)的最小正周期是 ________． 13. 已知曲线퐶1，퐶2的极坐标方程分别为휌cos휃 = 3，휌 = 4cos휃(휌 ≥ 0 ,0 ≤ 휃 < 휋 2)，则曲线퐶1与퐶2交点的极坐标为________． 14. 已知푎 ∈ 푅，若关于푥的方程푥2 + 푥 +|푎 ― 1 4| + |푎| = 0有实根，则푎的取 值范围是________． 15. 已知푃퐴是圆푂的切线，切点为퐴，푃퐴 = 2．퐴퐶是圆푂的直径，푃퐶与圆 푂交于点퐵，푃퐵 = 1，则圆푂的半径푅 = ________． 三、解答题（共 6 小题，满分 80 分） 16. 已知函数푓(푥)＝퐴sin(푥 + 휑)(퐴 > 0, 0 < 휑 < 휋)，푥 ∈ 푅的最大值是1， 其图象经过点푀(휋 3,1 2)． （1）求푓(푥)的解析式； （2）已知훼,훽 ∈ (0,휋 2)，且푓(훼) = 3 5，푓(훽) = 12 13，求푓(훼 ― 훽)的值． 17. 随机抽取某厂的某种产品200件，经质检，其中有一等品126件、二等 品50件、三等品20件、次品4件．已知生产1件一、二、三等品获得的利润 分别为6万元、2万元、1万元，而1件次品亏损2万元．设1件产品的利润 （单位：万元）为휉． （1）求휉的分布列； （2）求1件产品的平均利润（即휉的数学期望）； （3）经技术革新后，仍有四个等级的产品，但次品率降为1%，一等品率 3 / 7 提高为70%．如果此时要求1件产品的平均利润不小于4.73万元，则三等品 率最多是多少？ 18. 设푏 > 0，椭圆方程为 푥2 2푏2 + 푦2 푏2 = 1，抛物线方程为푥2 = 8(푦 ― 푏)．如图 所示，过点퐹(0, 푏 +2)作푥轴的平行线，与抛物线在第一象限的交点为퐺，已 知抛物线在点퐺的切线经过椭圆的右焦点퐹1． （1）求满足条件的椭圆方程和抛物线方程； （2）设퐴，퐵分别是椭圆长轴的左、右端点，试探究在抛物线上是否存在 点푃，使得 △ 퐴퐵푃为直角三角形？若存在，请指出共有几个这样的点？并 说明理由（不必具体求出这些点的坐标）． 19. 设푘 ∈ 푅，函数푓(푥) = { 1 1 ― 푥 푥 < 1 ― 푥 ― 1 푥 ≥ 1 ，퐹(푥) = 푓(푥) ― 푘푥，푥 ∈ 푅， 试讨论函数퐹(푥)的单调性． 20. 如图所示，四棱锥푃 ― 퐴퐵퐶퐷的底面퐴퐵퐶퐷是半径为푅的圆的内接四边形， 其中퐵퐷是圆的直径，∠퐴퐵퐷 = 60∘，∠퐵퐷퐶 = 45∘，푃퐷垂直底面퐴퐵퐶퐷，푃퐷 4 / 7 = 2 2푅，퐸，퐹分别是푃퐵，퐶퐷上的点，且푃퐸 퐸퐵 = 퐷퐹 퐹퐶，过点퐸作퐵퐶的平行线交 푃퐶于퐺． （1）求퐵퐷与平面퐴퐵푃所成角휃的正弦值； （2）证明： △ 퐸퐹퐺是直角三角形； （3）当푃퐸 퐸퐵 = 1 2时，求 △ 퐸퐹퐺的面积． 21. 设푝，푞为实数，훼，훽是方程푥2 ― 푝푥 + 푞 = 0的两个实根，数列{푥푛}满 足푥1 = 푝，푥2 = 푝2 ― 푞，푥푛 = 푝푥푛―1 ― 푞푥푛―2(푛 = 3, 4,…)． （1）证明：훼 + 훽 = 푝，훼훽 = 푞； （2）求数列{푥푛}的通项公式； （3）若푝 = 1，푞 = 1 4，求{푥푛}的前푛项和푆푛． 5 / 7 参考答案与试题解析 2008 年广东省高考数学试卷（理科） 一、选择题（共 8 小题，每小题 5 分，满分 40 分） 1.C 2.D 3.C 4.C 5.A 6.D 7.B 8.B 二、填空题（共 7 小题，9--12 为必做题。13--15 题选其中两道题，每小 题 5 分，满分 30 分） 9.12,3 10.1 11.푥 ― 푦 +1 = 0 12.휋 13.(2 3，휋 6) 14.[0,1 4] 15. 3 三、解答题（共 6 小题，满分 80 分） 16.依题意有퐴＝1，则푓(푥)＝sin(푥 + 휑)，将点푀(휋 3,1 2)代入得sin(휋 3 + 휑) = 1 2， 而0 < 휑 < 휋，∴ 휋 3 + 휑 = 5 6휋，∴ 휑 = 휋 2，故푓(푥) = sin(푥 + 휋 2) = cos푥． 依题意有cos훼 = 3 5,cos훽 = 12 13，而훼,훽 ∈ (0,휋 2)，∴ sin훼 = 1 ― (3 5) 2 = 4 5,sin 훽 = 1 ― (12 13) 2 = 5 13，푓(훼 ― 훽) = cos(훼 ― 훽) = cos훼cos훽 + sin훼sin훽 = 3 5 × 12 13 + 4 5 × 5 13 = 56 65． 17.解：휉的所有可能取值有6，2，1， ― 2；푃(휉 = 6) = 126 200 = 0.63，푃(휉 = 2) = 50 200 = 0.25푃(휉 = 1) = 20 200 = 0.1，푃(휉 = ―2) = 4 200 = 0.02 故휉的分布列为： 휉 6 2 1 ―2 푃 0.63 0.25 0.1 0.02 （2）퐸휉 = 6 × 0.63 + 2 × 0.25 + 1 × 0.1 + ( ― 2) × 0.02 = 4.34 （3）设技术革新后的三等品率为푥，则此时1件产品的平均利润为퐸(푥 ) = 6 × 0.7 + 2 × (1 ― 0.7 ― 0.01 ― 푥) + 1 × 푥 +( ― 2) × 0.01 = 4.76 ― 푥 (0 ≤ 푥 ≤ 0.29) 依题意，퐸(푥) ≥ 4.73，即4.76 ― 푥 ≥ 4.73，解得푥 ≤ 0.03所以三等品率最多 为3% 18.解：（1）由푥2 = 8(푦 ― 푏)得푦 = 1 8푥2 + 푏， 当푦 = 푏 +2得푥 =± 4，∴ 퐺点的坐标为(4, 푏 +2)，푦′ = 1 4푥，푦′|푥=4 = 1， 过点퐺的切线方程为푦 ― (푏 +2) = 푥 ― 4即푦 = 푥 + 푏 ― 2， 令푦 = 0得푥 = 2 ― 푏，∴ 퐹1点的坐标为(2 ― 푏, 0)，由椭圆方程得퐹1点的 坐标为(푏, 0)， ∴ 2 ― 푏 = 푏即푏 = 1，即椭圆和抛物线的方程分别为푥2 2 + 푦2 = 1和푥2 = 8( 푦 ― 1)； （2）∵ 过퐴作푥轴的垂线与抛物线只有一个交点푃，∴ 以∠푃퐴퐵为直 角的푅푡 △ 퐴퐵푃只有一个， 同理∴ 以∠푃퐵퐴为直角的푅푡 △ 퐴퐵푃只有一个； 若以∠퐴푃퐵为直角，则点푃在以퐴퐵为直径的圆上，而以퐴퐵为直径的圆与抛 物线有两个交点． 所以，以∠퐴푃퐵为直角的푅푡 △ 퐴퐵푃有两个； 因此抛物线上存在四个点使得 △ 퐴퐵푃为直角三角形． 6 / 7 19.解： 퐹(푥) = 푓(푥) ― 푘푥 = { 1 1 ― 푥 ― 푘푥 푥 < 1 ― 푥 ― 1 ― 푘푥 푥 ≥ 1 퐹′(푥) = { 1 (1 ― 푥)2 ― 푘 푥 < 1 ― 1 2 푥 ― 1 ― 푘 푥 ≥ 1 对于퐹(푥) = 1 1 ― 푥 ― 푘푥(푥 < 1)， 当푘 ≤ 0时，函数퐹(푥)在( ― ∞, 1)上是增函数； 当푘 > 0时，函数퐹(푥)在( ― ∞,1 ― 1 푘)上是减函数，在(1 ― 1 푘，1)上是增函 数； 对于퐹(푥) = ― 1 2 푥 ― 1 ― 푘(푥 ≥ 1)， 当푘 ≥ 0时，函数퐹(푥)在[1,  + ∞)上是减函数； 当푘 < 0时，函数퐹(푥)在[1,1 + 1 4푘2)上是减函数，在[1 + 1 4푘2， +∞)上是增函 数． 20.解：（1）在푅푡 △ 퐵퐴퐷中，∵ ∠퐴퐵퐷 = 60∘，∴ 퐴퐵 = 푅,퐴퐷 = 3푅 而푃퐷垂直底面퐴퐵퐶퐷， 푃퐴 = 푃퐷2 + 퐴퐷2 = (2 2푅)2 + ( 3푅)2 = 11푅， 푃퐵 = 푃퐷2 + 퐵퐷2 = (2 2푅)2 + (2푅)2 = 2 3푅， 在 △ 푃퐴퐵中，푃퐴2 + 퐴퐵2 = 푃퐵2，即 △ 푃퐴퐵为以∠푃퐴퐵为直角的直角三角形． 设点퐷到面푃퐴퐵的距离为퐻，由푉푃―퐴퐵퐷 = 푉퐷―푃퐴퐵，有푃퐴 ⋅ 퐴퐵 ⋅ 퐻 = 퐴퐵 ⋅ 퐴퐷 ⋅ 푃퐷， 即퐻 = 퐴퐷 ⋅ 푃퐷 푃퐴 = 3푅 ⋅ 2 2푅 11푅 = 2 66 11 푅，sin휃 = 퐻 퐵퐷 = 66 11 ． （2）퐸퐺 // 퐵퐶，∴ 푃퐸 퐸퐵 = 푃퐺 퐺퐶，而푃퐸 퐸퐵 = 퐷퐹 퐹퐶，即푃퐺 퐺퐶 = 퐷퐹 퐹퐶， ∴ 퐺퐹 // 푃퐷，∴ 퐺퐹 ⊥ 퐵퐶，∴ 퐺퐹 ⊥ 퐸퐺，∴ △ 퐸퐹퐺是直角三角 形． （3）푃퐸 퐸퐵 = 1 2时퐸퐺 퐵퐶 = 푃퐸 푃퐵 = 1 3，퐺퐹 푃퐷 = 퐶퐹 퐶퐷 = 2 3， 即퐸퐺 = 1 3퐵퐶 = 1 3 × 2푅 × cos45∘ = 2 3 푅，퐺퐹 = 2 3푃퐷 = 2 3 × 2 2푅 = 4 2 3 푅， ∴ △ 퐸퐹퐺的面积푆△퐸퐹퐺 = 1 2퐸퐺 ⋅ 퐺퐹 = 1 2 × 2 3 푅 × 4 2 3 푅 = 4 9푅2． 21.解：（1）由求根公式，不妨设훼 < 훽，得훼 = 푝 ― 푝2 ― 4푞 2 ，훽 = 푝 + 푝2 ― 4푞 2 ∴ 훼 + 훽 = 푝 ― 푝2 ― 4푞 2 + 푝 + 푝2 ― 4푞 2 = 푝， 훼훽 = 푝 ― 푝2 ― 4푞 2 × 푝 + 푝2 ― 4푞 2 = 푞． （2）设푥푛 ― 푠푥푛―1 = 푡(푥푛―1 ― 푠푥푛―2)，则푥푛 = (푠 + 푡)푥푛―1 ― 푠푡푥푛―2，由푥푛 = 푝푥푛―1 ― 푞푥푛―2 得{푠 + 푡 = 푝 푠푡 = 푞 ， 消去푡，得푠2 ― 푝푠 + 푞 = 0， ∴ 푠是方程푥2 ― 푝푥 + 푞 = 0的根，由题意可知，푠1 = 훼，푠2 = 훽 ①当훼 ≠ 훽时，此时方程组{푠 + 푡 = 푝 푠푡 = 푞 的解为{푠1 = 훼 푡1 = 훽或{푠2 = 훽 푡2 = 훼 ∴ 푥푛 ― 훼푥푛―1 = 훽(푥푛―1 ― 훼푥푛―2)，푥푛 ― 훽푥푛―1 = 훼(푥푛―1 ― 훽푥푛―2)， 即{푥푛 ― 푡1푥푛―1}、{푥푛 ― 푡2푥푛―1}分别是公比为푠1 = 훼、푠2 = 훽的等比数列， 由等比数列性质可得푥푛 ― 훼푥푛―1 = (푥2 ― 훼푥1)훽푛―2，푥푛 ― 훽푥푛―1 = (푥2 ― 훽푥1) 훼푛―2， 两式相减，得(훽 ― 훼)푥푛―1 = (푥2 ― 훼푥1)훽푛―2 ― (푥2 ― 훽푥1)훼푛―2 ∵ 푥2 = 푝2 ― 푞，푥1 = 푝， ∴ 푥2 = 훼2 + 훽2 + 훼훽，푥1 = 훼 + 훽 ∴ (푥2 ― 훼푥1)훽푛―2 = 훽2 ⋅ 훽푛―2 = 훽푛，(푥2 ― 훽푥1)훼푛―2 = 훼2 ⋅ 훼푛―2 = 훼푛 ∴ (훽 ― 훼)푥푛―1 = 훽푛 ― 훼푛， 即∴ 푥푛―1 = 훽푛 ― 훼푛 훽 ― 훼 ，∴ 푥푛 = 훽푛+1 ― 훼푛+1 훽 ― 훼 7 / 7 ②当훼 = 훽时，即方程푥2 ― 푝푥 + 푞 = 0有重根，∴ 푝2 ― 4푞 = 0， 即(푠 + 푡)2 ― 4푠푡 = 0，得(푠 ― 푡)2 = 0， ∴ 푠 = 푡，不妨设푠 = 푡 = 훼，由①可知푥푛 ― 훼푥푛―1 = (푥2 ― 훼푥1)훽푛―2， ∵ 훼 = 훽，∴ 푥푛 ― 훼푥푛―1 = (푥2 ― 훼푥1)훼푛―2 = 훼푛 即∴ 푥푛 = 훼푥푛―1 + 훼푛，等式两边同时除以훼푛， 得푥푛 훼푛 = 푥푛―1 훼푛―1 +1， 即푥푛 훼푛 ― 푥푛―1 훼푛―1 = 1 ∴ 数列{ 푥푛 훼푛}是以1为公差的等差数列， ∴ 푥푛 훼푛 = 푥1 훼 +(푛 ― 1) × 1 = 2훼 훼 + 푛 ― 1 = 푛 +1， ∴ 푥푛 = 푛훼푛 + 훼푛 综上所述，푥푛 = {훽푛+1 ― 훼푛+1 훽 ― 훼 ，(훼 ≠ 훽) 푛훼푛 + 훼푛，(훼 = 훽) ． （3）把푝 = 1，푞 = 1 4代入푥2 ― 푝푥 + 푞 = 0，得푥2 ― 푥 + 1 4 = 0，解得훼 = 훽 = 1 2， ∴ 푥푛 = 푛 ⋅ (1 2)푛 +(1 2)푛． 푆푛 = ((1 2) + (1 2)2 +(1 2)3 +… + (1 2)푛) + ((1 2) + 2 ⋅ (1 2)2 +3 ⋅ (1 2)3 +… + 푛 ⋅ (1 2)푛)， = 1 ― (1 2)푛 +((1 2) + 2 ⋅ (1 2)2 +3 ⋅ (1 2)3 +… + 푛 ⋅ (1 2)푛) = 1 ― (1 2)푛 +2 ― (1 2)푛―1 ― 푛(1 2)푛 = 3 ― (푛 +3)(1 2)푛．