【数学】2018届一轮复习北师大版第五章数列第二节等差数列教案 9页

第二节　等差数列 ‎☆☆☆2017考纲考题考情☆☆☆‎ 考纲要求 真题举例 命题角度 ‎1.理解等差数列的概念；‎ ‎2.掌握等差数列的通项公式与前n项和公式；‎ ‎3.能在具体的问题情境中识别数列的等差关系，并能用有关知识解决相应的问题；‎ ‎4.了解等差数列与一次函数、二次函数的关系。‎ ‎2016，全国卷Ⅰ，3,5分(等差数列基本量的计算)‎ ‎2016，全国卷Ⅱ，17,12分(等差数列通项公式、求和)‎ ‎2016，北京卷，12,5分(等差数列的基本量计算)‎ ‎2016，浙江卷，6,5分(等差数列的创新应用)‎ ‎1.以考查等差数列的通项、前n项和及性质为主，等差数列的证明也是考查的热点；‎ ‎2.题型主要以选择题、填空题的形式考查等差数列的基本运算与简单性质。解答题往往与等比数列、数列求和、不等式等问题综合考查。‎ 微知识　小题练 自|主|排|查 ‎1．等差数列的有关概念 ‎(1)等差数列的定义 一般地，如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，那么这个数列就叫做等差数列，这个常数叫做等差数列的公差，通常用字母d表示，定义表达式为an－an－1＝d(常数)(n∈N*，n≥2)或an＋1－an＝d(常数)(n∈N*)。‎ ‎(2)等差中项 若三个数a，A，b成等差数列，则A叫做a与b的等差中项，且有A＝。‎ ‎2．等差数列的有关公式 ‎(1)等差数列的通项公式 如果等差数列{an}的首项为a1，公差为d，那么它的通项公式是an＝a1＋(n－1)d。‎ ‎(2)等差数列的前n项和公式 设等差数列{an}的公差为d，其前n项和Sn＝na1＋d或Sn＝。‎ ‎3．等差数列的常用性质 ‎(1)通项公式的推广：an＝am＋(n－m)d(n，m∈N*)。‎ ‎(2)若{an}为等差数列，且k＋l＝m＋n(k，l，m，n∈N*)，则ak＋al＝am＋an。‎ ‎(3)若{an}是等差数列，公差为d，则{a2n}也是等差数列，公差为2d。‎ ‎(4)若{an}，{bn}是等差数列，公差为d，则{pan＋qbn}也是等差数列。‎ ‎(5)若{an}是等差数列，公差为d，则ak，ak＋m，ak＋‎2m，…(k，m∈N*)是公差为md的等差数列。‎ ‎(6)数列Sm，S‎2m－Sm，S‎3m－S‎2m，…也是等差数列。‎ ‎(7)S2n－1＝(2n－1)an。‎ ‎(8)若n为偶数，则S偶－S奇＝；‎ 若n为奇数，则S奇－S偶＝a中(中间项)。‎ 微点提醒 ‎1．用等差数列的定义判断数列是否为等差数列，要注意定义中的三个关键词：“从第2项起”“每一项与它的前一项的差”“同一个常数”。‎ ‎2．等差数列的前n项和公式有两种表达形式，要根据题目给出的条件判断使用哪一种表达形式。‎ ‎3．等差数列与函数的关系：‎ ‎(1)通项公式：当公差d≠0时，等差数列的通项公式an＝a1＋(n－1)d＝dn＋a1－d是关于n的一次函数，且斜率为公差d。若公差d>0，则为递增数列，若公差d<0，则为递减数列。‎ ‎(2)前n项和：当公差d≠0时，Sn＝na1＋d＝n2＋n是关于n的二次函数且常数项为0。‎ 小|题|快|练 一 、走进教材 ‎1．(必修5P38例1改编)已知等差数列－5，－2,1，…，则该数列的第20项为________。‎ ‎【解析】　依题意得，该等差数列的首项为－5，公差为3，所以a20＝－5＋19×3＝52，故第20项为52。‎ ‎【答案】　52‎ ‎2．(必修5P46B组T2改编)若某等差数列的前n项和、前2n项和、前3n项和分别是A，B，C，则A、B、C之间的关系是________。‎ ‎【解析】　在等差数列中，Sn，S2n－Sn，S3n－S2n也成等差数列，即A，B－A，C－B也成等差数列，即2(B－A)＝A＋(C－B)，所以C＝3(B－A)。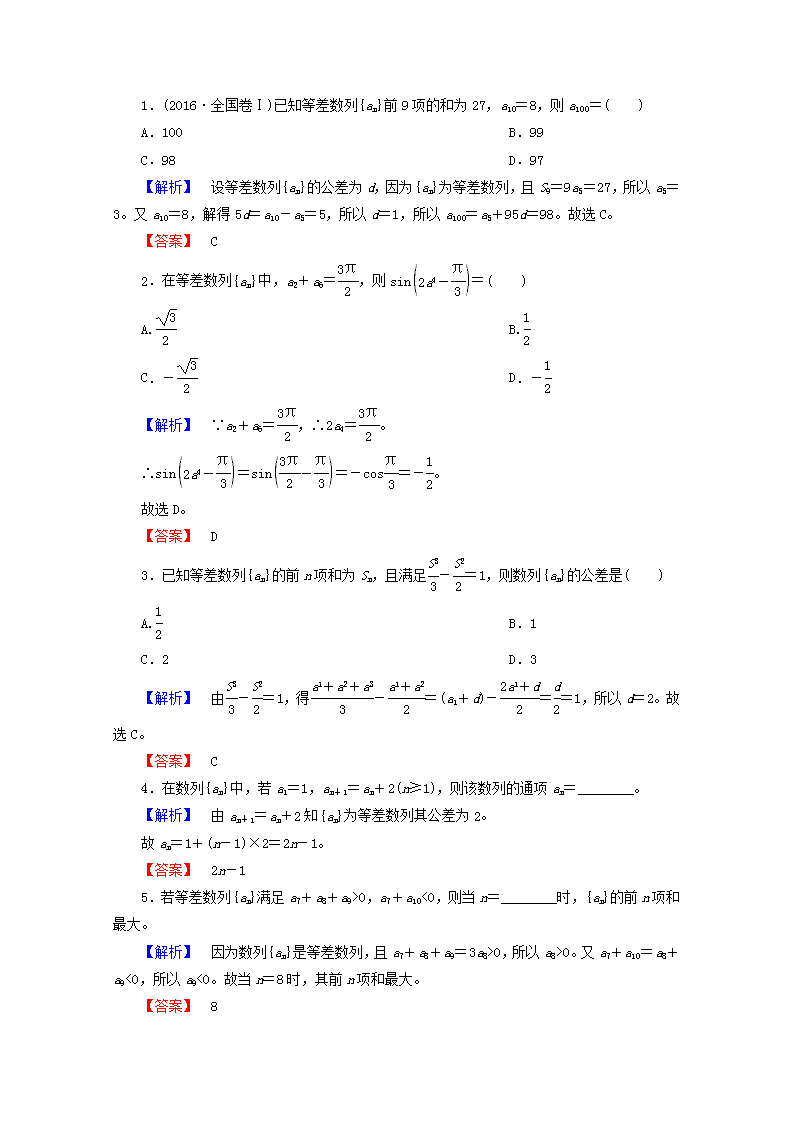‎ ‎【答案】　C＝3(B－A)‎ 二、双基查验 ‎1．(2016·全国卷Ⅰ)已知等差数列{an}前9项的和为27，a10＝8，则a100＝(　　)‎ A．100 B．99‎ C．98 D．97‎ ‎【解析】　设等差数列{an}的公差为d，因为{an}为等差数列，且S9＝‎9a5＝27，所以a5＝3。又a10＝8，解得5d＝a10－a5＝5，所以d＝1，所以a100＝a5＋95d＝98。故选C。‎ ‎【答案】　C ‎2．在等差数列{an}中，a2＋a6＝，则sin＝(　　)‎ A. B. C．－ D．－ ‎【解析】　∵a2＋a6＝，∴‎2a4＝。‎ ‎∴sin＝sin＝－cos＝－。‎ 故选D。‎ ‎【答案】　D ‎3．已知等差数列{an}的前n项和为Sn，且满足－＝1，则数列{an}的公差是(　　)‎ A. B．1‎ C．2 D．3‎ ‎【解析】　由－＝1，得－＝(a1＋d)－＝＝1，所以d＝2。故选C。‎ ‎【答案】　C ‎4．在数列{an}中，若a1＝1，an＋1＝an＋2(n≥1)，则该数列的通项an＝________。‎ ‎【解析】　由an＋1＝an＋2知{an}为等差数列其公差为2。‎ 故an＝1＋(n－1)×2＝2n－1。‎ ‎【答案】　2n－1‎ ‎5．若等差数列{an}满足a7＋a8＋a9>0，a7＋a10<0，则当n＝________时，{an}的前n项和最大。‎ ‎【解析】　因为数列{an}是等差数列，且a7＋a8＋a9＝‎3a8>0，所以a8>0。又a7＋a10＝a8＋a9<0，所以a9<0。故当n＝8时，其前n项和最大。‎ ‎【答案】　8‎ 微考点　大课堂 考点一 ‎ 等差数列的基本运算 ‎【典例1】　(2016·广州联考)已知等差数列{an}的前n项和为Sn，且a3＋a6＝4，S5＝－5。‎ ‎(1)求数列{an}的通项公式；‎ ‎(2)若Tn＝|a1|＋|a2|＋|a3|＋…＋|an|，求T5的值和Tn的表达式。‎ ‎【解析】　(1)设等差数列{an}的公差为d，由题意知，解得，故an＝2n－7(n∈N*)。‎ ‎(2)由an＝2n－7<0，得n<，即n≤3，‎ 所以当n≤3时，an＝2n－7<0，当n≥4时，an＝2n－7>0。‎ 易知Sn＝n2－6n，S3＝－9，S5＝－5，‎ 所以T5＝－(a1＋a2＋a3)＋a4＋a5＝－S3＋(S5－S3)＝S5－2S3＝13。‎ 当n≤3时，Tn＝－Sn＝6n－n2；‎ 当n≥4时，Tn＝－S3＋(Sn－S3)＝Sn－2S3＝n2－6n＋18。‎ 故Tn＝ ‎【答案】　(1)an＝2n－7(n∈N*)　(2)T5＝13‎ Tn＝ 反思归纳　1.等差数列运算问题的一般求法是设出首项a1和公差d，然后由通项公式或前n项和公式转化为方程(组)求解。‎ ‎2．等差数列的通项公式及前n项和公式共涉及五个量a1，an，d，n，Sn，已知其中三个就能求出另外两个，体现了用方程组解决问题的思想。‎ ‎【变式训练】　(1)(2016·北京高考)已知{an}为等差数列，Sn为其前n项和。若a1＝6，a3＋a5＝0，则S6＝________。‎ ‎(2)(2016·江苏高考)已知{an}是等差数列，Sn是其前n项和。若a1＋a＝－3，S5＝10，则a9的值是________。‎ ‎【解析】　(1)设等差数列{an}的公差为d，由已知得解得所以S6＝‎6a1＋×6×5d＝36＋15×(－2)＝6。‎ ‎(2)设等差数列{an}的公差为d，则a1＋a＝a1＋(a1＋d)2＝－3，S5＝‎5a1＋10d＝10，解得a1＝－4，d＝3，则a9＝a1＋8d＝－4＋24＝20。‎ ‎【答案】　(1)6　(2)20‎ 考点二 ‎ 等差数列的判定与证明 ‎【典例2】　(2017·兰州模拟)已知数列{an}中，a1＝，an＝2－(n≥2，n∈N*)，数列{bn}满足bn＝(n∈N*)。‎ ‎(1)求证：数列{bn}是等差数列；‎ ‎(2)求数列{an}中的通项公式an。‎ ‎【解析】　(1)证明：因为an＝2－(n≥2，n∈N*)，‎ bn＝。‎ 所以n≥2时，bn－bn－1＝－＝－＝－＝1。‎ 又b1＝＝－，‎ 所以数列{bn}是以－为首项，1为公差的等差数列。‎ ‎(2)由(1)知，bn＝n－，则an＝1＋＝1＋。‎ ‎【答案】　(1)数列{bn}是以－为首项，1为公差的等差数列　(2)an＝1＋ 反思归纳　等差数列的四种判断方法：‎ ‎(1)定义法：an＋1－an＝d(d是常数)⇔{an}是等差数列。‎ ‎(2)等差中项法：2an＋1＝an＋an＋2(n∈N*)⇔{an}是等差数列。‎ ‎(3)通项公式：an＝pn＋q(p，q为常数)⇔{an}是等差数列。‎ ‎(4)前n项和公式：Sn＝An2＋Bn(A，B为常数)⇔{an}是等差数列。‎ ‎【变式训练】　已知数列{an}的各项均为正数，前n项和为Sn，且Sn＝(n∈N*)。‎ ‎(1)求证：数列{an}是等差数列；‎ ‎(2)设bn＝，Tn＝b1＋b2＋…＋bn，求Tn。‎ ‎【解析】　(1)证明：Sn＝(n∈N*)，①‎ Sn－1＝(n≥2)。②‎ ‎①－②得an＝(n≥2)，‎ 整理得(an＋an－1)(an－an－1)＝an＋an－1(n≥2)。‎ ‎∵数列{an}的各项均为正数，‎ ‎∴an＋an－1≠0，∴an－an－1＝1(n≥2)。‎ 当n＝1时，a1＝1，∴数列{an}是首项为1、公差为1的等差数列。‎ ‎(2)由(1)得Sn＝，‎ ‎∴bn＝＝＝2，‎ ‎∴Tn＝2＋＋＋…＋＝2＝。‎ ‎【答案】　(1)见解析　(2)Tn＝ 考点三 ‎ 等差数列的性质及应用 ‎【典例3】　(1)(2015·全国卷Ⅱ)设Sn是等差数列{an}的前n项和，若a1＋a3＋a5＝3，则S5＝(　　)‎ A．5　　　 B．‎7　‎　　‎ C．9　　　 D．11‎ ‎(2)设等差数列{an}的前n项和为Sn，且S3＝－12，S9＝45，则S12＝________。‎ ‎(3)已知{an}，{bn}都是等差数列，若a1＋b10＝9，a3＋b8＝15，则a5＋b6＝________。‎ ‎【解析】　(1)解法一：∵a1＋a5＝‎2a3，∴a1＋a3＋a5＝‎3a3＝3，∴a3＝1，∴S5＝＝‎5a3＝5。故选A。‎ 解法二：∵a1＋a3＋a5＝a1＋(a1＋2d)＋(a1＋4d)＝‎3a1＋6d＝3，‎ ‎∴a1＋2d＝1，‎ ‎∴S5＝‎5a1＋d＝5(a1＋2d)＝5。故选A。‎ ‎(2)因为{an}是等差数列，所以S3，S6－S3，S9－S6，S12－S9成等差数列，所以2(S6－S3)＝S3＋(S9－S6)，即2(S6＋12)＝－12＋(45－S6)，解得S6＝3；又2(S9－S6)＝(S6－S3)＋(S12－S9)，即2×(45－3)＝(3＋12)＋(S12－45)，解得S12＝114。‎ ‎(3)因为{an}，{bn}都是等差数列，所以‎2a3＝a1＋a5,2b8＝b10＋b6，所以2(a3＋b8)＝(a1＋b10)＋(a5＋b6)，即2×15＝9＋(a5＋b6)，解得a5＋b6＝21。‎ ‎【答案】　(1)A　(2)114　(3)21‎ 反思归纳　在等差数列{an}中，数列Sm，S‎2m－Sm，S‎3m－S‎2m也成等差数列；也是等差数列。等差数列的性质是解题的重要工具。‎ ‎【变式训练】　(1)(2016·银川模拟)已知{an}是等差数列，a4＝15，S5＝55，则过点P(3，a3)，Q(4，a4)的直线斜率为(　　)‎ A．－4　　　 B.　　　‎ C．4　　　 D．－ ‎(2)已知等差数列{an}的公差为2，项数是偶数，所有奇数项之和为15，所有偶数项之和为25，则这个数列的项数为(　　)‎ A．10 B．20 ‎ C．30 D．40‎ ‎【解析】　(1)∵S5＝‎5a3＝55，∴a3＝11，∴k＝＝＝4。故选C。‎ ‎(2)设这个数列有2n项，则由等差数列的性质可知：偶数项之和减去奇数项之和等于nd，即25－15＝2n，故2n＝10，即数列的项数为10。故选A。‎ ‎【答案】　(1)C　(2)A 考点四 ‎ 等差数列前n项和的最值问题…………母题发散 ‎【典例4】　在等差数列{an}中，已知a1＝20，前n项和为Sn，且S10＝S15，求当n取何值时，Sn取得最大值，并求出它的最大值。‎ ‎【解析】　∵a1＝20，S10＝S15，‎ ‎∴10×20＋d＝15×20＋d，‎ ‎∴d＝－。‎ 解法一：由an＝20＋(n－1)×＝－n＋。‎ 得a13＝0。‎ 即当n≤12时，an>0，当n≥14时，an<0。‎ ‎∴当n＝12或13时，Sn取得最大值，‎ 且最大值为S12＝S13＝12×20＋×＝130。‎ 解法二：Sn＝20n＋· ‎＝－n2＋n ‎＝－2＋。‎ ‎∵n∈N*，∴当n＝12或13时，Sn取得最大值，且最大值为S12＝S13＝130。‎ 解法三：由S10＝S15得a11＋a12＋a13＋a14＋a15＝0。‎ ‎∴‎5a13＝0，即a13＝0。‎ ‎∴当n＝12或13时，Sn取得最大值，且最大值为S12＝S13＝130。‎ ‎【答案】　当n＝12或13时，Sn取得最大值，且最大值为S12＝S13＝130‎ ‎【母题变式】　若将本典例条件“a1＝‎20”‎改为“a1＝－‎20”‎，其他条件不变，求当n取何值时，Sn取得最小值，并求出最小值。‎ ‎【解析】　由S10＝S15，得a11＋a12＋a13＋a14＋a15＝0，‎ ‎∴a13＝0。又a1＝－20，∴a12<0，a14>0，‎ ‎∴当n＝12或13时，Sn取得最小值，‎ 最小值S12＝S13＝＝－130。‎ ‎【答案】　当n＝12或13时，Sn取得最小值，‎ 最小值S12＝S13＝－130。‎ ‎【拓展变式】　设Sn为等差数列{an}的前n项和，(n＋1)Sn0，a7<0，即数列{an}前7项均小于0，第8项大于零，所以Sn的最小值为S7。故选D。‎ ‎【答案】　D 微考场　新提升 ‎1．已知数列{an}为等差数列，其前n项和为Sn，若a3＝6，S3＝12，则公差d等于(　　)‎ A．1　　　 B.　　　‎ C．2　　　 D．3‎ 解析　由已知得S3＝‎3a2＝12，即a2＝4，∴d＝a3－a2＝6－4＝2。故选C。‎ 答案　C ‎2．(2016·长春二模)已知等差数列{an}的前n项和为Sn，满足a2 016＝S2 016＝2 016，则a1等于(　　)‎ A．－2 017 B．－2 016‎ C．－2 015 D．－2 014‎ 解析　S2 016＝＝1 008(a1＋a2 016)＝2 016，∴a1＋a2 016＝2。又∵a2 016＝2 016，∴a1＝－2 014。故选D。‎ 答案　D ‎3．(2016·临沂质检)在等差数列{an}中，若a2＋a4＋a6＋a8＋a10＝80，则a7－a8的值为(　　)‎ A．4 B．6 ‎ C．8 D．10‎ 解析　∵a2＋a4＋a6＋a8＋a10＝‎5a6＝80，∴a6＝16。∴a7－a8＝＝＝8。‎ 答案　C ‎4．已知在数列{an}中，a3＝2，a5＝1，若是等差数列，则a11等于________。‎ 解析　记bn＝，则b3＝，b5＝，数列{bn}的公差为×＝，b1＝，∴bn＝，即＝。∴an＝，故a11＝0。‎ 答案　0‎ ‎5．已知An＝{x|2n