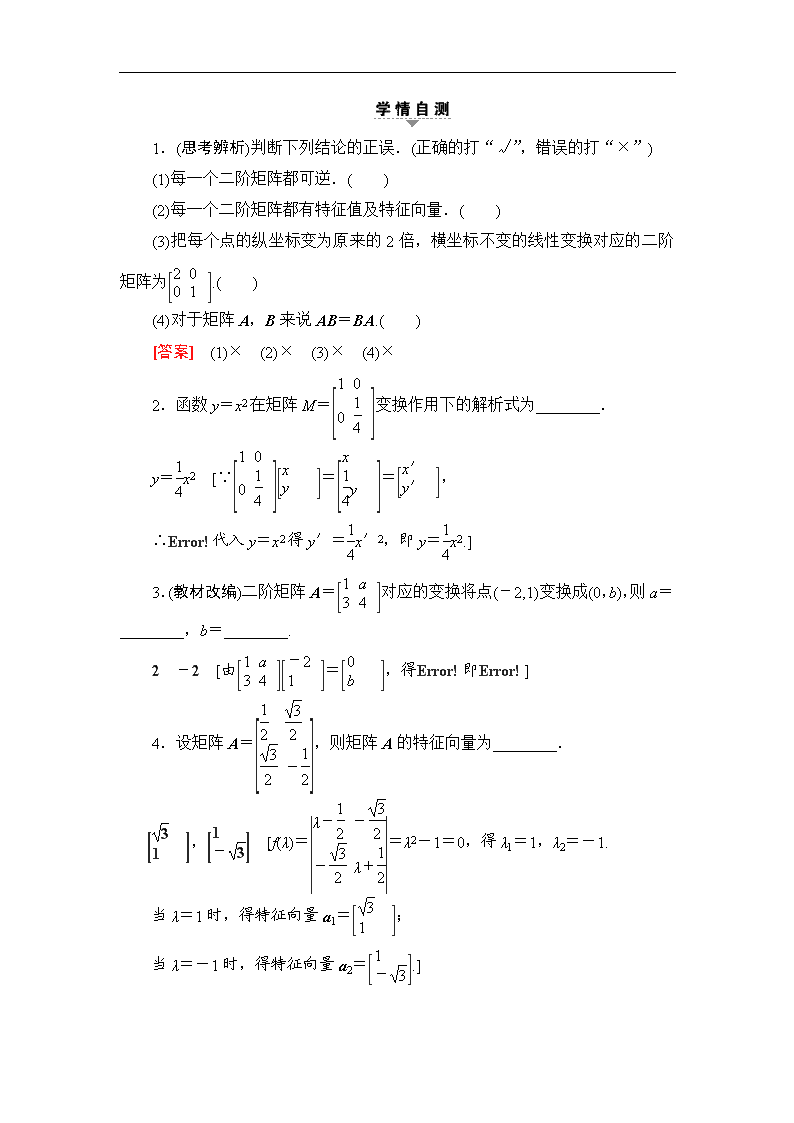高考数学复习 17-18版 附加题部分 第5章 第71课 矩阵与变换 12页

第五章　矩阵与变换 第71课 矩阵与变换 ‎[最新考纲]‎ 内容 要求 A B C 矩阵的概念 ‎√‎ 二阶矩阵与平面向量 ‎√‎ 常见的平面变换 ‎√‎ 变换的复合与矩阵的乘法 ‎√‎ 二阶逆矩阵 ‎√‎ 二阶矩阵的特征值与特征向量 ‎√‎ 二阶矩阵的简单应用 ‎√‎ ‎1．乘法规则 ‎(1)行矩阵[a11　a12]与列矩阵的乘法规则：‎ ‎[a‎11　‎a12]＝a11×b11＋a12×b21.‎ ‎(2)二阶矩阵与列向量的乘法规则：‎ ＝.‎ ‎(3)两个二阶矩阵相乘的结果仍然是一个矩阵，其乘法法则如下：‎ ‎＝.‎ ‎(4)两个二阶矩阵的乘法满足结合律，但不满足交换律和消去律．‎ 即(AB)C＝A(BC)，‎ AB≠BA，‎ 由AB＝AC不一定能推出B＝C.‎ 一般地，两个矩阵只有当前一个矩阵的列数与后一个矩阵的行数相等时才能进行乘法运算．‎ ‎2．常见的平面变换 ‎(1)恒等变换：如；‎ ‎(2)伸压变换：如；‎ ‎(3)反射变换：如；‎ ‎(4)旋转变换：如，其中θ为旋转角度；‎ ‎(5)投影变换：如，；‎ ‎(6)切变变换：如(k∈R，且k≠0)．‎ ‎3．逆变换与逆矩阵 ‎(1)对于二阶矩阵A、B，若有AB＝BA＝E，则称A是可逆的，B称为A的逆矩阵；‎ ‎(2)若二阶矩阵A、B均存在逆矩阵，则AB也存在逆矩阵，且(AB)－1＝B－1A－1.‎ ‎4．特征值与特征向量 设A是一个二阶矩阵，如果对于实数λ，存在一个非零向量α，使Aα＝λα，那么λ称为A的一个特征值，而α称为A的属于特征值λ的一个特征向量．‎ ‎5．特征多项式 设A＝是一个二阶矩阵，λ∈R，我们把行列式f(λ)＝＝λ2－(a＋d)λ＋ad－bc，称为A的特征多项式．‎ ‎1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)‎ ‎(1)每一个二阶矩阵都可逆．(　　)‎ ‎(2)每一个二阶矩阵都有特征值及特征向量．(　　)‎ ‎(3)把每个点的纵坐标变为原来的2倍，横坐标不变的线性变换对应的二阶矩阵为.(　　)‎ ‎(4)对于矩阵A，B来说AB＝BA.(　　)‎ ‎[答案]　(1)×　(2)×　(3)×　(4)×‎ ‎2．函数y＝x2在矩阵M＝变换作用下的解析式为________．‎ y＝x2　[∵＝＝，‎ ‎∴代入y＝x2得y′＝x′2，即y＝x2.]‎ ‎3．(教材改编)二阶矩阵A＝对应的变换将点(－2,1)变换成(0，b)，则a＝________，b＝________.‎ ‎2　－2　[由＝，得即]‎ ‎4．设矩阵A＝，则矩阵A的特征向量为________．‎ ，　[f(λ)＝＝λ2－1＝0，得λ1＝1，λ2＝－1.‎ 当λ＝1时，得特征向量a1＝；‎ 当λ＝－1时，得特征向量a2＝.]‎ ‎5．已知矩阵A＝，B＝，若AX＝B，则矩阵X＝________.‎ 　[设X＝，由＝，得 解得∴X＝.]‎ 二阶矩阵与线性变换 ‎　二阶矩阵M对应的变换将点(1，－1)与(－2,1)分别变成点(－1，－1)与(0，－2)．‎ ‎(1)求矩阵M；‎ ‎(2)设直线l在变换M作用下得到了直线m：x－y＝4.求直线l的方程. ‎ ‎【导学号：62172370】‎ ‎[解]　(1)设二阶矩阵M＝.‎ 依题意＝，＝，‎ 也就是＝，＝，‎ ‎∴且 解得a＝1，b＝2，c＝3，d＝4，因此所求矩阵M＝.‎ ‎(2)∵M＝，∴坐标变换公式为 ‎∵(x′，y′)是直线m：x－y＝4上的点．‎ ‎∴(x＋2y)－(3x＋4y)＝4，‎ 即x＋y＋2＝0，∴直线l的方程为x＋y＋2＝0.‎ ‎[规律方法]　1.二阶矩阵与线性变换的题目往往和矩阵的基本运算相结合命题．包括二阶矩阵的乘法，矩阵与向量的乘法等．‎ ‎2．(1)二阶矩阵与线性变换涉及变换矩阵、变换前的曲线方程、变换后的曲线方程三个要素．知其二可求第三个．(2)在解决通过矩阵进行平面曲线的变换问题时，要把变换前后的变量区别清楚，防止混淆．‎ ‎[变式训练1]　(2017·南通二调)在平面直角坐标系xOy中，设点A(－1,2)在矩阵M＝对应的变换作用下得到点A′，将点B(3,4)绕点A′逆时针旋转90°得到点B′，求点B′的坐标．‎ ‎[解]　设B′(x，y)，‎ 依题意，由＝，得A′(1,2)．‎ 则＝(2,2)，＝(x－1，y－2)．‎ 记旋转矩阵N＝，‎ 则＝，即＝，解得所以点B′的坐标为(－1,4).‎ 求逆矩阵 ‎　已知矩阵A＝.‎ ‎(1)求逆矩阵A－1；‎ ‎(2)若二阶矩阵X满足AX＝，试求矩阵X.‎ ‎[解]　(1)∵det(A)＝＝－1≠0.‎ ‎∴矩阵A是可逆的，‎ ‎∴A－1＝＝.‎ ‎(2)∵AX＝，∴A－1AX＝A－1，‎ ‎∴X＝＝.‎ ‎[规律方法]　求逆矩阵的方法：‎ ‎(1)待定系数法 设A是一个二阶可逆矩阵，AB＝BA＝E；‎ ‎(2)公式法 A＝＝ad－bc≠0，有A－1＝.‎ ‎[变式训练2]　已知矩阵A＝，B＝，求矩阵A－1B.‎ ‎[解]　设矩阵A的逆矩阵为，‎ 则＝，‎ 即＝，‎ 故a＝－1，b＝0，c＝0，d＝，‎ 从而A的逆矩阵为A－1＝，‎ 所以A－1B＝＝.‎ 特征值与特征向量 ‎　(2017·苏州模拟)求矩阵M＝的特征值和特征向量. ‎ ‎【导学号：62172371】‎ ‎[解]　特征多项式f(λ)＝＝(λ＋1)(λ－6)－8＝λ2－5λ－14＝(λ－7)(λ＋2)，由f(λ)＝0，解得λ1＝7，λ2＝－2.‎ 将λ1＝7代入特征方程组，得即y＝2x，可取为属于特征值λ1＝7的一个特征向量，‎ 同理，λ2＝－2时，特征方程组是即x＝－4y，所以可取为属于特征值λ2＝－2的一个特征向量．‎ 综上所述，矩阵M＝有两个特征值λ1＝7，λ2＝－2；‎ 属于λ1＝7的一个特征向量为，属于λ2＝－2的一个特征向量为.‎ ‎[规律方法]　已知A＝，求特征值和特征向量的步骤：‎ ‎(1)令f(λ)＝＝(λ－a)(λ－d)－bc＝0，求出特征值λ；‎ ‎(2)列方程组 ‎(3)赋值法求特征向量，一般取x＝1或者y＝1，写出相应的向量．‎ ‎[变式训练3]　(2015·江苏高考)已知x，y∈R，向量α＝是矩阵A＝的属于特征值－2的一个特征向量，求矩阵A以及它的另一个特征值．‎ ‎[解]　由已知，得Aα＝－2α，‎ 即＝＝，‎ 则即 所以矩阵A＝.‎ 从而矩阵A的特征多项式f(λ)＝(λ＋2)(λ－1)，‎ 所以矩阵A的另一个特征值为1.‎ ‎[思想与方法]‎ ‎1．二阶矩阵与平面列向量乘法：＝，这是所有变换的基础．‎ ‎2．证明两个矩阵互为逆矩阵时，切记从两个方向进行，即AB＝E＝BA.‎ ‎3．二元一次方程组相应的矩阵方程为AX＝B，其中A＝为系数矩阵，X为未知数向量，B＝为常数向量．‎ ‎4．若某一向量在矩阵交换作用下的像与原像共线，则称这个向量是属于该变换矩阵的特征向量，相应共线系数为属于该特征向量的特征值．‎ ‎[易错与防范]‎ ‎1．两个矩阵相等，不但要求元素相同，而且要求相同元素的位置也一样．‎ ‎2．对于矩阵的乘法运算不满足消去律，即由AC＝BC不一定得到A＝B.‎ ‎3．矩阵A的属于特征值λ的特征向量不唯一，其特征值λ的特征向量共线．‎ 课时分层训练(十五)‎ A组　基础达标 ‎(建议用时：30分钟)‎ ‎1．已知矩阵A＝，B＝，向量α＝，若Aα＝Bα，求实数x，y的值．‎ ‎[解]　Aα＝，Bα＝，‎ 由Aα＝Bα得解得x＝－，y＝4.‎ ‎2．(2017·如皋中学模拟)在平面直角坐标系xOy中，设点P(x,5)在矩阵M＝对应的变换下得到点Q(y－2，y)，求M－1. 【导学号：62172372】‎ ‎[解]　依题意，＝，即解得，由逆矩阵公式知，矩阵M＝的逆矩阵M－1＝，‎ 所以M－1＝＝.‎ ‎3．(2017·泰州二中月考)若点A(2,2)在矩阵M＝对应变换的作用下得到的点为B(－2,2)，求矩阵M的逆矩阵．‎ ‎[解]　由题意，得＝，‎ ‎∴ ‎∴sin α＝1，cos α＝0，‎ ‎∴M＝.‎ ‎∴＝1≠0，∴M－1＝.‎ ‎4．已知矩阵A＝，其中a∈R，若点P(1,1)在矩阵A的变换下得到点P′(0，－3)．‎ ‎(1)求实数a的值；‎ ‎(2)求矩阵A的特征值及特征向量. 【导学号：62172373】‎ ‎[解]　(1)由＝，得a＋1＝－3，∴a＝－4.‎ ‎(2)由(1)知A＝，‎ 则矩阵A的特征多项式为 f(x)＝＝(λ－1)2－4＝λ2－2λ－3，‎ 令f(λ)＝0，得矩阵A的特征值为－1或3.‎ 当λ＝－1时二元一次方程⇒y＝2x.‎ ‎∴矩阵A的属于特征值－1的一个特征向量为.‎ 当λ＝3时，二元一次方程⇒2x＋y＝0.‎ ‎∴矩阵A的属于特征值3的一个特征向量为.‎ B组　能力提升 ‎(建议用时：15分钟)‎ ‎1．(2017·苏州市期中)已知二阶矩阵M有特征值λ＝8及对应的一个特征向量e1＝，并且矩阵M将点(－1,3)变换为(0,8)．‎ ‎(1)求矩阵M；‎ ‎(2)求曲线x＋3y－2＝0在M的作用下的新曲线方程．‎ ‎[解]　(1)设M＝，由＝8及＝，‎ 得解得∴M＝.‎ ‎(2)设原曲线上任一点P(x，y)在M作用下对应点P′(x′，y′)，则＝，即解得 代入x＋3y－2＝0得x′－2y′＋4＝0，‎ 即曲线x＋3y－2＝0在M的作用下的新曲线方程为x－2y＋4＝0.‎ ‎2．(2016·南京盐城一模)设矩阵M＝的一个特征值为2，若曲线C在矩阵M变换下的方程为x2＋y2＝1，求曲线C的方程．‎ ‎[解]　由题意，矩阵M的特征多项式f(λ)＝(λ－a)(λ－1)，‎ 因矩阵M有一个特征值为2，f(2)＝0，所以a＝2.‎ 所以M＝＝＝，即 代入方程x2＋y2＝1，得(2x)2＋(2x＋y)2＝1，即曲线C的方程为8x2＋4xy＋y2＝1.‎ ‎3．(2016·苏北三市三模)已知矩阵A＝，向量α＝，计算A5α.‎ ‎[解]　因为f(λ)＝＝λ2－5λ＋6 ，由f(λ)＝0，得λ＝2或λ＝3.‎ 当λ＝2时，对应的一个特征向量为α1＝；‎ 当λ＝3时，对应的一个特征向量为α2＝.‎ 设＝m＋n，解得 所以A5α＝2×25＋1×35＝.‎ ‎4．已知矩阵A＝，B＝ ‎(1)求矩阵A的逆矩阵；‎ ‎(2)求直线x＋y－1＝0在矩阵A－1B对应的线性变换作用下所得的曲线的方程．‎ ‎[解]　(1)设A－1＝，‎ ‎∵A·A－1＝·＝，‎ ‎∴ ‎∴∴A－1＝.‎ ‎(2)A－1B＝＝，‎ 设直线x＋y－1＝0上任意一点P(x，y)在矩阵A－1B对应的线性变换作用下得P′(x′，y′)，‎ 则＝，‎ ‎∴即 代入x＋y－1＝0得x′＋3y′＋(－y′)－1＝0，‎ 可化为：x′＋2y′－1＝0，‎ 即x＋2y－1＝0为所求的曲线方程．‎