上海教育高中数学二下点到直线的距离 6页

‎11.4 点到直线的距离 ‎ 上海市控江中学 曾国光 一． 教学内容分析 ‎“点到直线的距离”是“坐标平面上的直线”一章的最后一节内容.作为直线方程和向量方法的应用，教材中，点P（x0,y0）到直线l:Ax+By+C=0的距离公式的推导经过了以下过程：（1）作出距离PQ，（2）利用向量的数量积，根据，利用Q点在直线l上，求出PQ，得到公式.‎ 在推导过程中，有两个要点：一是应用数量积的几何意义计算两点之间的距离；二是应用“若点在直线上，则点的坐标满足直线方程”进行整体代换.应用向量的方法，运算比较简捷，在此体现了向量方法的优势.‎ 然而，解析几何的核心思想，是通过用方程表示曲线，通过研究方程的解的情况反映曲线的几何性质，所以面对“如何求点P(x0,y0)到直线l:Ax+By+C=0的距离”这个问题，一个基本的解题思路是：写出直线 PQ的方程，求出直线 PQ与直线l的交点Q的坐标，最后求出|PQ|的长度.其中，解方程组，求 Q点坐标是关键，有行列式知识做铺垫，这个问题应该可以迎刃而解.‎ 教材放弃这个方法，体现了教材编写者突出向量应用的思路.但向量法显得技巧性强，需要较高的数学思维能力.在选择向量的过程中，有些问题如“为什么选择向量？用向量可以算出结果吗？”等，在教学时往往一时难以清楚回答.另外，在有行列式知识背景的前提下，解方程已经变得机械而且简单，所以放弃方程，与学生的认知基础有一定的差距.但是，作为教材，也不可能就同一个问题罗列两种解法，这是一种两难的选择.‎ 这也给教师的教学设计造成了困惑，是突出方程思想，还是突出向量思想？如何处理？如何选择？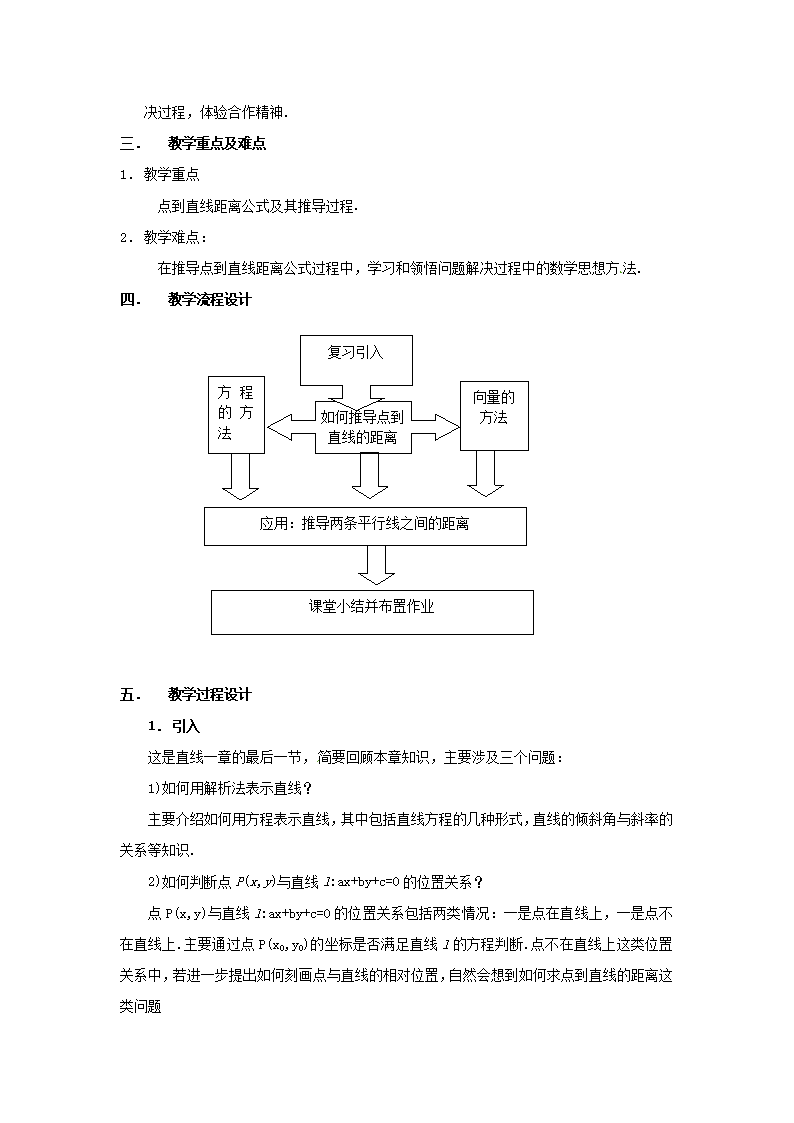才能既符合学生认知特点，又能体现新教材的特点.‎ 二． 教学目标设计 1． 通过学习，学会推导点到直线的距离公式并掌握点到直线的距离公式.‎ 2． 通过对点到直线之间公式推导方法的分析、比较与体验，领悟公式推导过程中的数学思想和思维方法，培养分析问题和解决问题的能力.‎ 3． 通过对点到直线之间的距离、平行线之间距离的探究，培养理性思维能力.经历问题解 决过程，体验合作精神.[‎ 一． 教学重点及难点 1． 教学重点 点到直线距离公式及其推导过程.‎ 2． 教学难点：‎ 在推导点到直线距离公式过程中，学习和领悟问题解决过程中的数学思想方法.‎ 二． 教学流程设计 复习引入 向量的方法 如何推导点到直线的距离 方程的方法 课堂小结并布置作业 应用：推导两条平行线之间的距离 三． 教学过程设计 ‎ 1． 引入 这是直线一章的最后一节，简要回顾本章知识，主要涉及三个问题：‎ ‎1)如何用解析法表示直线？‎ 主要介绍如何用方程表示直线，其中包括直线方程的几种形式，直线的倾斜角与斜率的关系等知识.‎ ‎2)如何判断点P(x,y)与直线l:ax+by+c=0的位置关系？‎ 点P(x,y)与直线l:ax+by+c=0的位置关系包括两类情况：一是点在直线上，一是点不在直线上.主要通过点P(x0,y0)的坐标是否满足直线l的方程判断.点不在直线上这类位置关系中，若进一步提出如何刻画点与直线的相对位置，自然会想到如何求点到直线的距离这类问题 ‎3)如何判断直线与直线的位置关系？‎ 两条直线的位置关系包括三种情况：相交、平行与重合.在直线与直线相交关系中可以进一步研究两条直线的夹角问题，包括特殊情况：垂直关系；在两条直线平行时会联想到如何求平行线间的距离，进而转化为求点到直线间的距离问题.‎ 所以，进一步讨论点到直线的距离是理性思维的结果，是完善知识体系得需要.‎ 引入中，从学生原有的知识基础出发，通过知识的逻辑结构说明为什么学习点到直线的距离，激发学生学习的兴趣，强调理性精神 1． 点到直线距离公式的推导 P Q l x y O ‎1）明确并提出问题 已知直线l：ax+by+c=0，直线外一点P(x0,y0).其中a、b、c、x0、y0为常数.如何表示点P到直线l的距离d?‎ 在解决该问题前可以作如下铺垫：‎ 可以先回顾“什么是点到直线的距离？”从几何角度作出距离，并指出点到直线距离其实是点到直线上任意一点距离的最小值.再指出点P到直线的距离是一个确定的值，它可以用x0、y0、a、b、c表示.‎ ‎2） 推导点到直线的距离公式 通过对问题的分析，归结为“如何计算线段|PQ|的长度？”.因为推导公式的方法有许多种，所以可以充分发挥学生的主观能动性，通过有效组织，引导学生积极思维，寻找问题的解决方法.‎ 主要可能有以下几类方法.‎ ‎（1）计算Q点坐标.‎ 有下列两种方法：‎ （i） 利用数量积，计算Q点坐标.具体思路：设Q（x１,y１），由与直线的一个方向向量垂直及两个条件联立方程组，解得x１,y１即可.‎ （ii） 联立方程组，计算两条直线交点Q的坐标.具体思路：写出直线PQ的方程，联立PQ与l的方程，求解Q点坐标(x1,y1).‎ ‎（2）利用向量的数量积.‎ 因为数量积可以求向量投影的长度，，所以，其中M是直线l上某一点.特别的，，可以归结为教材提供的方法.‎ ‎（3）其他方法[‎ 学生还可能想到：利用三角比，利用三角形面积，勾股定理等平面几何知识，利用函数思想求点P到直线上任意一点距离的最小值等.‎ 虽然方法有许多种，但是因为解析几何的核心思想是利用方程研究曲线，所以联立方程组是基本方法；又因为向量在解析几何是一个重要的知识和方法，对学生将来进一步学习空间解析几何有帮助，所以可以选择联立方程组计算点Q坐标与利用数量积计算|PQ|长度这两种方法具体讲解.‎ ‎ 以下为两种方法解题过程：‎ l 联立方程组，利用行列式知识求解：‎ ‎，‎ 的方程可以写成：，‎ 所以解方程组：，‎ 得；；.‎ 所以 所以. ‎ l 利用向量的数量积直接求出|PQ|的长度：‎ 由直线方程，知l的法向量为=（a,b），设M(x/，y/)是直线l上的一点，‎ 得， ‎ 因为，所以.‎ 又点M在直线l上，所以ax/+by/+c=0，即ax/+by/= -c.得.‎ 对上述两种方法进行回顾总结，并给出结论：点P(x0,y0)到直线l:ax+by+c=0的距离.‎ 在上述两种解题方法中，都需要强调一种整体代换的思想.‎ 1． 公式的应用 回到本节课开头的问题：如何推导两条平行线之间的距离公式. om]‎ 若直线l1:ax+by+c1=0,l2:ax+by+c2=0,其中a,b,c1,c2为常数且c1≠c2.如何求直线l1与l2之间的距离？ ‎ 这个问题可由学生独立完成，教师引导并主要介绍两个方法：:‎ ‎（１）将平行线之间的距离转化为求点到直线间的距离，利用刚刚推导的点到直线距离公式.‎ 在直线l上取点，则，又，所以，所以 ‎（２）利用向量数量积，直接计算 设，得，由 ‎，‎ 又，所以.‎ 2． 小结与作业 ‎1)小结 这节课主要研究三个问题：(1) 为什么要学习点到直线之间的距离？（2）点到直线之间的距离如何推导；（3）如何求平行线之间的距离.‎ 主要知识有点到直线之间距离公式及其推导方法与过程，平行线之间的距离公式及其推导方法与过程.强调了方程的方法与向量的思想.[‎ ‎2)作业：‎ 练习11.4，1、2、3；习题11.4，1、3、4、5、6‎ 一． 教学设计说明 ‎ 1． 从知识的角度讲，本节课并没有新的概念，完全是利用已经掌握的知识解决问题，获得新的结论、新的知识.所以这节课一定意义上是问题解决式教学.‎ 2． 因为问题解决的方法比较多，每种方法都面面俱到，这是不可能的，也是不现实的.如何选择成了教学的关键，这里我们从解析几何的核心思想与向量方法的重要程度考虑，选择这两种方法作为重点讲解的方法，同时也是对所学行列式知识与向量知识的一个很好的应用.在两种方法的讲解过程中，要重点引导学生体会整体代换的思想.‎ 3． 在教学的组织形式上，考虑到方法的多样性和学生思维的积极性与创造性，可以考虑充分发挥学生的主观能动性，由学生讨论并寻找问题解决方法.在寻找方法过程中，可以要求学生只谈想法，不必算出结果，但要讲清方法的来龙去脉以及解题计划，是如何想到这个方法的？用这个方法可以算到结果吗？在应用所给方法过程中可能会遇到什么问题.具体解题过程，可以根据这些解题设想由学生课后完成.‎ 4． 平行线之间距离公式的推导是对点到直线距离公式学习效果的巩固，既应用了公式，又可以利用向量的数量积.但考虑到教学时间和学生接受程度，平行线之间的距离公式可以作为思考题，留作学生课后思考，为下一节课作准备.‎