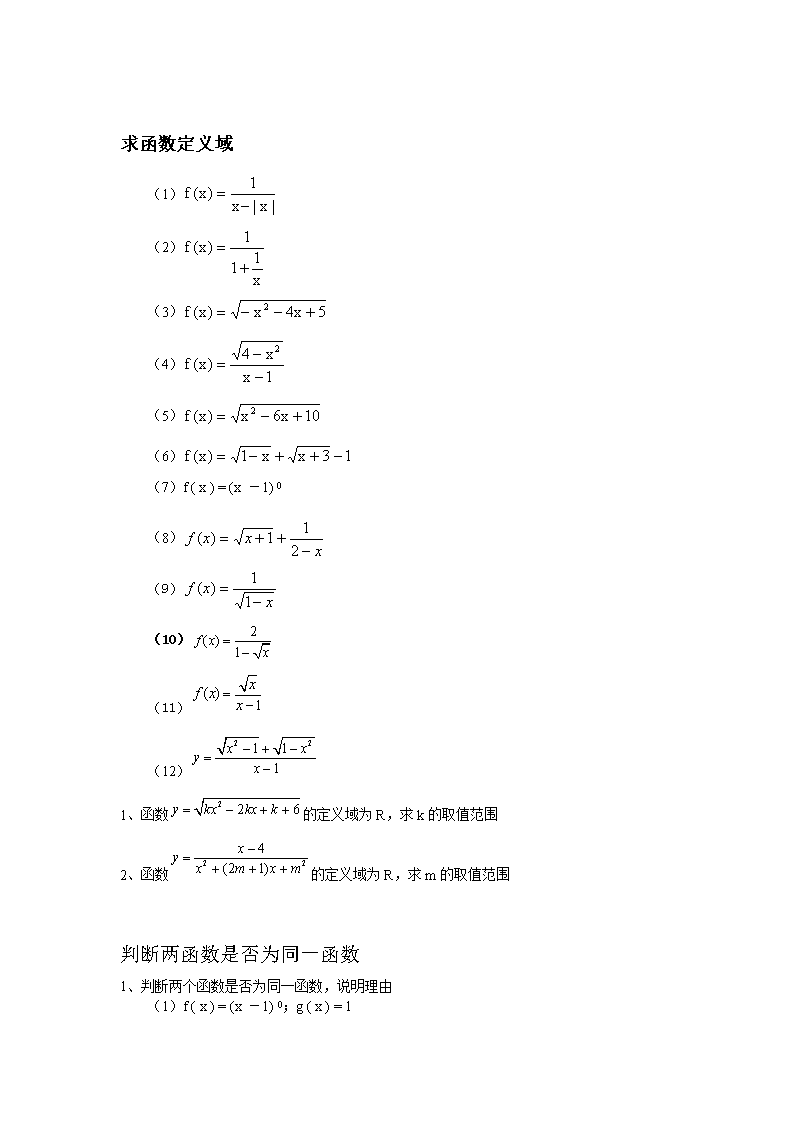高中数学必修1函数题型分析(精心整理版) 18页

2.1 函数的概念 （一）函数的概念 设 A、B 是非空的数集，如果按照某个确定的对应关系 f，使对于集合 A 中的任意一个 数 x，在集合 B 中都有唯一确定的数 f(x)和它对应，那么就称 f：A→B 为从集合 A 到集合 B 的一个函数． 记作： y=f(x)，x∈A．（y 就是 x 在 f 作用下的对应值） 其中，x 叫做自变量，x 的取值范围 A 叫做函数的定义域；与 x 的值相对应的 y 值叫做 函数值，函数值的集合{f(x)| x∈A }叫做函数的值域． （二）构成函数的三要素： 定义域、对应关系和值域 判断两变量之间是否是函数关系 （1）定义域与对应关系是否给出， （2）根据给出的对应法则，自变量 x 在其定义域中的每一个值，是否都能确定唯一的 函数值。 （三）区间的概念 （1）区间的分类：开区间、闭区间、半开半闭区间；（a，b 为端点） 满足 a x b  的全体实数 x 的集合叫做闭区间，记作 ,a b 满足 a x b  的全体实数 x 的集合叫做开区间，记作 ,a b 满足 a x b  或 a x b  的全体实数 x 的集合叫做半开半闭区间，分别记作 [ , )a b 或 ( , ]a b （2）无穷区间； （3）区间的数轴表示． 函数概念 1、如下图可作为函数 )(xf 的图像的是( ) A B C D 2. 下列四个图形中，不是．．以 x 为自变量的函数的图象是 x y O x y O x y O x y O A. B. C. D. 求函数定义域 （1） |x|x 1)x(f  （2） x 11 1)x(f   （3） 5x4x)x(f 2  （4） 1x x4)x(f 2   （5） 10x6x)x(f 2  （6） 13xx1)x(f  （7）f ( x ) = (x －1) 0 （8） xxxf  2 11)( （9） x xf   1 1)( （10） 2( ) 1 f x x   （11） ( ) 1 xf x x   （12） 2 21 1 1 x xy x     1、函数 2 2 6y kx kx k    的定义域为 R，求 k 的取值范围 2、函数 2 2 4 (2 1) xy x m x m     的定义域为 R，求 m 的取值范围 判断两函数是否为同一函数 1、判断两个函数是否为同一函数，说明理由 （1）f ( x ) = (x －1) 0；g ( x ) = 1 （2）f ( x ) = x； g ( x ) = 2x （3）f ( x ) = x 2；f ( x ) = (x + 1) 2 （4）f ( x ) = | x | ；g ( x ) = 2x 2、判断两个函数是否为同一函数，说明理由 （1） ( 3)( 5) 3 x xy x    ； 5y x  （2） 1 1y x x   ； ( 1)( 1)y x x   （3） 3 4 3y x x  ； 3 1y x x  （4） 11y x   ； 11u v   求函数解析式 （1）代入法 1、 已知函数 2( ) 1f x x  ,求 ( )f x ， (1 )f x 2、 已知函数 )31(12)(  xxxf ，则 （ ） A． )1( xf = )20(22  xx B． )1( xf = )42(12  xx C． )1( xf = )20(22  xx D． )1( xf = )42(12  xx 3、 已知 2( )f x x m  ， ( ) ( ( ))g x f f x ，求 ( )g x 的解析式。 （2）换元法 1、已知 2( 1)f xx   ，求 ( )f x ； 2、已知函数 2( 1)f x x  ，求 ( )f x 3、 若 1( ) 1 xf x x   ,求 ( ).f x 4、若 ( 1) 2f x x x   ,求 ( ).f x 5. 已知ƒ( x +1)=x+1，则函数ƒ(x)的解析式为 A.ƒ(x)=x2 B.ƒ(x)=x2+1 C.ƒ(x)=x2-2x+2 D.ƒ(x)=x2-2x 6．已知 2)1( xxf  ，则 ( )f x 的表达式为 （ ） A． 2( ) 2 1f x x x   B． 2( ) 2 1f x x x   C． 2( ) 2 1f x x x   D． 2( ) 2 1f x x x   9、设函数 ( ) 2 1f x x  ，则方程 (2 1)f x x  的解为 7. 已知 )0(1)21( 2 2  x x xxf ，则 )2 1(f 的值为____________________。 8．已知 f(2x－1)＝x2，则 f(5)＝______．9 （3）待定系数法 1、若 )(xf 是一次函数， 14)]([  xxff 且，则 )(xf = _________________. 2、已知 ( )f x 是一次函数，且满足 3 ( 1) 2 ( 1) 2 17f x f x x     ，求 ( )f x ； 分段函数 函数图像 1. 已知函数解析法可表示为     , 0,1 2 , 1,2 x x y x x      ，用图像表示这个函数。 2. 把下列函数分区间表示，并作出函数的图像 （1） 1 | |y x  （2） 3 | |y x  （3） | 1| | 4 |y x x    （4） 2 2 2 (0 3)( ) 6 ( 2 0) x x xf x x x x          （5）     ，＜ ，＋ )2(2 )2(22 xx xx （6） 2 2 ( 1) ( ) ( 1 2) 2 ( 2) x x f x x x x x        ≤ ≥ （7）       2( 1) , , 1 2 2, 1,1 1 1, 1, x x y x x xx                求函数值 1. 作函数 2 , 1 0 ,0 1 ,1 2 x x y x x x x           的图像，并求 1 1( 0.8), ( ), ( )2 3f f f 2、设函数 3,( 10)( ) ( ( 5)),( 10) x xf x f f x x      ，则 (5)f ＝_____ 3、已知函数      3, 10, , 85 , 10, x x f x x N ff f x x          其中 则 （ ） Ａ．２ Ｂ．４ Ｃ．６ Ｄ．７ 4、已知       1, 1 3, 1 x xf x x x      ，那么 1 2f f        的值是 （ B ） A. 2 5 B. 2 3 C. 2 9 D. 2 1 5.已知 f（x）=       )0x(0 )0x( )0x(1x ，则 f [f（－2）]＝________________. 6、已知，则      2 , 0, , 0, 3 0, 0. x x f x x f f f x           那么 的值等于 （ ） Ａ．０ Ｂ． Ｃ． 2x Ｄ．９ 7. 定义在 R 上的函数 ( )f x 满足 12 , 0,( ) ( 1) ( 2), 0. x xf x f x f x x        则 ( 1)f   ______， (33)f  ______． 4 2 给出函数值求自变量的值 1、设函数 f（x）＝     ，＜ ，＋ )2(2 )2(22 xx xx 则 f（－4）＝____，又知 f（ 0x ）＝8，则 0x ＝____ 2、设 2 2 ( 1) ( ) ( 1 2) 2 ( 2) x x f x x x x x        ≤ ≥ ，若 ( ) 3f x  ，则 x=____________。 3、函数 y=       1)( 5- 1),(0 3 0),( 32 xx xx xx 的最大值是_______. 4. 已知      2 1 )( x x xf  ),0( ),0( ),0(    x x x 如果 3)( 0 xf ，那么 0x ____________。 5．已知函数    x xxf 4 )( 2 )1( )1(   x x 若 9)( xf ，则 x = . 6 、 设 函 数 2( 1) .( 1)( ) 4 1.( 1) x xf x x x        ， 则 使 得 ( ) 1f x  的 自 变 量 x 的 取 值 范 围 是 __________； 7、 已知 1 ( 0)( ) 1 ( 0) xf x x    　　 　　 ，则不等式 ( 2) ( 2) 5x x f x    的解集是________ 8、 已知      0,1 0,1)( x xxf ，则不等式 4)2()12(  xfxx 的解集是 【-5，1】 函数单调性 单调性概念考察 1. 若函数 )(xf 在区间（a，b）上为增函数，在区间（b，c）上也是增函数，则函数 )(xf 在 区间（a，c）上（ ） （A）必是增函数 （B）必是减函数 （C）是增函数或是减函数（D）无法确定增减性 2．函数 )(xf 在 ),( ba 和 ),( dc 都是增函数，若 ),(),,( 21 dcxbax  ，且 21 xx  那么（ ） A． )()( 21 xfxf  B． )()( 21 xfxf  C． )()( 21 xfxf  D．无法确定 3．已知函数 y＝f(x)在 R 上是增函数，且 f(2m＋1)＞f(3m－4)，则 m 的取值范围是( ) A．(－∞，5) B．(5，＋∞) C． ),5 3(  D． )5 3,( 4 ． 函 数 ( )f x 的 定 义 域 为 ),( ba ， 且 对 其 内 任 意 实 数 1 2,x x 均 有 ： 1 2 1 2( )[ ( ) ( )] 0x x f x f x   ，则 ( )f x 在 ),( ba 上是( ) （A）增函数 （B）减函数 （C）奇函数 （D）偶函数 5. 函数 f(x)在(0，＋∞)上为减函数，那么 f(a2－a＋1)与 )4 3(f 的大小关系是______。 6．已知函数 f(x)在区间[a，b]上单调，且 f(a)f(b)＜0，则方程 f(x)=0 在区间[a，b]内（ ） A．至少有一实根 B．至多有一实根 C．没有实根 D．必有唯一的实根 7．当 时，函数 的值有正也有负，则实数 a 的取值范围是 （） A． B． C． D． 8. 已知函数 f(x)在其定义域 D 上是单调函数，其值域为 M，则下列说法中 ①若 x0∈D，则有唯一的 f(x0)∈M ②若 f(x0)∈M，则有唯一的 x0∈D ③对任意实数 a，至少存在一个 x0∈D，使得 f(x0)＝a ④对任意实数 a，至多存在一个 x0∈D，使得 f(x0)＝a 错误的个数是( ) A．1 个 B．2 个 C．3 个 D．4 个 9．已知f(x)在区间(－∞，＋∞)上是增函数，a、b∈R 且a＋b≤0，则下列不等式中正确的是（ ） A．f(a)＋f(b)≤－f(a)＋f(b)］ B．f(a)＋f(b)≤f(－a)＋f(－b) C．f(a)＋f(b)≥－f(a)＋f(b)］ D．f(a)＋f(b)≥f(－a)＋f(－b) 10．已知 f(x)是定义在(－2，2)上的减函数，并且 f(m－1)－f(1－2m)＞0，求实数 m 的取值 范围． 解析： ∵f(x)在(－2，2)上是减函数 ∴由 f(m－1)－f(1－2m)＞0，得 f(m－1)＞f(1－2m) ∴                  3 2 2 3 2 1 31 211 ,2212 212 m m m mm m m 即 解得 3 2 2 1  m ，∴m 的取值范围是(－ 3 2,2 1 ) 11. 已知：f(x)是定义在[－1，1]上的增函数，且 f(x－1)f(1)，则 f(x)在 R 上不是减函数； C.定义在 R 上的函数 f(x)在区间 ( ,0] 上是减函数，在区间 (0, ) 上也是减函数，则 f(x)在 R 上是减函数； D.既是奇函数又是偶函数的函数有且只有一个。 3、对于定义域为 R 的任意奇函数 f(x)一定有( ) A．f(x)－f(－x)＞0 B．f(x)－f(－x)≤0 C．f(x)·f(－x)＜0 D．f(x)·f(－x)≤0 4、 )(xf 是定义在 R 上的奇函数，下列结论中，不正确的是( ) （A） 0)()(  xfxf （B） )(2)()( xfxfxf  （C） )(xf · )( xf  ≤ 0 （D） 1)( )( xf xf 判断函数奇偶性 1．下列函数中： ①y＝x2(x∈[－1，1])； ②y＝｜x｜； ;1)( xxxf ③ ④y＝x3(x∈R)， 奇函数的个数是( ) A．1 个 B．2 个 C．3 个 D．4 个 2. 下列函数中是偶函数的是（ ） A、y=x4 (x<0) B、y=|x+1| C、y= 2 x2+1 D、y=3x-1 3．判断下列函数的奇偶性： (1) xxxf  11)( (2) 22 11)( xxxf  （3） xxy 2112  （4）        )0(2 )0(0 )0(2 2 2 xx x xx y （5） 2 | 4 | 4 9 xy x    （6）      )0(1 )0(1)( xx xxxf （7） 1 22)( 2   x xxxf ； （8） axf )( （ Rx ） （9）      )1( )1()( xx xxxf .0 ,0   x x （10） 2 2( ) 3 3f x x x    （11） 1+xf(x)=(x-1) 1-x （12） 2 2 x ( 0)f(x)= x ( 0) x x x x      （13） | 1| | 1|y x x    4、若 f(x)是偶函数，则    ) 21 1()21( ff ______． 5、下列给出的函数中，既不是奇函数也不是偶函数的是 （A） 2 xy  （B） 2y x x  （C） 2y x （D） 3y x 6.已知函数 ( 1)( )( ) x x bf x x   的图象关于原点对称，则 b  ________________．-1 奇偶函数四则运算性质 1、判断下列函数的奇偶性 (1) 2 4 13)( xxxf  (2) xxy 13  （3） xxy  4 （4） xxxf 2)( 3  ； （5） 2 | | 1y x x   （6） 1 | |y x x  2、函数 pxxxy  || ， Rx  是 （ ） A．偶函数 B．奇函数 C．不具有奇偶函数 D．与 p 有关 3．已知函数 2( ) 1f x x bx   是 R 上的偶函数，则实数b  _____；不等式 ( 1)f x x  的 解集为_____． 0 ，{ |1 2}x x  ； 4、若 3)3()2()( 2  xkxkxf 是偶函数，讨论函数 )(xf 的单调区间？ 5、已知函数 )0()( 23  acxbxaxxf 是偶函数，判 cxbxaxxg  23)( 的奇偶性。 6、已知函数 3x)1m(x)2m()x(f 2  是偶函数，求该函数的最大值并写出它的单 调递增区间。 7、若函数 2( ) ( 1) 3f x kx k x    是偶函数，则 ( )f x 的递减区间是 8、若函数 ( 1)( )y x x a   为偶函数，则 a= 2 利用函数奇偶性求解函数解析式 1、设 f(x)是 R 上的奇函数，且当 x∈[0，＋∞)时，f(x)＝x(1＋x3)，那么当 x∈(－∞，0]时， f(x)＝______． 2、已知 f（x）的定义域为 R，当 (0, )x  时， ( ) (1 2 )xf x x  ，若 f（x）为奇（偶） 函数，求 f（x）的解析式 3 、 函 数 )(xf 在 R 上 为 奇 函 数 ， 且 0,1)(  xxxf ， 则 当 0x ， )(xf . 4、已知函数 f(x)是奇函数，当 x>0 时，f(x)=x(1+x);当 x<0 时，f(x)=( ) A、-x(1-x) B、x(1-x) C、-x(1+x) D、x(1+x) 5、 已知函数  f x 是偶函数，且 0x  时，   1 .1 xf x x   ．求 (1)  5f 的值，(2)   0f x  时 x 的值；(3)当 x >0 时，  f x 的解析式 部分函数奇偶性解题 1、已知 8)( 32005  x baxxxf ， 10)2( f ，求 )2(f . 2、已知函数 f(x)=x7+ax5+bx-5，若 f(-100)=8,那么 f(100)=( ) A、-18 B、-20 C、-8 D、8 3、已知 f(x)＝x5＋ax3＋bx－8，且 f(－2)＝10，则 f(2)＝_______． 4、设函数 3( ) 2 1f x ax bx   ，且 ( 1) 3f   ，则 (1)f  ______ 题型六、函数单调性与奇偶性考察 1、设奇函数 f(x)在区间[3，7]上是增函数，且 f(3)=5,则 f(x)在区间[―7，―3]上应有最___ 值为_________ 2、已知  f x 是定义 ,  上的奇函数，且  f x 在 0, 上是减函数．下列关系式 中正确的是 ( ) Ａ．    5 5f f  Ｂ．    4 3f f Ｃ．    2 2f f  Ｄ．    8 8f f  3、 设偶函数 f(x)的定义域为 R，当 x ],0[  时 f(x)是增函数，则 f(-2),f( ),f(-3)的大小关 系是（ ） （A）f( )>f(-3)>f(-2) （B）f( )>f(-2)>f(-3) （C）f( )f(5) B、f(3)f(3) D、f(-2)>f(1) 7、设函数 ( )f x 是 R 上的偶函数，且在 ( ,0) 上是减函数，若 ( ) (1)f a f ，则实数 a 的取 值范围 8、已知奇函数 )(xf 是定义在 )2,2( 上的减函数,若 0)12()1(  mfmf ，求实 数 m 的取值范围为 。 9、定义在[-1，1]上的减函数 y=f(x)是奇函数。若 f(a2-a-1)+f(4a-5)>0,求实数 a 的取值范围 10、设 f(x)是定义在 R 上的偶函数，且在(－∞，0)上是增函数，则 f(－2)与 f(a2－2a＋3)(a ∈R)的大小关系是______． 11、下列命题中， ①函数 xy 1 是奇函数，且在其定义域内为减函数； ②函数 y＝3x(x－1)0 是奇函数，且在其定义域内为增函数； ③函数 y＝x2 是偶函数，且在(－3，0)上为减函数； ④函数 y＝ax2＋c(ac≠0)是偶函数，且在(0，2)上为增函数； 真命题是______． 12、已知函数 f(x)为偶函数，在（0,+ ) 上为减函数，若 f( )2 1 ﹥0﹥f( 3 )，则方 程 f(x)＝0 的根的个数是 （ ） A 2 B 2 或 1 C 3 D 2 或 3 13、定义在 R 上的偶函数 )(xf 在 )0,( 是单调递减，若 )2()6( afaf  ，则 a 的取值 范围是如何？ 14、 设奇函数 f(x)的定义域为[-5,5].若当 x∈[0,5]时, f(x) 的 图 象 如 右 图 , 则 不 等 式   0xf 的 解 是 . 15、设奇函数  f x 在  0, 上为增函数，且  2 0f  ，则不等式     0f x f x x    的解 集为（ ） A．    2,0 2,  B．   , 2 0,2   C．    , 2 2,   D．   2,0 0,2  16、已知偶函数 ( )f x 在 (0, ) 上为减函数， 且 (2) 0f  ，则不等式 ( ) ( ) 0f x f x x    的解集 为 ．   - -2 0 2 ， ， 。 17.奇函数 f(x)在 ( ,0) 上单调递增，若 f(-1)=0,则不等式 f(x)<0 的解集是( ) A. ( , 1) (0,1)   B. ( , 1) (1, )   C. ( 1,0) (0,1)  D. ( 1,0) (1, )  18、设 f(x)是奇函数，且在区间（0，+∞）上是增函数，又 f(－2)=0,求不等式 f(x－1)<0 的 解集。 19、已知 ( )y f x 是偶函数且图像与 x轴有四个交点，则方程 ( ) 0f x  的所有实根之和= 20、已知 ( )f x 定义在 R 上，对任意 ,x y R ，有 ( ) ( ) 2 ( ) ( )f x y f x y f x f y     ，且 (0) 0f  （1）求证： (0) 1f  （2）求证： ( )y f x 是偶函数 21、已知函数 ( )f x ， x R ，若对任意实数 ,a b ，都有 ( ) ( ) ( )f a f b f a b   ，求证： ( )f x 为奇函数。 22、已知函数 ( )f x 是奇函数， ( )g x 是偶函数且 2( ) ( ) 2g x f x x x    ，求 ( )f x ， ( )g x 的 解析式 23 、 若 函 数 ( )y f x 是 定 义 在 R 上 的 奇 函 数 ， 对 任 意 ,x y R ， 恒 有 ( ) ( ) ( ), ( 3) , (12)f x y f x f y f m f     求 24、 函数 2( ) 1 ax bf x x   是定义在 ( 1,1) 上的奇函数，且 1 2( )2 5f  （1）确定函数 ( )f x 的解析式 （2）用定义法证明 ( )f x 在 ( 1,1) 上是奇函数 （3）解不等式 ( 1) ( ) 0f t f t  