高中数学第二章函数第2节对函数的进一步认识第1课时基础知识素材北师大版必修11 6页

2.1 函数概念 1．了解生活中的变量关系． 2．理解函数的概念． 3．会求出简单函数的定义域、值域． 1．生活中的变量关系 (1)依赖关系：在某变化过程中有两个变量，如果其中一个变量的值发生了变化，另一 个变量的值也会随之发生变化，那么就称这两个变量具有依赖关系．如果变量 x，y 具有依 赖关系，对于其中一个变量 x 的每一个值，另一个变量 y 都有________的值时，那么称变量 y 是变量 x 的函数，即这两个变量之间具有函数关系． (2)非依赖关系：在某变化过程中有两个变量，如果其中一个变量的值发生了变化，另 一个变量的值不受任何影响，那么就称这两个变量具有非依赖关系． 函数关系是特殊的依赖关系，具有依赖关系的两个变量有的是函数关系，有的不是函数 关系．因此说依赖关系不一定是函数关系，而函数关系是依赖关系．例如，积雪层对越冬作 物具有防冻保暖作用，大雪可以防止土壤中的热量向外散发，又可阻止外界冷空气的侵入， 具有增墒肥田作用．所以下雪与来年的丰收具有依赖关系，但不是函数关系． 【做一做 1－1】 张大爷种植了 10 亩小麦，每亩施肥 x 千克，小麦总产量为 y 千克， 则( )． A．x，y 之间有依赖关系 B．x，y 之间有函数关系 C．y 是 x 的函数 D．x 是 y 的函数 【做一做 1－2】 某人骑车的速度是 v 千米/时，他骑 t 小时，走的路程 s 是多少？路 程是时间的函数吗？ 2．函数的概念 给定两个非空____________A 和 B，如果按照某个对应关系 f，对于集合 A 中________ 数 x，在集合 B 中都存在____________确定的数 f(x)与之对应，那么就把对应关系 f 叫作定 义在集合 A 上的函数，记作 f：A→B，或 y＝______________，x∈A.此时，x 叫作自变量， 集合 A 叫作函数的定义域，集合__________叫作函数的值域．习惯上我们称 y 是 x 的函数． (1)符号 y＝f(x)表示变量 y 是变量 x 的函数，它仅仅是函数符号，并不表示 y 等于 f 与 x 的乘积；符号 f(x)与 f(m)既有区别又有联系，当 m 是变量时，函数 f(x)与函数 f(m) 是一样的；当 m 是常数时，f(m)表示自变量 x＝m 时对应的函数值，是一个常量． (2)函数的三要素：定义域、对应关系、值域．有时给出的函数没有明确说明定义域， 这时，它的定义域就是自变量的允许取值范围，此时的定义域又称为此函数的“自然定义 域”；如果函数涉及实际问题，它的定义域还需使实际问题有意义，此时的定义域又称为此 函数的“临时定义域”． 【做一做 2】 下列式子中不能表示函数 y＝f(x)的是( )． A．x＝y2＋1 B．y＝2x2＋1 C．x－2y＝6 D．x＝ y 3．区间与无穷的概念 (1)区间 设 a，b 是两个实数，而且 a＜b，规定如下表： 定义 名称 符号 几何表示 {x|a≤x≤b} 闭区间 ______ {x|a＜x＜b} 开区间 ______ {x|a≤x＜b} 左闭右 开区间 ______ {x|a＜x≤b} 左开右 闭区间 ______ 这里实数 a，b 都叫作相应区间的________________． 并不是所有的数集都能用区间表示．例如：数集 M＝{1,2,3,4}就不能用区间表示．由 此可见，区间仍是集合，是一类特殊数集的另一种符号语言． (2)无穷的概念及无穷区间 定义 R {x|x≥a} {x|x＞a} {x|x≤a} {x|x＜a} 符号 (－∞，＋∞) ________ ________ ________ ________ 无穷大“∞”是一个符号，不是一个具体的数．因此不能将[1，＋∞)写成[1，＋∞]． 【做一做 3】 将下列集合用区间表示出来，并在数轴上表示区间． (1){x|x≥1}； (2){x|x＜1 或 x≥2}； (3){x|2≤x≤8 且 x≠5}． 答案：1．(1)唯一确定 【做一做 1－1】 A 【做一做 1－2】 解：t 小时走的路程是 s＝vt. 由于时间 t 每取一个值，路程 s 有唯一确定的值与之对应，所以路程是时间的函数． 2．数集 任何一个 唯一 f(x) {f(x)|x∈A} 【做一做 2】 A A 选项中，给定一个 x(比如 x＝5)，有两个 y(y＝±2)与它对应，所 以 y 不是 x 的函数．同理可验证其他选项中 y 都是 x 的函数． 3．(1)[a，b] (a，b) [a，b) (a，b] 端点 (2)[a，＋∞) (a，＋∞) (－∞，a] (－∞，a) 【做一做 3】 解：(1)[1，＋∞)； (2)(－∞，1)∪[2，＋∞)； (3)[2,5)∪(5,8]． 数轴表示分别如图(1)(2)(3)． 如何理解函数符号 f(x)的意义？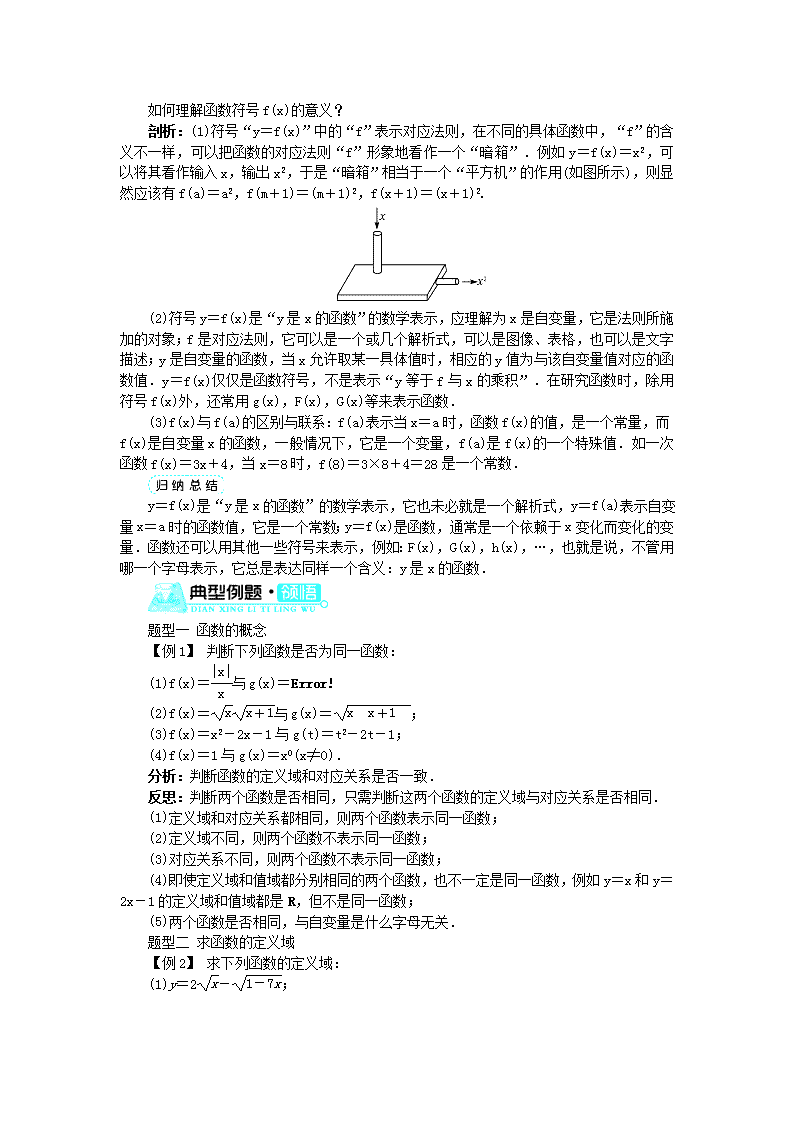 剖析：(1)符号“y＝f(x)”中的“f”表示对应法则，在不同的具体函数中，“f”的含 义不一样，可以把函数的对应法则“f”形象地看作一个“暗箱”．例如 y＝f(x)＝x2，可以 将其看作输入 x，输出 x2，于是“暗箱”相当于一个“平方机”的作用(如图所示)，则显然 应该有 f(a)＝a2，f(m＋1)＝(m＋1)2，f(x＋1)＝(x＋1)2. (2)符号 y＝f(x)是“y 是 x 的函数”的数学表示，应理解为 x 是自变量，它是法则所施 加的对象；f 是对应法则，它可以是一个或几个解析式，可以是图像、表格，也可以是文字 描述；y 是自变量的函数，当 x 允许取某一具体值时，相应的 y 值为与该自变量值对应的函 数值．y＝f(x)仅仅是函数符号，不是表示“y 等于 f 与 x 的乘积”．在研究函数时，除用 符号 f(x)外，还常用 g(x)，F(x)，G(x)等来表示函数． (3)f(x)与 f(a)的区别与联系：f(a)表示当 x＝a 时，函数 f(x)的值，是一个常量，而 f(x)是自变量 x 的函数，一般情况下，它是一个变量，f(a)是 f(x)的一个特殊值．如一次 函数 f(x)＝3x＋4，当 x＝8 时，f(8)＝3×8＋4＝28 是一个常数． y＝f(x)是“y 是 x 的函数”的数学表示，它也未必就是一个解析式，y＝f(a)表示自变 量 x＝a 时的函数值，它是一个常数；y＝f(x)是函数，通常是一个依赖于 x 变化而变化的变 量．函数还可以用其他一些符号来表示，例如：F(x)，G(x)，h(x)，…，也就是说，不管用 哪一个字母表示，它总是表达同样一个含义：y 是 x 的函数． 题型一 函数的概念 【例 1】 判断下列函数是否为同一函数： (1)f(x)＝|x| x 与 g(x)＝ 1，x≥0， －1，x＜0； (2)f(x)＝ x x＋1与 g(x)＝ x x＋1 ； (3)f(x)＝x2－2x－1 与 g(t)＝t2－2t－1； (4)f(x)＝1 与 g(x)＝x0(x≠0)． 分析：判断函数的定义域和对应关系是否一致． 反思：判断两个函数是否相同，只需判断这两个函数的定义域与对应关系是否相同． (1)定义域和对应关系都相同，则两个函数表示同一函数； (2)定义域不同，则两个函数不表示同一函数； (3)对应关系不同，则两个函数不表示同一函数； (4)即使定义域和值域都分别相同的两个函数，也不一定是同一函数，例如 y＝x 和 y＝ 2x－1 的定义域和值域都是 R，但不是同一函数； (5)两个函数是否相同，与自变量是什么字母无关． 题型二 求函数的定义域 【例 2】 求下列函数的定义域： (1)y＝2 x－ 1－7x； (2)y＝ x＋1 0 |x|－x . 分析：求函数的定义域就是求使函数表达式有意义的自变量的取值范围，可考虑列不等 式或不等式组． 反思：1.如果 f(x)是整式，那么函数的定义域是实数集 R. 2．如果 f(x)是分式，那么函数的定义域是使分母不等于零的实数的集合． 3．如果 f(x)是二次根式，那么函数的定义域是使根号内的式子大于或等于零的实数的 集合． 4．如果 f(x)是由几个部分的数学式子构成的，那么函数定义域是使各部分式子都有意 义的实数集合(即求各部分定义域的交集)． 5．对于由实际背景确定的函数，其定义域还要受实际问题的制约． 题型三 求函数值 【例 3】 已知 f(x)＝ 1 1＋x (x∈R，且 x≠－1)，g(x)＝x2＋2(x∈R)． (1)求 f(2)，g(2)的值； (2)求 f(g(2))的值． 分析：解决求值问题，先分清对应法则，再代入求值． 反思：(1)求函数值问题，首先确定出函数的对应法则 f 的具体含义，再代入求值． (2)求类似 f(g(2))的值，要注意 f，g 作用的对象，按“由内向外”的顺序求值． 题型四 求函数的值域 【例 4】 求下列各函数的值域： (1)y＝x＋1，x∈{2,3,4,5,6}； (2)y＝ x＋1； (3)y＝x2－4x＋6； (4)y＝x＋ 2x－1. 分析：确定函数的值域必须认真分析自变量 x 与对应法则之间的联系，关键是弄清自变 量变化时由对应法则确定函数值的变化规律． 反思：求函数值域的方法： (1)图像法：借助于函数值域的几何意义，利用函数的图像求值域； (2)观察法：对于解析式比较简单的函数，利用常见的结论如 x2≥0，|x|≥0， x≥0 等观察出函数的值域； (3)换元法：利用换元法转化为求常见函数如二次函数的值域等． 论函数的值域要先考虑函数的定义域，本例(1)中，如果忽视函数的定义域，那么会错 误地得出函数值域为 R.避免此类错误的方法是研究函数时要遵循定义域优先的原则． 题型五 易错辨析 易错点 求函数定义域时非等价化简解析式致错 【例 5】 求函数 y＝ x－2· x＋2的定义域． 错解：y＝ x－2· x＋2＝ x2－4，由 x2－4≥0，得 x≥2 或 x≤－2，∴函数的定义域 为{x|x≥2 或 x≤－2}． 错因分析：错解在求函数的定义域时，对函数的解析式进行了不等价变形，导致定义域 范围扩大． 答案：【例 1】 解：(1)f(x)的定义域中不含有元素 0，而 g(x)的定义域为 R，即定义 域不相同，所以不是同一函数． (2)f(x)的定义域为[0，＋∞)，而 g(x)的定义域为(－∞，－1]∪[0，＋∞)，定义域 也不相同，所以不是同一函数． (3)尽管两个函数的自变量一个用 x 表示，另一个用 t 表示，但它们的定义域相同，对 应关系相同，即对定义域内同一个自变量，根据表达式，都能得到同一函数值，因此二者为 同一函数． (4)f(x)的定义域为 R，g(x)的定义域为{x|x≠0}，因此也不是同一函数． 【例 2】 解：(1)令 x≥0， 1－7x≥0， 即 x≥0， x≤1 7 ， 所以 0≤x≤1 7 . 所以函数的定义域为 x|0≤x≤1 7 . (2)令 x＋1≠0， |x|－x>0， 即 x≠－1， x<0， 所以 x＜0 且 x≠－1. 所以函数的定义域为{x|x＜0 且 x≠－1}． 【例 3】 解：(1)∵f(x)＝ 1 1＋x ，∴f(2)＝ 1 1＋2 ＝1 3 ； 又 g(x)＝x2＋2，∴g(2)＝22＋2＝6. (2)f(g(2))＝f(6)＝ 1 1＋6 ＝1 7 . 【例 4】 解：(1)当 x 分别取 2,3,4,5,6 时，y＝x＋1 分别取 3,4,5,6,7，∴函数的值 域为{3,4,5,6,7}． (2)∵函数的定义域为[0，＋∞)， 当 x≥0 时， x≥0， ∴y≥1，即函数 y＝ x＋1 的值域为[1，＋∞)． (3)函数的定义域为 R. ∵y＝x2－4x＋6＝(x－2)2＋2≥2， ∴该函数的值域为[2，＋∞)． (4)换元法： 设 t＝ 2x－1，则 x＝t2＋1 2 且 t≥0. 问题转化为求 y＝1＋t2 2 ＋t(t≥0)的值域． ∵y＝1＋t2 2 ＋t＝1 2 (t＋1)2(t≥0)，(t＋1)2≥1， ∴y 的取值范围为 1 2 ，＋∞ . 故该函数的值域为 1 2 ，＋∞ . 【例 5】 正解：由 x－2≥0， x＋2≥0， 得 x≥2， x≥－2， 即 x≥2， ∴函数的定义域为{x|x≥2}． 1 下列四个图形中，不是．．以 x 为自变量的函数的图像是( )． 2 已知函数 f(x)＝ 1 1 x x + - ，则 f(2)等于( )． A．3 B．2 C．1 D．0 3 函数 y＝ 1 x x- + 的定义域为( )． A．{x|x≤1} B．{x|x≥0} C．{x|x≥1 或 x≤0} D．{x|0≤x≤1} 4 函数 y＝ 5 x ，x∈[1,5)的值域是__________． 5 判断下列各组的两个函数是否相等，并说明理由． (1)y＝x－1，x∈R 与 y＝x－1，x∈N； (2)y＝ 2x 与 y＝ x x× ； (3)y＝ 11 x + 与 u＝ 11 t + . 答案：1．C 2.A 3．D 要使函数有意义须 1 0, 0, x x     解得 0≤x≤1. 4. (1,5] 画出函数的图像，如图所示，观察图像得图像上所有点的纵坐标的取值范围 是(f(5)，f(1)]，则函数的值域是(1,5]． 5．解：(1)不相等．前者的定义域是 R，后者的定义域是 N，由于它们的定义域不同， 故不相等． (2)不相等．前者的定义域是 R，后者的定义域是{x|x≥0}，它们的定义域不同，故不 相等． (3)相等．定义域相同均为非零实数，对应关系相同，都是自变量取倒数后加 1，故相 等．