浙江省2021届高考数学一轮复习第三章函数概念及基本初等函数Ⅰ第2节二次函数课件 44页

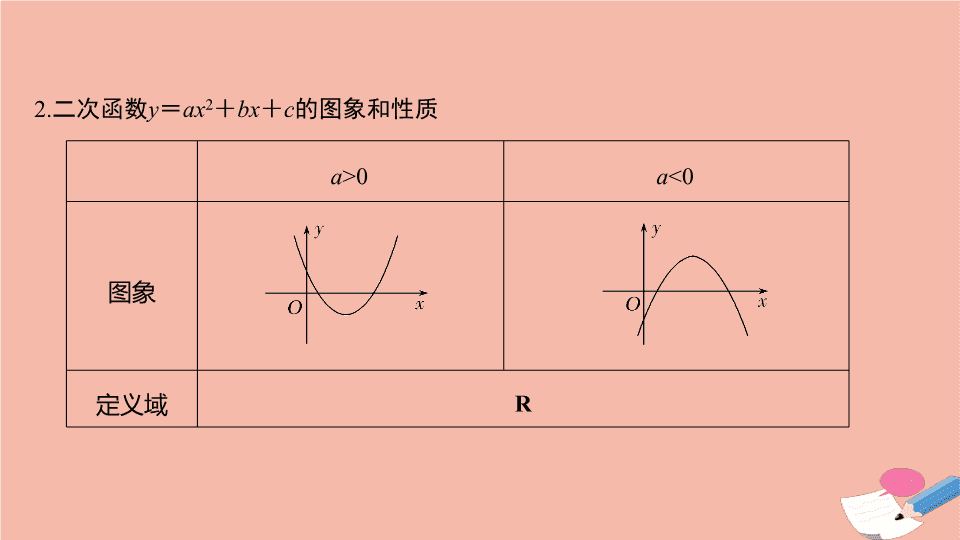
第 2 节　二次函数 考试要求　 1. 理解二次函数的图象和性质，能用二次函数、方程、不等式之间的关系解决简单问题； 2. 能解决一元二次方程根的分布问题； 3. 能解决二次函数的最值问题 . 知 识 梳 理 1 . 二次函数表达式的三种形式 (1) 一般式： y ＝ ax 2 ＋ bx ＋ c ( a ≠ 0). (2) 顶点式： y ＝ a ( x ＋ h ) 2 ＋ k ( 其中 a ≠ 0 ，顶点坐标为 ( － h ， k )). (3) 零点式： y ＝ a ( x － x 1 )( x － x 2 )( 其中 a ≠ 0 ， x 1 ， x 2 是二次函数的图象与 x 轴的两个交点的横坐标 ). 2 . 二次函数 y ＝ ax 2 ＋ bx ＋ c 的图象和性质   a >0 a <0 图象 定义域 R 3. 二次函数的最值问题 二次函数的最值问题主要有三种类型： “ 轴定区间定 ”“ 轴动区间定 ”“ 轴定区间动 ”. 解决的关键是弄清楚对称轴与区间的关系，要结合函数图象，依据对称轴与区间的关系进行分类讨论 . 设 f ( x ) ＝ ax 2 ＋ bx ＋ c ( a >0) ，则二次函数 f ( x ) 在闭区间 [ m ， n ] 上的最大值、最小值有如下的分布情况： 4. 一元二次方程根的分布 设方程 ax 2 ＋ bx ＋ c ＝ 0( a ≠ 0) 的不等两根为 x 1 ， x 2 且 x 1 < x 2 ，相应的二次函数为 f ( x ) ＝ ax 2 ＋ bx ＋ c ( a ≠ 0) ，方程的根即为二次函数图象与 x 轴的交点，它们的分布情况见下面各表 ( 每种情况对应的均是等价条件 ) 表一： ( 两根与 k 的大小比较 ) 表二：（根在区间上的分布） 若两根有且仅有一根在（ m ， n ）内，则需分三种情况讨论： ① 当 Δ ＝ 0 时，由 Δ ＝ 0 可以求出参数的值，然后再将参数的值代入方程，求出相应的根，检验根是否在给定的区间内，如若不在，舍去； ② 当 f （ m ）＝ 0 或 f （ n ）＝ 0 ，方程有一根为 m 或 n ，可以求出另外一根，从而检验另一根是否在区间（ m ， n ）内； ③ 当 f （ m ） · f （ n ） <0 时，则两根有且仅有一根在（ m ， n ）内 . 答案　（ 1 ） √ 　（ 2 ） √ 　（ 3 ） × 　（ 4 ） × 2. 已知 f （ x ）＝ x 2 ＋ px ＋ q 满足 f （ 1 ）＝ f （ 2 ）＝ 0 ，则 f （－ 1 ）的值是（　　） A.5 B. － 5 C.6 D. － 6 解析　 由 f （ 1 ）＝ f （ 2 ）＝ 0 知方程 x 2 ＋ px ＋ q ＝ 0 的两根分别为 1 ， 2 ，则 p ＝－ 3 ， q ＝ 2 ， ∴ f （ x ）＝ x 2 － 3 x ＋ 2 ， ∴ f （－ 1 ）＝ 6. 答案　 C 3. 若方程 x 2 ＋（ m ＋ 2 ） x ＋ m ＋ 5 ＝ 0 只有负根，则 m 的取值范围是（　　） A.[4 ，＋ ∞ ） B. （－ 5 ，－ 4] C.[ － 5 ，－ 4] D. （－ 5 ，－ 2 ） 答案　 A 4. 已知函数 y ＝ x 2 － 2 x ＋ 3 在闭区间 [0 ， m ] 上有最大值 3 ，最小值 2 ，则 m 的取值范围为（　　） A.[0 ， 1] B.[1 ， 2] C. （ 1 ， 2] D. （ 1 ， 2 ） 解析　 画出函数 y ＝ x 2 － 2 x ＋ 3 的图象（如图），由题意知 1 ≤ m ≤ 2. 答案　 B 5. 已知方程 x 2 ＋（ m － 2 ） x ＋ 2 m － 1 ＝ 0 的较小的实根在 0 和 1 之间，则实数 m 的取值范围是 　　　　 . 6. 若函数 f （ x ）＝ x 2 ＋ 2 （ a － 1 ） x ＋ 2 在区间（－ ∞ ， 3] 上是减函数，则实数 a 的取值范围是 　　　　 ，且函数 f （ x ）恒过点 　　　　　 . 解析　 二次函数 f （ x ）图象的对称轴是 x ＝ 1 － a ，由题意知 1 － a ≥ 3 ， ∴ a ≤ － 2. 由函数的解析式易得函数 f （ x ）恒过定点（ 0 ， 2 ） . 答案　（－ ∞ ，－ 2] 　（ 0 ， 2 ） 【例 1 】 求下列函数的解析式： （ 1 ） （一题多解） 已知二次函数 f （ x ）满足 f （ 2 ）＝－ 1 ， f （－ 1 ）＝－ 1 ，且 f （ x ）的最大值是 8 ； （ 2 ）已知二次函数 f （ x ）的图象经过点（ 4 ， 3 ），它在 x 轴上截得的线段长为 2 ，并且对任意 x ∈ R ，都有 f （ 2 － x ）＝ f （ 2 ＋ x ） . 考点一　二次函数的解析式 解　（ 1 ）法一 （利用一般式解题） 设 f （ x ）＝ ax 2 ＋ bx ＋ c （ a ≠ 0 ） . 法二（ 利用顶点式解题 ） 设 f （ x ）＝ a （ x － m ） 2 ＋ n （ a ≠ 0 ） . ∵ f （ 2 ）＝ f （－ 1 ）， 法三 （ 利用零点式解题 ） 由已知 f （ x ）＋ 1 ＝ 0 的两根为 x 1 ＝ 2 ， x 2 ＝－ 1 ， 故可设 f （ x ）＋ 1 ＝ a （ x － 2 ）（ x ＋ 1 ）（ a ≠ 0 ）， 即 f （ x ）＝ ax 2 － ax － 2 a － 1. ∴ 所求函数的解析式为 f （ x ）＝－ 4 x 2 ＋ 4 x ＋ 7. （ 2 ） ∵ f （ 2 － x ）＝ f （ 2 ＋ x ）对 x ∈ R 恒成立， ∴ f （ x ）的对称轴为 x ＝ 2. 又 ∵ f （ x ）的图象在 x 轴上截得的线段长为 2 ， ∴ f （ x ）＝ 0 的两根为 1 和 3. 设 f （ x ）的解析式为 f （ x ）＝ a （ x － 1 ）（ x － 3 ）（ a ≠ 0 ）， 又 ∵ f （ x ）的图象过点（ 4 ， 3 ）， ∴ 3 a ＝ 3 ， ∴ a ＝ 1. ∴ 所求 f （ x ）的解析式为 f （ x ）＝（ x － 1 ）（ x － 3 ）， 即 f （ x ）＝ x 2 － 4 x ＋ 3. 规律方法 　用待定系数法求二次函数的解析式，关键是灵活选取二次函数解析式的形式，选法如下： 【训练 1 】 若函数 f （ x ）＝（ x ＋ a ）（ bx ＋ 2 a ）（常数 a ， b ∈ R ）是偶函数，且它的值域为（－ ∞ ， 4] ，则该函数的解析式 f （ x ）＝ 　　　　 . 解析　 由 f （ x ）是偶函数知 f （ x ）的图象关于 y 轴对称， ∴ b ＝－ 2 ， ∴ f （ x ）＝－ 2 x 2 ＋ 2 a 2 ，又 f （ x ）的值域为（－ ∞ ， 4] ， ∴ 2 a 2 ＝ 4 ，故 f （ x ）＝－ 2 x 2 ＋ 4. 答案　 － 2 x 2 ＋ 4 考点二　二次函数的图象与性质 【例 2 】 已知函数 f （ x ）＝ x 2 ＋ 2 ax ＋ 3 ， x ∈ [ － 4 ， 6]. （ 1 ）当 a ＝－ 2 时，求 f （ x ）的最值； （ 2 ）求实数 a 的取值范围，使 y ＝ f （ x ）在区间 [ － 4 ， 6] 上是单调函数； （ 3 ）当 a ＝－ 1 时，求 f （ | x | ）的单调区间 . 解　 （ 1 ）当 a ＝－ 2 时， f （ x ）＝ x 2 － 4 x ＋ 3 ＝（ x － 2 ） 2 － 1 ，由于 x ∈ [ － 4 ， 6] ， ∴ f （ x ）在 [ － 4 ， 2] 上单调递减，在 [2 ， 6] 上单调递增， ∴ f （ x ）的最小值是 f （ 2 ）＝－ 1 ， 又 f （－ 4 ）＝ 35 ， f （ 6 ）＝ 15 ，故 f （ x ）的最大值是 35. （ 2 ）由于函数 f （ x ）的图象开口向上，对称轴是 x ＝－ a ，所以要使 f （ x ）在 [ － 4 ， 6] 上是单调函数，应有－ a ≤ － 4 或－ a ≥ 6 ，即 a ≤ － 6 或 a ≥ 4 ， 故 a 的取值范围是（－ ∞ ，－ 6] ∪ [4 ，＋ ∞ ） . （ 3 ）由－ 4 ≤ | x | ≤ 6 ，得－ 6 ≤ x ≤ 6 ，当 a ＝－ 1 时， f （ | x | ）＝ x 2 － 2| x | ＋ 3 其图象如图所示， ∴ f （ | x | ）在 [ － 6 ， 6] 上的单增区间为 [ － 1 ， 0] 和 [1 ， 6] ，单减区间为 [ － 6 ，－ 1 ）和（ 0 ， 1 ） . 规律方法 　解决二次函数图象与性质问题时要注意： （ 1 ）抛物线的开口、对称轴位置、定义区间三者相互制约，常见的题型中这三者有两定一不定，要注意分类讨论； （ 2 ）要注意数形结合思想的应用 . 【训练 2 】 （ 1 ）设 abc >0 ，二次函数 f （ x ）＝ ax 2 ＋ bx ＋ c 的图象可能是（　　） （ 2 ）若函数 f （ x ）＝ ax 2 ＋ 2 x ＋ 3 在区间 [ － 4 ， 6] 上是单调递增函数，则实数 a 的取值范围是 　　　　 . 考点三　二次函数的最值 【例 3 － 1 】 已知函数 f （ x ）＝ ax 2 ＋ 2 ax ＋ 1 在区间 [ － 1 ， 2] 上有最大值 4 ，求实数 a 的值 . 解　 f （ x ）＝ a （ x ＋ 1 ） 2 ＋ 1 － a . （ 1 ）当 a ＝ 0 时，函数 f （ x ）在区间 [ － 1 ， 2] 上的值为常数 1 ，不符合题意，舍去； 【例 3 － 2 】 将例 3 － 1 改为：求函数 f （ x ）＝ x 2 ＋ 2 ax ＋ 1 在区间 [ － 1 ， 2] 上的最大值 . 解　 f （ x ）＝（ x ＋ a ） 2 ＋ 1 － a 2 ， ∴ f （ x ）的图象是开口向上的抛物线，对称轴为 x ＝－ a ， 规律方法　 研究二次函数的性质，可以结合图象进行；对于含参数的二次函数问题，要明确参数对图象的影响，进行分类讨论 . 【训练 3 】 设函数 f （ x ）＝ x 2 － 2 x ＋ 2 ， x ∈ [ t ， t ＋ 1] ， t ∈ R ，求函数 f （ x ）的最小值 . 解　 f （ x ）＝ x 2 － 2 x ＋ 2 ＝（ x － 1 ） 2 ＋ 1 ， x ∈ [ t ， t ＋ 1] ， t ∈ R ，函数图象的对称轴为 x ＝ 1. 当 t ＋ 1<1 ，即 t <0 时，函数图象如图（ 1 ）所示，函数 f （ x ）在区间 [ t ， t ＋ 1] 上为减函数，所以最小值为 f （ t ＋ 1 ）＝ t 2 ＋ 1 ； 当 t ≤ 1 ≤ t ＋ 1 ，即 0 ≤ t ≤ 1 时，函数图象如图（ 2 ）所示，在对称轴 x ＝ 1 处取得最小值，最小值为 f （ 1 ）＝ 1 ； 当 t >1 时，函数图象如图（ 3 ）所示，函数 f （ x ）在区间 [ t ， t ＋ 1] 上为增函数， 所以最小值为 f （ t ）＝ t 2 － 2 t ＋ 2. 考点四　一元二次方程根的分布 角度 1 　两根在同一区间 【例 4 － 1 】 若二次函数 y ＝－ x 2 ＋ mx － 1 的图象与两端点为 A （ 0 ， 3 ）， B （ 3 ， 0 ）的线段 AB 有两个不同的交点，求实数 m 的取值范围 . 多维探究 由题意可得，方程 ① 在 x ∈ [0 ， 3] 内有两个不同的实根，令 f （ x ）＝ x 2 －（ m ＋ 1 ） x ＋ 4 ， 角度 2 　两根在不同区间 【例 4 － 2 】 求实数 m 的取值范围，使关于 x 的方程 x 2 ＋ 2 （ m － 1 ） x ＋ 2 m ＋ 6 ＝ 0. （ 1 ）一根大于 1 ，另一根小于 1 ； （ 2 ）两根 α ， β 满足 0< α <1< β <4 ； （ 3 ）至少有一个正根 . 解得－ 3< m < － 1. 当方程有一个正根一个负根时， f （ 0 ）＝ 2 m ＋ 6<0 ，解得 m < － 3. 当方程有一个根为零时， f （ 0 ）＝ 2 m ＋ 6 ＝ 0 ，解得 m ＝－ 3 ， 此时 f （ x ）＝ x 2 － 8 x ，另一根为 8 ，满足题意 . 综上可得，实数 m 的取值范围是（－ ∞ ，－ 1 ） . 角度 3 　在区间（ m ， n ）内有且只有一个实根 【例 4 － 3 】 已知函数 f （ x ）＝ mx 2 － 2 x ＋ 1 有且仅有一个正实数的零点，求实数 m 的取值范围 . 解　 依题意，得 解得 m ＝ 1 ，经验证，满足题意 . 又当 m ＝ 0 时， f （ x ）＝－ 2 x ＋ 1 ，它显然有一个为正实数的零点 . 综上所述， m 的取值范围是（－ ∞ ， 0] ∪ {1}. 规律方法　 利用二次函数图象解决方程根的分布的一般步骤： （ 1 ）设出对应的二次函数； （ 2 ）利用二次函数的图象和性质列出等价不等式（组）； （ 3 ）解不等式（组）求得参数的范围 . 【训练 4 】 （ 1 ）已知二次函数 y ＝（ m ＋ 2 ） x 2 －（ 2 m ＋ 4 ） x ＋（ 3 m ＋ 3 ）与 x 轴有两个交点，一个大于 1 ，一个小于 1 ，求实数 m 的取值范围 . （ 2 ）若关于 x 的方程 x 2 ＋ 2 （ m － 1 ） x ＋ 2 m ＋ 6 ＝ 0 有且只有一根在区间（ 0 ， 3 ）内，求实数 m 的取值范围 . 解　 （ 1 ）令 f （ x ）＝（ m ＋ 2 ） x 2 －（ 2 m ＋ 4 ） x ＋（ 3 m ＋ 3 ） . 由题意可知（ m ＋ 2 ） · f （ 1 ） <0 ， （ 2 ）令 f （ x ）＝ x 2 ＋ 2 （ m － 1 ） x ＋ 2 m ＋ 6 ， ③ f （ 0 ）＝ 2 m ＋ 6 ＝ 0 ，即 m ＝－ 3 时， f （ x ）＝ x 2 － 8 x ，另一根为 8 ∉ （ 0 ， 3 ），所以舍去；