浙江省台州市2020届高三下学期4月教学质量评估数学试题 Word版含解析 27页

- 1 - 台州市 2020 年 4 月高三年级教学质量评估试题数学 一、选择题：本大题共 10 小题，每小题 4 分，共 40 分.在每小题给出的四个选项中，只有一 项是符合题目要求的. 1.已知全集  1,2,3,4,5U  ，若集合  1,2,3A  ，  3,4B  ，则 U A B ð （ ） A.  B.  4 C.  3 D.  3,4,5 【答案】B 【解析】 【分析】 先求出  4, 5UC A  ,再求   4UC A B  ，从而得到答案. 【详解】由全集  1,2,3,4,5U  ，集合  1,2,3A  ,得  4, 5UC A  . 又  3,4B  ，则    4UC A B  故选：B 【点睛】本题考查求集合的补集和交集运算，属于基础题. 2.已知复数 z 满足 3 4i iz  （其中i 为虚数单位），则 z  （ ） A. 25 B. 1 25 C. 5 D. 1 5 【答案】D 【解析】 【分析】 由 3 4i iz  先求出复数 z ，再求 z . 【详解】由 3 4i iz  ,得      3 4 4 3 3 4 3 4 3 4 25 i ii iz i i i        则 2 24 3 5 1+ =25 25 25 5z            故选：D 【点睛】本题考查复数的除法运算和求模长，属于基础题. 3.已知 a ，bR ，则“3 3a b ”是“ 3 3a b ”的（ ） A. 充分不必要条件 B. 必要不充分条件 - 2 - C. 充要条件 D. 既不充分也不必要条件 【答案】C 【解析】 【分析】 由函数 33 ，xy y x 在 R 上是单调递增函数，则 3 33 3a b aa b b   可得答案. 【详解】由函数 33 ，xy y x 在 R 上是单调递增函数， 所以 3 33 3a b aa b b   即当 3 3a b 时， 3 3a b 成立，反之当 3 3a b 时， 3 3a b 成立 所以“3 3a b ”是“ 3 3a b ”的充要条件. 故选：C 【点睛】本题考查函数的单调性的应用和充要条件的判断，属于基础题. 4.若实数 x ， y 满足 1 2, 3 2 5, x y x y        则3x y 的最大值为（ ） A. 7 B. 8 C. 9 D. 10 【答案】C 【解析】 【分析】 由条件 1 2, 3 2 5, x y x y        作出可行域，目标函数中 z 表示直线 3y x z   在 y 轴上的截距，根 据可行域可以得到直线 3y x z   在 y 轴上截距的最大值，从而得到答案. 【详解】由条件 1 2, 3 2 5, x y x y        作出可行域，如图. 由 1 3=2 x y x y     得点  2, 1A  , 由 1 5=2 x y x y     得点  4, 3B  由 2 3=2 x y x y     得点  1,1C , 由 2 5=2 x y x y     得点  3, 1D  设目标函数 z 3x y  ，则变形为 3y x z   . - 3 - 所以目标函数中 z 表示直线 3y x z   在 y 轴上的截距. 根据可行域，可得当直线 3y x z   过点  4, 3B  时，在 y 轴上的截距最大. 所以 z 的最大值为3 4 3=9  故选：C 【点睛】本题考查简单的线性规划问题，注意目标函数的几何意义，属于中档题. 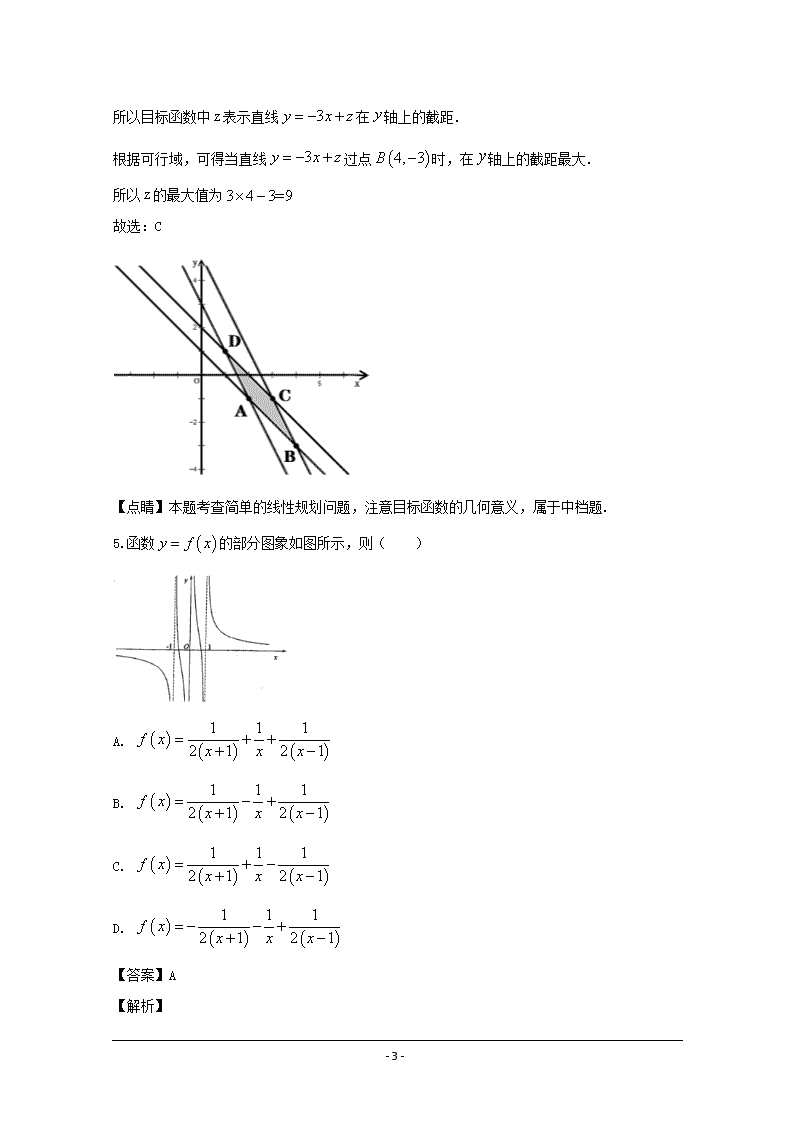5.函数  y f x 的部分图象如图所示，则（ ） A.       1 1 1 2 1 2 1xf x x x     B.       1 1 1 2 1 2 1xf x x x     C.       1 1 1 2 1 2 1xf x x x     D.       1 1 1 2 1 2 1xf x x x      【答案】A 【解析】 - 4 - 【分析】 由函数图象的对称性可得，函数为奇函数，再根据当 0x  且 0x  时，   0f x  ，可得答 案. 【详解】由函数图象的对称性可得，函数  y f x 为奇函数. 在选项 C 中，       2 1 1 1 1 1 2 1 2 1 1f x x x x x x        ,    1 1 1 12 2 +2 3 2 3f f        不是奇函数，所以排除. 在选项 D 中，       2 1 1 1 1 1 2 1 2 1 1x x x xf x x         ,    1 1 1 12 + 23 2 2 3f f      不是奇函数，所以排除. 在选项 B 中.        2 2 1 1 1 1 2 1 2 1 1 1 1x x x x x x x x f x               2 1 1x x f x f x      是奇函数, 由    2 1 1x f x x   ，当 0x  且 0x  时，   0f x  ，不满足条件，所以排除. 故选：A 【点睛】本题考查根据函数图象选择解析式，考查函数的基本性质，注意在选择题中排除法 的应用，属于中档题. 6.已知数列 na 满足：   1 2 1 1 n n na a n     （ n N ），若 6 5a  ，则 1a  （ ） A. 26 B. 0 C. 5 D. 26 【答案】B 【解析】 【分析】 由 递 推 关 系   1 2 1 1 n n na a n     得 2 1 2 2 4kka a k   ，  2 2 2 +2 12 +1 4 4 12kk k ka a k     ，将两式相减得 22 2 4 1k ka a k    ，由 6 5a  可得 4 4a  ，从而得出 2 1a  ，进一步得到答案. - 5 - 【详解】由   1 2 1 1 n n na a n     ，当 2 ,n k k Z  时，有 2 1 2 2 4kka a k   ……………① 当 2 1,n k k Z   时，有  2 2 2 +2 12 +1 4 4 12kk k ka a k     ……………② 由②－①可得 22 2 4 1k ka a k    所以当 2k  时有： 6 4 9a a  ，又 6 5a  ，则 4 4a  当 1k  时有： 4 2 5a a  ，则 2 1a  又当 1n  时， 2 1 1a a  ，所以 1 0a  . 故选：B 【点睛】本题考查递推数列，由递推数列的递推关系求数列中的项，属于中档题. 7.5G 技术的数学原理之一便是著名的香农公式： 2log 1 SC W N      .它表示：在受噪声干挠 的信道中，最大信息传递速率C 取决于信道带宽W 、信道内信号的平均功率 S 、信道内部的 高斯噪声功率 N 的大小，其中 S N 叫做信噪比.按照香农公式，若不改变带宽W ，而将信噪比 S N 从 1000 提升至 2000，则C 大约增加了（ ） A. 10% B. 30% C. 50% D. 100% 【答案】A 【解析】 【分析】 由 C 大约增加的百分比为       2 2 2 2 2 log 1 2000 log 1 1000 1+log 11 lg2log 1 1000 lo 1000 1000g 3 W W W       ，再根 据 11 341 1lg10 lg 2 lg104 3     ，可以估算出答案. 【详解】当 1000S N  时，  2log 1 1000C W  当 2000S N  时，  2log 1 2000C W  则       2 2 2 2 2 2 2 20log 1 2000 log 1 1000 log 1+log 11 1 lg 2log 1 1000 log log 01 1000 1001 1000 3 W W W         - 6 - 又 11 341 1lg10 lg 2 lg104 3     ，根据选项分析， 1 lg 2 0.13  所以信噪比 S N 从 1000 提升至 2000，则C 大约增加了 10%. 故选：A 【点睛】本题考查一个量的增加的百分比的计算方法，考查估算法，属于中档题. 8.已知 1F ， 2F 分别为双曲线 2 2 19 16 x y  的左右焦点，以 2F 为圆心的圆与双曲线的渐近线相 切，该圆与双曲线在第一象限的交点为 P ，则 1 2F PF 的面积为（ ） A. 16 6 B. 12 6 C. 8 6 D. 4 6 【答案】C 【解析】 【分析】 根据条件可得 2 4PF  ，由双曲线的定义可得 1 10PF  ，又 1 2 10F F  ，所以 1 2F F P 为等 腰三角形，可求出其面积. 【详解】双曲线 2 2 19 16 x y  的渐近线方程为 4 3y x  . 则焦点  2 5,0F 到渐近线的距离为 2 2 4 5 4 3 4 d    因为以 2F 为圆心的圆与双曲线的渐近线相切，所以 4r  所以 2 4PF  ,由双曲线的定义有 1 10PF  又 1 2 10F F  - 7 - 所以 1 2F F P 为等腰三角形，则边 2PF 上的高为 2 2 2 1 100 4 4 62 PFPF         所以 1 2 1= 4 4 6 8 62F PFS    故选：C 【点睛】本题考查双曲线的基本性质，求三角形的面积，属于中档题. 9.平面向量 a ，b ， c ， d 满足 2a b  ， 3b c   ， 4c d  ， 5d a   ，则    a c b d      （ ） A. 14 B. 14 C. 7 D. 7 【答案】D 【解析】 【分析】 由    a c b d a b c d c b a d                      ， 将 2a b  ， 3b c   ， 4c d  ， 5d a   ，分别平方，然后结合所求可得出答案. 【详解】    a c b d a b c d c b a d                      由 2a b  可得 2 2 2 4a a b b       ……………① 3b c   可得 2 2 2 9b b c c       ……………② 4c d  可得 2 2 2 16c c d d       ……………③ 5d a   可得 2 2 2 25d d a a       ……………④ 由②+④-(①+③) 可得  2 14a b c d c b a d               所以   a c b d      7 故选: D 【点睛】本题考查数量积的运算法则，向量模的处理技巧，属于中档题. 10.已知函数   2f x x px q   ，满足 02 2 p pf       ，则（ ） - 8 - A. 函数   y f f x 有 2 个极小值点和 1 个极大值点 B. 函数   y f f x 有 2 个极大值点和 1 个极小值点 C. 函数   y f f x a  有可能只有一个零点 D. 有且只有一个实数 a ，使得函数   y f f x a  有两个零点 【答案】A 【解析】 【分析】       22 2f f x x px q p x px q q       ,则     22 2 2 ph x x p x px q         ， 由 02 2 p pf       ，方程 2 02 px px q    有两个不等实数根 1 2,x x ，则设 1 22 px x   ， 可得出函数   f f x 的单调性，从而可判断出答案. 【详解】设         22 2h x f f x x px q p x px q q        所以         2 22 2 2 2 2 2 ph x x px q x p p x p x p x px q               设   2 2 pg x x px q    ，由 02 2 p pf       . 所以 02 2 2 p p pg f              ，因为二次函数  g x 的开口向上，对称轴方程为 2 px   . 所以方程 2 02 px px q    有两个不等实数根 1 2,x x ，则设 1 22 px x   . 则令   0h x  可得 1 2 px x   或 2x x . 令   0h x  可得 22 p x x   或 1x x . 所以函数     h x f f x 在 1，x 上单调递减，在 1 2 ， px    上单调递增，在 22 ，p x    上单调递减，在 2 +，x  上单调递增. 又当 ,x   x   时，    +f f x   ， - 9 - 又 2 2 1 1 2 2 02 2 p px px q x px q        ，所以 2 2 1 1 2 2 2 px px q x px q       由       22 2f f x x px q p x px q q       ，所以      1 2=f f x f f x 所以         1 2=f f x f f x f f x 根据单调性可知，函数   f f x 有 2 个极小值点和 1 个极大值点，所以选项 A 正确，B 不正 确. 根据函数的单调性，可画出函数   f f x 的大致草图如下. 当   1a f f x 时，函数   y f f x a  没有零点 当   1a f f x 时，函数   y f f x a  有两个零点 当   1 2 pf f x a f f         时，函数   y f f x a  有四个零点 当 2 pa f f        时，函数   y f f x a  有三个零点 当 2 pa f f        时，函数   y f f x a  有两个零点 由上可知选项 C,D 都不正确. 故选：A 【点睛】本题考查函数的极值的个数的判断和零点个数的判断，属于难题. 二、填空题：本大题共 7 小题，多空题每题 6 分，单空题每题 4 分，共 36 分. 11.在二项式 61 x 的展开式中，含 3x 项的系数为______；各项系数之和为______.（用数字 作答） 【答案】 (1). 20 (2). 0 【解析】 - 10 - 【分析】 二项式 61 x 的展开式中的通项公式为  r+1 6 rrT C x  ，可得含 3x 项的系数，令 1x  可得 各项系数之和. 【详解】二项式 61 x 的展开式中的通项公式为  r+1 6 rrT C x  所以含 3x 项的系数为  33 6 1 20C    设 6 2 6 0 1 2 61 x a a x a x a x      令 1x  得 6 0 1 2 61 1 0a a a a       所以各项系数之和为 0 故答案为：(1). 20 (2). 0 【点睛】本题考查二项式定理的指定项的系数和所有项的系数之和，属于基础题. 12.某几何体的三视图如图所示（单位： cm ），则它的体积是______. 【答案】 9 3 2 【解析】 【分析】 由三视图可知，原几何体为四棱锥,根据锥体的体积公式可求出答案. 【详解】由三视图可知，原几何体为如图所示的四棱锥. 将该四棱锥补成三棱柱，则该三棱柱为正三棱柱 过点 B 作 BO AC 交 AC 于点O ，则由正三棱柱的性质可得 BO  平面 1ACC D 则 3 3 2BO  - 11 - 所以 1 1 2 4 3 3 9 3= 33 3 2 2 2V Sh      故答案为： 9 3 2 【点睛】本题考查根据三视图求原几何体的体积问题，属于中档题. 13.某同学从家中骑自行车去学校，途中共经过 6 个红绿灯路口.如果他恰好遇见 2 次红灯， 则这 2 次红灯的不同的分布情形共有______种：如果他在每个路口遇见红灯的概率均为 1 3 ， 用 表示他遇到红灯的次数，则  E   ______.（用数字作答） 【答案】 (1). 15 (2). 2 【解析】 【分析】 从经过的 6 个红绿灯路口中取出 2 个，即 2 6 15C  ,他遇到红灯的次数 满足二项分布，可得 答案. 【详解】他恰好遇见 2 次红灯的不同的分布情形共有 2 6 15C  他遇到红灯的次数 值为 0,1,2,3,4,5,6. 他在每个路口遇见红灯的概率均为 1 3 ,他遇到红灯的次数 满足二项分布. 即 16 3 ，B      所以   16 23E     故答案为：(1). 15 (2). 2 【点睛】本题考查组合问题和将实际问题转化为二项分布并求期望，属于中档题. - 12 - 14.如图，过 ( )1,0A ， 10, 2B    两点的直线与单位圆 2 2 1x y  在第二象限的交点为C ，则 点C 的坐标为______； 9sin 4AOC       ______. 【答案】 (1). 3 4,5 5     (2). 7 2 10 【解析】 【分析】 过 ( )1,0A ， 10, 2B    两点的直线方程为 2 1x y  ，将直线方程与圆的方程联立可求出点C 的 坐标，利用三角函数的定义有 4sin 5 yAOC r    ， 3cos 5 xAOC r     ，利用诱导公式和 正弦的差角公式可得 9sin sin cos cos sin4 4 4AOC AOC AOC           ，可得出答案. 【详解】过 ( )1,0A ， 10, 2B    两点的直线方程为 2 1x y  . 则由 2 2 2 1 1 x y x y      有 25 4 0y y  ，解得 4 5y  或 0y  (舍) 由 2 1x y  得 4 31 2 5 5x      所以点C 的坐标为 3 4,5 5     根据三角函数的定义有 4sin 5 yAOC r    ， 3cos 5 xAOC r     所以 9sin sin sin cos cos sin4 4 4 4AOC AOC AOC AOC                     - 13 - 4 2 3 2 7 2 5 2 5 2 10          故答案为： 7 2 10 【点睛】本题考查直线与圆联立求交点，考查三角函数的定义和诱导公式、正弦函数的差角 公式，属于中档题. 15.若函数   2 lg , 0, 2 , 0, x x f x x x x     则 10 10f f           ______；不等式    1f x f x  的解 集为______. 【答案】 (1). 3 4 (2).  3 3 3, 0,2 2         【解析】 【分析】 由 10 10 1lg10 10 2f         ，则可求出 10 10f f           的值.分段将函数  1f x ，  f x 表达式代出来，然后分段打开绝对值求解. 【详解】由 10 10 1lg10 10 2f         所以 210 1 1 1 3210 2 2 2 4f f f                                   当 0x  时，      1 lg 1 lgf x x x f x     ，显然成立. 当 0x  时，      1 lg 0 1 0f x f x     ，显然成立. 当 1 0x   时，    1 lg 1 0f x x    ，   2 2 0f x x x   ，此时无解. 当 1x   时,   2 2 2f x x x x x     ,    21 2 1 3f x x x x x       由    1f x f x  ，即  1 3 2x x x x    . 当 3x   时，即     1 3 2x x x x      ，解得 3 2x   ，所以不成立. 当 3 2x    时，即    1 3 2x x x x     ，解得 3 3 3+ 3 2 2x    - 14 - 所以此时满足条件的 x 范围是 3 3 22 x     , 当 2 1x    时,即    1 3 2x x x x    ，解得 3 2x   ， 所以此时满足条件的 x 范围是 32 2x    综上所述，不等式    1f x f x  的解集为  3 3 3, 0,2 2         . 故答案为：  3 3 3 3, , 0,4 2 2         . 【点睛】本题考查求函数值和解含绝对值的不等式，解含绝对值的不等式关键是打开绝对值 符号，本题还可以结合函数的图象求解，属于中档题. 16.在等差数列 na 中，若 2 2 1 19 10a a  ，则数列 na 的前 10 项和 10S 的最大值为______. 【答案】25 【解析】 【分析】 由 10 1 10 910 2S S a d   ，有 1 45 10 S da  ，所以 19 135 10 S da  ，代入 2 2 1 19 10a a  ， 因为 na 为等差数列，则其公差 d 一定存在，即关于公差 d 的方程一定有解.根据 0  可得 到答案. 【详解】设等差数列 na 的公差为 d . 10 1 10 910 2S S a d   ，则 1 10 9 4510 2 10 S dS a    所以 19 1 13518 10 S da a d    由 2 2 1 19 10a a  ，得      2 2 2 2 2 2 2 2 1 19 2 180 45 13545 135 100 100 100 S Sd dS d S da a        即 2 2 245 10 +180 +2 1000 0d Sd S   (*) 因为 na 为等差数列，则其公差 d 一定存在，即关于公差 d 的方程(*)一定有解. 所以    2 2 2180 4 45 10 2 1000 0S S        整理即 2 625S  ,即 25S  - 15 - 所以数列 na 的前 10 项和 10S 的最大值为 25. 故答案为：25 【点睛】本题考查等差数列的性质，考查方程思想，属于中档题. 17.如下图①，在直角梯形 ABCD 中， 90ABC CDB DAB       ， 30BCD   ， 4BC  ，点 E 在线段 CD 上运动.如下图②，沿 BE 将 BEC△ 折至 BEC△ ，使得平面 BEC  平面 ABED ，则 AC的最小值为______. 【答案】 19 4 3 【解析】 【分析】 过点 C 作 CO BE 交 BE 于 O ,由平面 BEC  平面 ABED ，则 CO  平面 ABED .设 C BE   ，0 60   , sin 4sinC O C B     ， cos 4cosBO C B    ,在三角 形 AOB 中 , 2 2 2 2 cosAO BO AB BO AB ABO     , 则 所 以 2 2 2 2 216sin 16cos 3 4 3sin2AC C O AO          ，可得出答案. 【详解】由 90ABC CDB DAB       ， 30BCD   ，则 2, 1, 3B D A D A B   过点C 作CO BE 交 BE 于O ,由平面 BEC  平面 ABED ，则CO  平面 ABED . 设 C BE   ， 0 60    则在直角三角形C OB 中， sin 4sinC O C B     ， cos 4cosBO C B    - 16 - 在三角形 AOB 中, 2 2 2 2 cosAO BO AB BO AB ABO     216cos 3 2 4cos 3 cos 2             216cos 3 4 3sin 2    所以 2 2 2 2 216sin 16cos 3 4 3sin2AC C O AO          19 4 3sin 2  由 0 60   ，所以当 45  时， 2AC 有最小值19 4 3 所以 AC的最小值为 19 4 3 故答案为： 19 4 3 【点睛】本题考查线面垂直的应用，考查余弦定理解三角形，考查空间线段的长度的最值.属 于难题. 三、解答题：本大题共 5 小题，共 74 分.解答应写出文字说明、证明过程或演算步骤. 18.已知函数   2 2cos 2 3sin cos sinx x xf xx    . （1）求函数  f x 的最小正周期和最大值； （2）问方程   2 3f x  在区间 11,6 6      上有几个不同的实数根？并求这些实数根之和. 【答案】（1）T  ，最大值 2；（2）4 个不同的实数根，之和为 10 3  【解析】 【分析】 (1)将函数  f x 化简得   2sin 2 6xf x       ，再根据周期公式求最小周期，利用三角函 数的有界性求最大值. (2)作出函数  f x 在区间 11,6 6      上的大致图像，可得方程的实数根的个数，再根据对称 性可求出这些实数根之和. 【详解】（1）因为   cos2 3sin 2 2sin 2 6x x xy f x         ， - 17 - 所以 2 2T    ， 当 2 26 2x k     ， k Z ，即 6x k   ， k Z 时， 函数  y f x 取得最大值 2. （2）由 2 26 2x k     ， k Z ，可得函数  f x 的对称轴为 2 6 kx    ， k Z ， 2 6x  0 2   3 2  2 x 12  3  7 12  5 6  13 12  y 0 -1 0 1 0 作出函数  f x 在 11,6 6      的大致图象如下， 所以方程   2 3f x  在区间 11,6 6      上共有 4 个不同的实数根， 且这些实数根关于 5 6x  对称，所以实根之和 10 3  . 【点睛】本题考查正弦函数的周期性、最值，正弦函数的图象的对称性，属于中档题. 19.如图， ABC 与等边 ABD△ 所在的平面相互垂直， //DE BC ， M 为线段 AD 中点，直 线 AE 与平面CBM 交于点 N . 2 2BC BA DE   ， 90ABC   . - 18 - （1）求证：平面CBMN  平面 ADE ； （2）求二面角 B CN A  的平面角的余弦值. 【答案】（1）见解析；（2） 2 4 【解析】 【分析】 (1)由条件可得 BC ⊥平面 ABD ，则 BC AD ，又 ABD△ 为等边三角形可得 BM AD ， 从而可得 AD  平面CBMN ，从而得证. (2)由条件可得 DE  平面CBMN ，即得到 DE BC MN  ，所以 N 为 AE 的中点，以 AB 中点O 为坐标原点， ,OB OD 为 ,x z 轴建立空间直角坐标系,用向量法求二面角的余弦值. 【详解】（1）证明：因为平面 ABC  平面 ABD ，且两平面交于 AB ， 90ABC   ， 所以 BC ⊥平面 ABD ，则 BC AD . 又因为 ABD△ 为等边三角形， M 为线段 AD 中点， 所以 BM AD . 因为 BC BM B ，所以 AD  平面CBMN ， 因为 AD 平面 ADE ，所以平面CBMN  平面 ADE （2）解：因为 DE BC‖ ， DE  平面CBMN ，且 BC 平面CBMN ， 所以 DE  平面CBMN ，因为平面 ADE  平面CBMN MN ， 所以 DE BC MN  ，所以 N 为 AE 的中点. 以 AB 中点O 为坐标原点， ,OB OD 为 ,x z 轴，建立空间直角坐标系，如图. - 19 - 根据已知可得：  1,0,0A  ，  1, 2,0C  ， 1 1 3, ,2 2 2N       ，  0,0, 3D ， 所以  2, 2,0AC   ， 1 1 3, ,2 2 2AN        ， 设平面 ACN 的法向量  1 , ,n x y z ， 由 1 1 0, 0, AC n AN n          可得 2 2 0, 1 1 3 0,2 2 2 x y x y z      取 1x  ，则 1y  ， 0z  ， 所以平面 ACN 的一个法向量  1 1,1,0n  ， 由（Ⅰ）得 AD  平面CBMN ， 所以平面CBMN 的一个法向量  2 1,0, 3n AD   ， 设二面角 B CN A  的大小为 ， 所以 1 1 2 2 1 2cos 42 2 n n n n          ， 所以二面角 B CN A  的平面角的余弦为 2 4 . 【点睛】本题考查面面垂直的证明，考查求二面角平面角的余弦值，求二面角的平面角多用 向量法，属于中档题. 20.已知数列 na ， nb 的前 n 项和分别为 nS ， nT ，且  1 34n nS a  ， 2 2 1 1 n n n Sb S   . （1）求数列 na ， nb 的通项公式； - 20 - （2）求证： 1 1 1 7 7 14nn T n   . 【答案】（1） 11 3 n na      ， 2 1 2 1 11 3 17 3 n n n b      ；（2）见解析 【解析】 【分析】 （1）由 na 与 nS 的递推关系  1 34n nS a  可求出 1 1 3n na a   ，得到数列 na 是等比数列， 从二得到答案. （ 2 ） 由 2 1 2 1 11 3 17 3 n n n b      , 知 1 7nb  ， 故 1 7nT n , 又   2 1 2 1 2 1 2 1 2 1 2 1 1 8 811 1 4 13 3 3 1 17 7 7 7 1 21 37 7 73 3 n n n n n n n b                   ,从而可证 1 1 7 14nT n  . 【详解】（1）解：因为  1 34n nS a  ，令 1n  得 1 1a  ， 当 2n  时，由  1 34n nS a  ，  1 1 1 34n nS a   两式相减得    1 1 13 34 4n n na a a     ，即 1 1 3n na a   ， 由此可知数列 na 是首项 1 为公比为 1 3  的等比数列， 故 11 3 n na      . 所以   11 3 1 134 4 4 3 n n nS a         ， 2 12 2 2 1 111 3 11 7 3 nn n n n Sb S      . （2）证明：由 2 1 2 1 11 3 17 3 n n n b      ,结合不等式的性质有 2 1 2 1 2 1 11 1 13 3 1 7 77 2 3 n n n n b          知 1 7nb  ，故 1 7nT n , - 21 - 又   2 1 2 1 2 1 2 1 2 1 2 1 1 8 811 1 4 13 3 3 1 17 7 7 7 1 21 37 7 73 3 n n n n n n n b                   ， 所以 1 2 3 2 1 1 1 1 4 1 1 1 7 7 7 21 3 3 3n nb b b                                ， 因为 3 2 1 1 1 1 1 1 33 113 3 3 9 81 9 n n          ，所以 1 4 3 1 7 21 8 14nT n    ， 综上， 1 1 1 7 7 14nn T n   . 【点睛】本题考查求数列的通项公式，利用放缩法证明数列不等式的问题，属于中档题. 21.如图，已知椭圆 1C ： 2 2 2 2 1y x a b   （ 0a b  ）的离心率为 2 2 ，并以抛物线 2C ： 2 8x y 的焦点 F 为上焦点.直线l ： y kx m  （ 0m  ）交抛物线 2C 于 A ， B 两点，分别以 A ， B 为切点作抛物线 2C 的切线，两切线相交于点 P ，又点 P 恰好在椭圆 1C 上. （1）求椭圆 1C 的方程； （2）求 mk 的最大值； （3）求证：点 F 恒在 AOB 的外接圆内. 【答案】（1） 2 2 18 4 y x  ；（2） 2 2 ；（3）见解析 【解析】 【分析】 （1）由条件有  0,2F ，即 2c  ，由离心率可得 2 2a  ，然后可求出b ，得到椭圆方程. - 22 - (2) 设  1 1,A x y ，  2 2,B x y ,将直线方程与抛物线方程联立，写出韦达定理， PA ：求出直 线 PA 的方程 2 1 1 4 8 x xy x  ，同理可得 PB ： 2 2 2 4 8 x xy x  ，可得到 1 2 1 2,2 8 x x x xP      ，根 据点 P 在椭圆，得到 2 232 8m k  ，利用均值不等式可到答案. (3) 因为过原点 O ，所以可设 AOB 的外接圆方程为 2 2 0x y Dx Ey    ,将  1 1,A x y ，  2 2,B x y 坐标代入圆的方程，求出 28 8E k m    ，将点  0,2F 代入外接圆方程可得  2 24 2 8 8 16 2 12k m k m       ，从而可证. 【详解】【详解】 （1）解：由已知得  0,2F ，所以 2c  ， 又因为 2 2 ce a   ，所以 2 2a  ， 所以椭圆 1C 的方程为 2 2 18 4 y x  . （2）设  1 1,A x y ，  2 2,B x y ，由直线 l ： y kx m  （ 0m  ）与抛物线 2C ： 2 8x y 方程 联立可得 2 8 8 0x kx m   ， 所以 1 2 1 2 2 8 , 8, 64 32 0, x x k x x k m          因为 4 xy  ，所以 PA ：   2 1 1 18 4 x xy x x   ，即 PA ： 2 1 1 4 8 x xy x  ， 同理可得 PB ： 2 2 2 4 8 x xy x  ， 由直线 PA 的方程与直线 PB 的方程联立有 2 2 2 2 1 1 4 8 4 8 x xy x x xy x       ，可得 1 2 2 x xx  将 1 2 2 x xx  代入直线 2 1 1 4 8 x xy x  可得 1 2 8 x xy  - 23 - 所以 1 2 1 2,2 8 x x x xP      ，即  4 ,P k m ， 因为点 P 在椭圆 2 2 18 4 y x  上，所以 2 216 18 4 m k  ， 即 2 232 8m k  . 因为 2 232 2 32m k mk  ， 所以当 2m  ， 2 4k  时， mk 取得最大值 2 2 . （3）证法：因为过原点O ，所以可设 AOB 的外接圆方程为 2 2 0x y Dx Ey    ， 由已知可得 2 2 1 1 1 1 2 2 2 2 2 2 0, 0 x y Dx Ey x y Dx Ey           故     4 4 2 2 1 2 2 12 2 2 2 1 2 2 11 2 1 2 2 1 2 1 2 2 1 2 2 11 2 2 1 64 8 x x x xx x x xx x y x x x y x E x x x xx y x y          3 3 1 2 2 21 2 1 2 1 2 2 1 8 8 8 8 x xx x x x x x x x        ， 所以 28 8E k m    ， 将点  0,2F 代入外接圆方程可得  2 24 2 8 8 16 2 12k m k m       ， 因为 0m  ，所以 216 2 12 0k m    ， 所以点 F 恒在 AOB 的外接圆内. 证法二：设 AOB 的外心为  ,Q QQ x y ， 由已知可得OA的中垂线为 2 1 1 1 8 16 2 x xy xx        ，即 3 1 1 18 416 xx y x x   ， 同理 OB 的中垂线为 3 2 2 28 416 xx y x x   ， 联立可得     3 3 1 2 1 2 1 2416Q x xx x y x x    - 24 - 所以   2 2 2 22 1 2 1 2 1 2 1 1 34 4 416 16 2 4Q xy x x x x x x                 ， 又因为  22 2 2Q Qx yFQ    ， 22 2 2 Q QR OQ x y   ， 所以 FQ OQ R  ， 所以点 F 恒在 AOB 的外接圆内. 【点睛】本题考查求椭圆的方程，抛物线的切线问题和椭圆、抛物线中的最值问题，圆与点 的位置关系的证明，属于难题. 22.已知函数   2exf x x  ，  g x ax . （1）求证：存在唯一的实数 a ，使得直线  y g x 与曲线  y f x 相切； （2）若  1,2a ，  0,2x ，求证：     2e 6f x g x   . （注： e 2.71828 为自然对数的底数.） 【答案】（1）见解析；（2）见解析 【解析】 【分析】 （ 1 ） 曲 线  y f x 在   ,t f t 处 的 切 线 为     2 2t ty e t e t x t     ， 所 以    2 e 2 , e e 2 , t t t a t t t t        只需证明  21 e 0tt t   有唯一解即可. (2) 要 证     2e 6f x g x   ， 即 证 2 2 26 e e e 6x x ax      , 设   2ex axF xa    ，即     2 2 2 2 6 e 1 e 6 6 e 2 e 6 F F          ，只要证明     2 2 1 e 6 2 6 e F F      ，然后构造函 数，讨论单调性，分析函数的最值，即可证明. 【 详 解 】 证 明 ：（ 1 ） 由   e 2xf x x   知 ， 在   ,t f t 处 的 切 线 为     2 2t ty e t e t x t     ， 当该直线为 y ax 时，可得    2 e 2 , e e 2 , t t t a t t t t        所以  21 e 0tt t   ，所以 1t  ， - 25 - 令     21 eth t t t   ，则当 1t  时，    e 2 0th t t    ， 所以  h t 在  1,t   单调递增， 而  1 1 0h    ，   22 e 4 0h    ，所以存在唯一的实数 t （  1,2t  ）， 使得   0h t  ，相应的 e 2ta t  也是唯一的， 即存在唯一-的实数 a ，使得直线  y g x 与曲线  y f x 相切. （2）要证     2e 6f x g x   ，即证 2 2 26 e e e 6x x ax      ， 令   2ex axF xa    ，对于确定的 x ，  F a 是一次函数，只要证明，     2 2 2 2 6 e 1 e 6, 6 e 2 e 6, F F          注意到对于同一  0,2x ，    1 2F F ，所以只要证明     2 2 1 e 6, 2 6 e , F F      ① ② 先证明①：记     21 exG x F x x    ，则   e 2 1x xG x    ， 令 e 2 1xy x   ，因为 e 2xy   ，所以 ln 20 xy   ， 由此可知  G x 在区间 0,ln 2 递减，在区间 ln 2,2 递增. 又因为  0 0G  ，   ln2e 2l 2l n 1 0n 2G     ，   22 e 5 0G    ， 所以，在区间 ln 2,2 上存在唯一实数 0x ，使得  0 0G x  . 故在区间 00, x ，  G x 递减，在区间 0 ,2x ，  G x 递增. 于是        2max max 0 , 2 e 6G x G G   .①得证. 再证明②：记     22 e 2xH x F x x    ， 当  0,1x 时，利用不等式 e 1x x  得，     2 2 22 1 1 1 11 1 6 ex x x xH x x               ； 当  1,2x 时，利用不等式 2 e 12 x x x   （ 0x  ）得 - 26 -     2 1 21 e ee e e 1 12 2 2 x x x x             ， 于是    2 2 2e e e e2 1 22 2 2 2x x xx xH x                  ， 其中二次函数   2e e1 22 2xx x        开口向上，对称轴为 2 22x e   ， 当  1,2x 时，  x 最小值为   e e 5e4 1 82 2 22 4          ， 所以       22 6 eH x x     . 综上，不等式①②均成立. 所以，当  0,2x ，对任意的  1,2a ，总有     2e 6f x g x   . 【点睛】本题考查曲线的切线问题，根据单调性分析方程的解，考查不等式的证明问题，考 查构造函数解决问题，属于难题. - 27 -