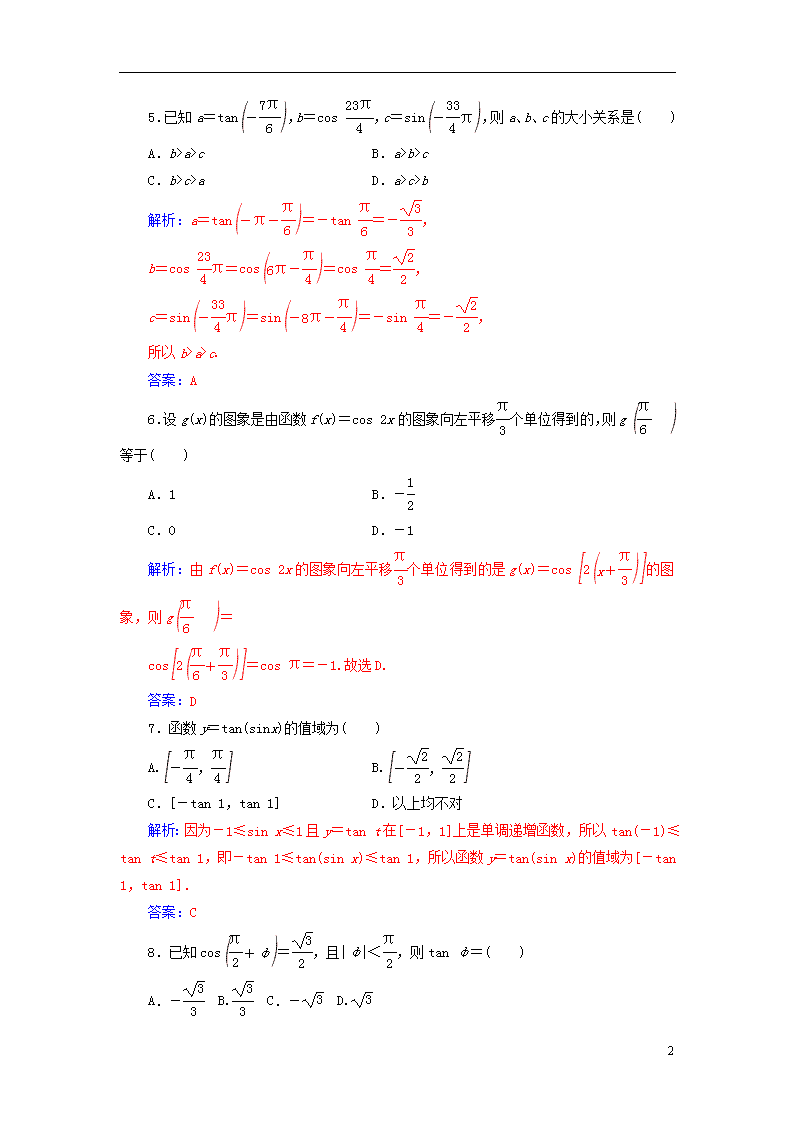2020年高中数学 第1章 三角函数单元评估验收 新人教A版必修4 9页

第1章 三角函数 单元评估验收(一)‎ ‎(时间：120分钟　满分：150分)‎ 一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)‎ ‎1．已知sin＝，则cos (π＋α)的值为(　　)‎ A. B．－ C. D．－ 解析：sin(－α)＝cos α＝，cos(π＋α)＝－cos α＝－.故选D.‎ 答案：D ‎2．已知2弧度的圆心角所对的弦长为2，那么这个圆心角所对的弧长为(　　)‎ A．2 B. C．sin 2 D．2sin 1‎ 解析：因为r＝，所以l＝αr＝.‎ 答案：B ‎3．已知角θ的终边过点(4，－3)，则cos(π－θ)＝(　　)‎ A. B．－ C. D．－ 解析：因为角θ的终边过点(4，－3)，‎ 所以cos θ＝.‎ 所以cos(π－θ)＝－cos θ＝－.‎ 答案：B ‎4．把函数f(x)＝sin 2x＋1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，得到函数g(x)的图象，则g(x)的最小正周期为(　　)‎ A．2π B．π C. D. 解析：由题意知g(x)＝sin＋1＝sin x＋1.故T＝2π.‎ 答案：A ‎5．已知a＝tan，b＝cos ，c＝sin，则a、b、c的大小关系是(　　)‎ 9‎ A．b>a>c B．a>b>c C．b>c>a D．a>c>b 解析：a＝tan＝－tan ＝－，‎ b＝cos π＝cos＝cos ＝，‎ c＝sin＝sin＝－sin ＝－，‎ 所以b>a>c.‎ 答案：A ‎6．设g(x)的图象是由函数f(x)＝cos 2x的图象向左平移个单位得到的，则g等于(　　)‎ A．1 B．－ C．0 D．－1‎ 解析：由f(x)＝cos 2x的图象向左平移个单位得到的是g(x)＝cos的图象，则g＝‎ cos＝cos π＝－1.故选D.‎ 答案：D ‎7．函数y＝tan(sinx)的值域为(　　)‎ A. B. C．[－tan 1，tan 1] D．以上均不对 解析：因为－1≤sin x≤1且y＝tan t在[－1，1]上是单调递增函数，所以tan(－1)≤tan t≤tan 1，即－tan 1≤tan(sin x)≤tan 1，所以函数y＝tan(sin x)的值域为[－tan 1，tan 1]．‎ 答案：C ‎8．已知cos＝，且|φ|＜，则tan φ＝(　　)‎ A．－ B. C．－ D. 解析：由cos＝，得sin φ＝－，又|φ|＜，所以cos φ＝，所以tan φ 9‎ ‎＝－.‎ 答案：C ‎9．要得到函数y＝sin x的图象，只需将函数y＝cos的图象上所有的点(　　)‎ A．横坐标伸长到原来的2倍(纵坐标不变)，再向左平移个单位长度 B．横坐标伸长到原来的2倍(纵坐标不变)，再向右平移个单位长度 C．横坐标伸长到原来的倍(纵坐标不变)，再向右平移个单位长度 D．横坐标伸长到原来的(纵坐标不变)，再向左平移个单位长度 解析：根据三角函数的平移变换可知横坐标伸长到原来的2倍(纵坐标不变)，函数表达式变为y＝cos(x－)，再向右平移个单位长度，函数表达式变为y＝cos(x－－)＝cos(x－)＝sin x.‎ 答案：B ‎10．函数y＝的图象与函数y＝sin πx(－2≤x≤4)的图象所有交点的横坐标之和等于(　　)‎ A．2 B．‎4 C．6 D．8‎ 解析：如图，两个函数的图象都关于点(1，0)成中心对称，两个图象在[－2，4]上共有8个交点，每两个对应交点横坐标之和为2，故所有交点的横坐标之和为8.‎ 答案：D ‎11．已知函数f(x)＝，则下列说法中正确的是(　　)‎ A．函数f(x)的周期是 B．函数f(x)的图象的一条对称轴方程是x＝ C．函数f(x)在区间上为减函数 D．函数f(x)是偶函数 9‎ 解析：当x＝时，f(x)＝1，所以x＝是函数图象的一条对称轴．‎ 答案：B ‎12．如果函数y＝3cos(2x＋φ)的图象关于点中心对称，那么|φ|的最小值为(　　)‎ A. B. C. D. 解析：由y＝3cos(2x＋φ)的图象关于点中心对称，知f＝0，‎ 即3cos(＋φ)＝0，‎ 所以＋φ＝kπ＋(k∈Z)，所以φ＝kπ＋－(k∈Z)，|φ|的最小值为.‎ 答案：A 二、填空题(本大题共4个小题，每小题5分，共20分．把答案填在题中的横线上)‎ ‎13．已知点P(tan α，cos α)在第三象限，则角α的终边在第________象限．‎ 解析：因为点P(tan α，cos α)在第三象限，‎ 所以tan α<0，cos α<0，则α是第二象限角．‎ 答案：二 ‎14．函数y＝2sin(3x＋φ)图象的一条对称轴为直线x＝，则φ＝________．‎ 解析：由y＝sin x的对称轴为x＝kπ＋(k∈Z)，可知3×＋φ＝kπ＋(k∈Z)，解得φ＝kπ＋(k∈Z)，又|φ|＜，所以k＝0，故φ＝.‎ 答案： ‎15．已知sin θ·cos θ＝，且＜θ＜，则cos θ－sin θ的值为________．‎ 解析：因为＜θ＜，所以cos θ－sin θ＜0，所以cos θ－sin θ＝－＝－＝－＝－.‎ 答案：－ ‎16．已知f(x)＝2sin－m在x∈上有两个不同的零点，则m 9‎ 的取值范围是________．‎ 解析：f(x)有两个零点，即m＝2sin，在上有两个不同的实根．‎ 当x∈时，‎ ‎2x－∈，结合正弦曲线知m∈[1，2)．‎ 答案：[1，2)‎ 三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤)‎ ‎17．(本小题满分10分)(1)设tan α＝－，求的值；‎ ‎(2)已知cos(75°＋α)＝，且－180°＜α＜－90°，求cos(15°－α)的值．‎ 解：(1)原式＝ ‎＝ ‎＝＝－1.‎ ‎(2)由－180°＜α＜－90°，得－105°＜α＋75°＜－15°，‎ 故sin(75°＋α)＝－＝－，‎ 而cos(15°－α)＝cos[90°－(75°＋α)]＝sin(75°＋α)，‎ 所以cos(15°－α)＝－.‎ ‎18．(本小题满分12分)已知函数f(x)＝2sin＋a，a为常数．‎ ‎(1)求函数f(x)的最小正周期；‎ ‎(2)若x∈时，f(x)的最小值为－2，求a的值．‎ 解：(1)f(x)＝2sin＋a.‎ 所以f(x)的最小正周期T＝＝π.‎ ‎(2)当x∈时，2x－∈，所以x＝0时，f(x)取得最小值，即2sin＋a＝－2，‎ 9‎ 故a＝－1.‎ ‎19．(本小题满分12分)(2015·湖北卷)某同学用“五点法”画函数f(x)＝Asin(ωx＋φ)在某一个周期内的图象时，列表并填入了部分数据，如下表：‎ ωx＋φ ‎0‎ π ‎2π x Asin(ωx＋φ)‎ ‎0‎ ‎5‎ ‎－5‎ ‎0‎ ‎(1)请将上表数据补充完整，并直接写出函数f(x)的解析式；‎ ‎(2)将y＝f(x)图象上所有点向左平行移动个单位长度，得到y＝g(x)的图象，求y＝g(x)的图象离原点O最近的对称中心．‎ 解：(1)根据表中已知数据，解得A＝5，ω＝2，φ＝－.数据补全如下表：‎ ωx＋φ ‎0‎ π ‎2π x Asin(ωx＋φ)‎ ‎0‎ ‎5‎ ‎0‎ ‎－5‎ ‎0‎ 且函数表达式为f(x)＝5sin.‎ ‎(2)由(1)知f(x)＝5sin，‎ 因此g(x)＝5sin＝5sin.‎ 因为y＝sin x的对称中心为(kπ，0)，k∈Z，‎ 令2x＋＝kπ，k∈Z，解得x＝－，k∈Z，‎ 即y＝g(x)图象的对称中心为，k∈Z，其中离原点O最近的对称中心为.‎ ‎20．(本小题满分12分)已知f(x)＝sin＋，x∈R.‎ ‎(1)求函数f(x)的最小正周期和单调增区间；‎ ‎(2)函数f(x)的图象可以由函数y＝sin 2x(x∈R)的图象经过怎样的变换得到？‎ 9‎ 解：(1)T＝＝π，2kπ－≤2x＋≤2kπ＋，k∈Z知kπ－≤x≤kπ＋(k∈Z)．‎ 所以函数f(x)的最小正周期为π，单调递增区间为(k∈Z)．‎ ‎(2)变换情况如下：y＝sin 2x y＝sin y＝sin＋.‎ ‎21．(本小题满分12分)已知函数y＝Asin(ωx＋φ)(A>0，ω>0，|ω|<π)的一段图象如图所示．‎ ‎(1)求此函数的解析式；‎ ‎(2)求此函数在(－2π，2π)上的递增区间．‎ 解：(1)由图可知，其振幅为A＝2，‎ 由于＝6－(－2)＝8，‎ 所以周期为T＝16，‎ 所以ω＝＝＝，‎ 此时解析式为y＝2sin.‎ 因为点(2，－2)在函数y＝2sin的图象上，‎ 所以×2＋φ＝2kπ－，所以φ＝2kπ－(k∈Z)．‎ 又|φ|<π，所以φ＝－.‎ 故所求函数的解析式为y＝2sin.‎ 9‎ ‎(2)由2kπ－≤x－≤2kπ＋(k∈Z)，得16k＋2≤x≤16k＋10(k∈Z)，‎ 所以函数y＝2sin的递增区间是[16k＋2，16k＋10](k∈Z)．‎ 当k＝－1时，有递增区间[－14，－6]，当k＝0时，有递增区间[2，10]，‎ 与定义区间求交集得此函数在(－2π，2π)上的递增区间为(－2π，－6]和[2，2π]．‎ ‎22．(本小题满分12分)设函数f(x)＝sin(2x＋φ)(－π<φ<0)，y＝f(x)的图象的一条对称轴是直线x＝.‎ ‎(1)求φ；‎ ‎(2)求函数y＝f(x)的单调增区间；‎ ‎(3)画出函数y＝f(x)在区间[0，π]上的图象．‎ 解：(1)因为x＝是函数y＝f(x)的图象的对称轴，‎ 所以sin＝±1，即＋φ＝kπ＋，k∈Z.因此－π<φ<0，所以当k＝－1时得φ＝－.‎ ‎(2)由(1)知φ＝－，因此y＝sin.由题意得2kπ－≤2x－≤2kπ＋，k∈Z，解得kπ＋≤x≤kπ＋π，(k∈Z)‎ 所以函数y＝sin的单调增区间为：‎ ，k∈Z.‎ ‎(3)由y＝sin知：‎ 令z＝2x－π，x∈[0，π]‎ ‎①列表如下：‎ 9‎ x ‎0‎ π z ‎－ π ‎－ ‎0‎ π π y ‎－ ‎－1‎ ‎0‎ ‎1‎ ‎0‎ ‎－ ‎②描点连线得函数y＝f(x)在区间[0，π]上的图象如下：‎ 9‎