广东省佛山市2019-2020学年普通高中高三教学质量检测（一）数学理科试题（PDF版，含答案） 8页

高三教学质量检测(一)理科数学试题 第 1 页 共 4 页 2019～2020 学年佛山市普通高中高三教学质量检测(一) 数 学(理科) 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分 150 分．考试时间 120 分钟． 注意事项： 1．答卷前，考生要务必填写答题卷上的有关项目． 2．选择题每小题选出答案后，用 2B 铅笔把答案涂在答题卷相应的位置上． 3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卷各题目指定区域内；如需改 动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液，不按以上要求作答的答案无效． 4．请考生保持答题卷的整洁．考试结束后，将答题卷交回． 第Ⅰ卷(选择题 共 60 分) 一、选择题：本大题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四个选项中，只有一项是符合题 目要求的． 1．在复平面内，复数 5i 1+ 2i 对应的点位于（ ） A．第一象限 B．第二象限 C．第三象限 D．第四象限 2．已知集合  2 2 0A x x x    ，  | | 1B x x  ，则 A B I （ ） A． ( 2, 1)  B． ( 1,1) C． (0,1) D． (1,2) 3．已知 ,x y R ，且 0x y  ，则（ ） A． cos cos 0x y  B． cos cos 0x y  C． ln ln 0x y  D． ln ln 0x y  4．函数 ( )f x 的图像向左平移一个单位长度，所得图像与 exy  关于 y 轴对称，则 ( )f x  （ ） A． 1e x  B． 1e x  C． 1ex D． 1ex 5．希尔宾斯基三角形是一种分形，由波兰数学家希尔宾斯基在 1915 年提出，先作一个正三角形，挖去一 个“中心三角形”（即以原三角形各边的中点为顶点的三角形），然后在剩下的小三角形中又挖去一个 “中心三角形”，我们用白色代表挖去的 面积，那么黑三角形为剩下的面积（我 们称黑三角形为希尔宾斯基三角形）．在 如图第 3 个大正三角形中随机取点，则 落在黑色区域的概率为（ ） A． 3 5 B． 9 16 C． 7 16 D． 2 5 6．已知等比数列 na 满足 1 2 36a a  ， 1 3 24a a  ，则使得 1 2 na a aL 取得最大值的 n 为（ ） A．3 B． 4 C．5 D． 6 7．已知 为锐角， 3cos 5   ，则 πtan =4 2     （ ） A． 1 3 B． 1 2 C． 2 D．3 2020 年 1 月 7 日 高三教学质量检测(一)理科数学试题 第 2 页 共 4 页 8．已知双曲线 2 2 2 2: 1x yC a b   ，O 为坐标原点，直线 x a 与双曲线C 的两条渐近线交于 ,A B 两点，若 △OAB 是边长为 2 的等边三角形，则双曲线C 的方程为（ ） A． 2 2 13 x y  B． 2 2 13 yx   C． 2 2 112 4 x y  D． 2 2 14 12 x y  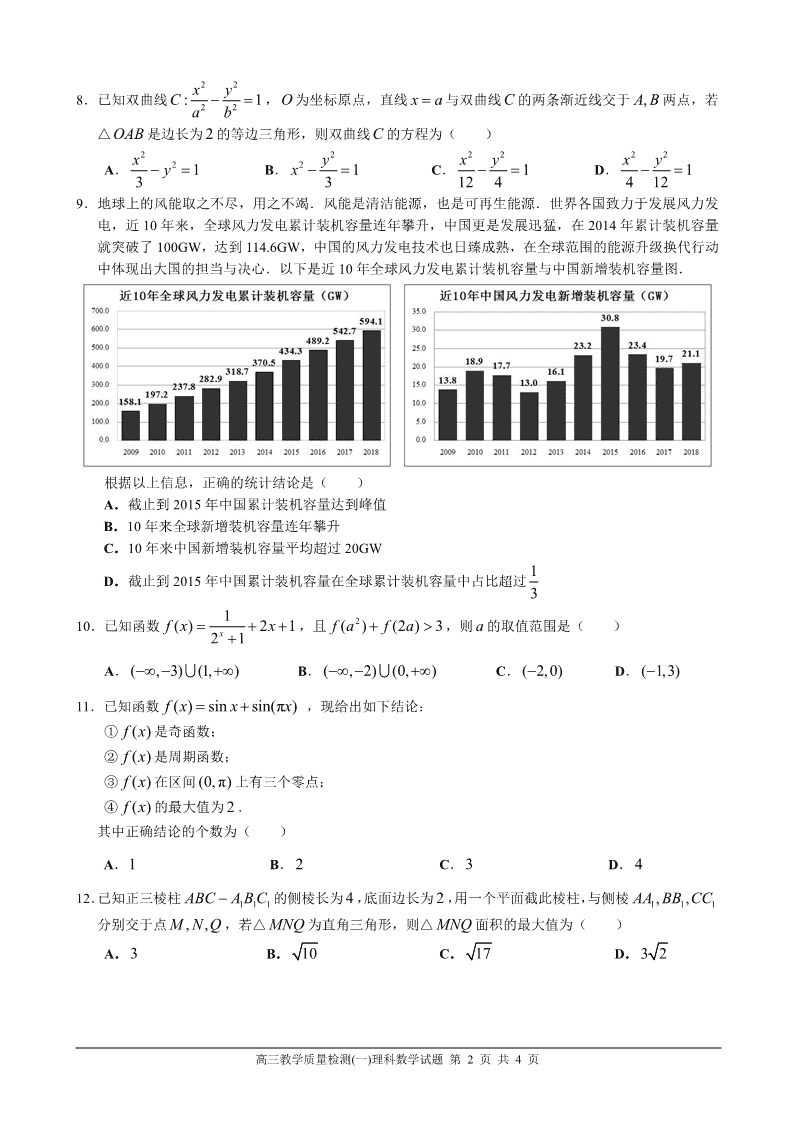9．地球上的风能取之不尽，用之不竭．风能是清洁能源，也是可再生能源．世界各国致力于发展风力发 电，近 10 年来，全球风力发电累计装机容量连年攀升，中国更是发展迅猛，在 2014 年累计装机容量 就突破了 100GW，达到 114.6GW，中国的风力发电技术也日臻成熟，在全球范围的能源升级换代行动 中体现出大国的担当与决心．以下是近 10 年全球风力发电累计装机容量与中国新增装机容量图． 根据以上信息，正确的统计结论是（ ） A．截止到 2015 年中国累计装机容量达到峰值 B．10 年来全球新增装机容量连年攀升 C．10 年来中国新增装机容量平均超过 20GW D．截止到 2015 年中国累计装机容量在全球累计装机容量中占比超过 1 3 10．已知函数 1( ) 2 12 1xf x x   ，且 2( ) (2 ) 3f a f a  ，则 a 的取值范围是（ ） A． ( , 3) (1, )  U B． ( , 2) (0, )  U C． ( 2,0) D． ( 1,3) 11．已知函数 ( ) sin sin(π )f x x x  ，现给出如下结论： ① ( )f x 是奇函数； ② ( )f x 是周期函数； ③ ( )f x 在区间 (0, π) 上有三个零点； ④ ( )f x 的最大值为 2 ． 其中正确结论的个数为（ ） A．1 B． 2 C．3 D． 4 12．已知正三棱柱 1 1 1ABC A B C 的侧棱长为 4 ，底面边长为 2 ，用一个平面截此棱柱，与侧棱 1 1 1, ,AA BB CC 分别交于点 , ,M N Q ，若△ MNQ 为直角三角形，则△ MNQ 面积的最大值为（ ） A．3 B． 10 C． 17 D．3 2 高三教学质量检测(一)理科数学试题 第 3 页 共 4 页 第Ⅱ卷(非选择题 共 90 分) 本卷包括必考题和选考题两部分．第 13～21 题为必考题，每个试题考生都必须作答．第 22～23 为选 考题，考生根据要求作答． 二、填空题：本大题共 4 小题，每小题 5 分，满分 20 分． 13．从进入决赛的 6 名选手中决出 1 名一等奖，2 名二等奖，3 名三等奖，则可能的决赛结果共有 种．（用数字作答） 14．在△ ABC 中， 2AB  ， 3AC  ， P 是边 BC 的垂直平分线上一点，则 AP BC  uuur uuur ． 15．函数 ( ) lnf x x 和 2( )g x ax x  的图象有公共点 P，且在点 P 处的切线相同，则这条切线方程为 ． 16．在平面直角坐标系 xOy 中，对曲线C 上任意一点 P ， P 到直线 1 0x   的距离与该点到点O 的距离 之和等于 2 ，则曲线C 与 y 轴的交点坐标是 ；设点 5 ,04A    ，则| | | |PO PA 的最小值 为 ． 三、解答题：本大题共 7 小题，共 70 分，解答须写出必要的文字说明、证明过程或演算步骤． 17．(本小题满分 12 分) 绿水青山就是金山银山．近年来，祖国各地依托本地自然资源，打造旅游产业，旅游业正蓬勃发展．景 区与游客都应树立尊重自然、顺应自然、保护自然的生态文明理念，合力使旅游市场走上规范有序且可持 续的发展轨道．某景区有一个自愿消费的项目：在参观某特色景点入口处会为每位游客拍一张与景点的合 影，参观后，在景点出口处会将刚拍下的照片打印出来，游客可自由选择是否带走照片，若带走照片则需 支付 20 元，没有被带走的照片会收集起来统一销毁。该项目运营一段时间后，统计出平均只有三成的游 客会选择带走照片．为改善运营状况，该项目组就照片收费与游客消费意愿关系作了市场调研，发现收费 与消费意愿有较强的线性相关性，并统计出在原有的基础上，价格每下调 1 元，游客选择带走照片的可能 性平均增加 0.05，假设平均每天约有 5000 人参观该特色景点，每张照片的综合成本为 5 元，假设每个游 客是否购买照片相互独立． （1）若调整为支付 10 元就可带走照片，该项目每天的平均利润比调整前多还是少？ （2）要使每天的平均利润达到最大值，应如何定价？ 18．(本小题满分 12 分) 在△ ABC 中，内角 A ， B ，C 的对边分别为 a ，b ， c ．已知 πsin sin( )3a B b A  ． （1）求 A ； （2） D 是线段 BC 上的点，若 2AD BD  ， 3CD  ，求△ ADC 的面积． 19．(本小题满分 12 分) 已知椭圆 2 2 2 2: 1( 0)x yC a ba b     的离心率为 1 2 ，点 31, 2A     在椭圆C 上，直线 1l 过椭圆C 的右焦 点与上顶点，动直线 2 :l y kx 与椭圆C 交于 ,M N 两点，交 1l 于 P 点． （1）求椭圆C 的方程； （2）已知O 为坐标原点，若点 P 满足 1 4OP MN ，求此时 MN 的长度． 高三教学质量检测(一)理科数学试题 第 4 页 共 4 页 20．(本小题满分 12 分) 如图，三棱锥 P ABC 中，平面 PAB  平面 ABC ，PA PB ， 90APB ACB     ，点 ,E F 分 别是棱 ,AB PB 的中点，点G 是△ BCE 的重心． （1）证明： / /GF 平面 PAC ； （2）若 GF 与平面 ABC 所成的角为 60 ，求二面角 B AP C  的余弦值． 21．(本小题满分12分) 已知函数 ( ) 1 2sin , 0f x x x x    ． （1）求 ( )f x 的最小值； （2）证明： 2( ) e xf x  ． 请考生在第 22，23 题中任选一题做答，如果多做，则按所做的第一题计分，做答时请写清楚题号． 22．(本小题满分 10 分)[选修 4 4 :坐标系与参数方程选讲] 在直角坐标系 xOy 中，曲线C 的参数方程为 24 4 x m y m     ( m 为参数)． （1）写出曲线C 的普通方程，并说明它表示什么曲线； （2）已知倾斜角互补的两条直线 1l ， 2l ，其中 1l 与C 交于 A ， B 两点， 2l 与C 交于 M ， N 两点， 1l 与 2l 交于点  0 0,P x y ，求证： PA PB PM PN   ． 23．(本小题满分 10 分)[选修 4 5 :不等式选讲] 已知函数 ( ) 1f x x a x    ． （1）若 ( ) 2f a  ，求 a 的取值范围； （2）当 [ , ]x a a k  时，函数 ( )f x 的值域为[1,3]，求 k 的值． 理科数学参考答案与评分标准 第 1页（共 4页） 2019~2020 年佛山市普通高中高三教学质量检测（一） 数 学(理科)参考答案与评分标准 一、选择题：本大题共 12 小题，每小题 5 分，满分 60 分． 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 A D C A B B D A D B B C 二、填空题：本大共 4 小题，每小题 5 分，满分 20 分． 13． 60 14． 5 2 15． 1y x  16．   70, 1 , 4  三、解答题：本大题共 6 小题，满分 70 分．解答须写出文字说明、证明过程或演算步骤． 17．【解析】（1）当收费为 20 元时，照片被带走的可能性为 0.3，不被带走的可能性为 0.7，设每个游客的 利润为 1Y (元)，则 1Y 是随机变量，其分布列为： 1Y 15 5 P 0.3 0.7 1( ) 15 0.3 5 0.7 1E Y      元，则 5000 个游客的平均利润为 5000 元； …………2 分 当收费为 10 元时，照片被带走的可能性为 0.3 0.05 10 0.8   ，不被带走的可能性为 0.2，设每个游客的 利润为 2Y (元)，则 2Y 是随机变量，其分布列为： 2Y 5 5 P 0.8 0.2 2( ) 5 0.8 5 0.2 3E Y      元，则 5000 个游客的平均利润为 15000 元； ………………5 分 该项目每天的平均利润比调整前多 10000 元． …………………………6 分 （2）设降价 x 元，则 0 15x  ，照片被带走的可能性为 0.3 0.05x ，不被带走的可能性为 0.7 0.05x ， 设每个游客的利润为Y (元)，则Y 是随机变量，其分布列为： Y 15 x 5 P 0.3 0.05x 0.7 0.05x 2( ) (15 ) (0.3 0.05 ) 5 (0.7 0.05 ) 0.05[69 ( 7) ]E Y x x x x          ……………………10 分 当 7x  时， ( )E Y 有最大值 3.45 元， ………………………………………11 分 即当定价为 13 元时，日平均利润为 17250 元． ……………………………………………12 分 18. 【解析】（1）由正弦定理，可得 sin sina B b A ． …………………………………………1 分 则有 1 3sin ( sin cos )2 2b A b A A  ，化简得 1 3sin cos2 2A A  ． …………………………3 分 即 tan 3A   ，∵ (0, π)A ，则 2π 3A  ． ……………………………………………………5 分 （2）设 π, (0, )3B     ， … ……4 分 … ……8 分 … ……1 分 理科数学参考答案与评分标准 第 2页（共 4页） 由题意得 BAD   ， 2ADC   ， 2π 3DAC    ， π 3ACD    ．……………………6 分 在△ ADC 中， sin sin CD AD DAC ACD   ，则 3 2 2π πsin( ) sin( )3 3      ． ………………………7 分 ∴ 3 2 3 1 3 1cos sin cos sin2 2 2 2        ，得 3sin cos5   ． ……………………………8 分 结合 2 2sin cos 1   ，可得 21sin 14   ， 5 7cos 14   ．………………………………………9 分 则 5 3sin 2 2sin cos 14     ． …………………………………………………………………10 分 ∴ 1 1 5 3 15 3sin 2 32 2 4 14ADCS AD CD ADC         ．………………………………………12 分 19．【解析】（1）由题意得 1 2 ce a   ， 2 2 2 3( )1 2 1a b   ，结合 2 2 2a b c  ， 解得 2 4a  ， 2 3b  ， 1c  ． …………………………………………………………………………3 分 故所求椭圆C 的方程为 2 2 14 3 x y  ． …………………………………………………………………4 分 （2）易知定直线 1l 的方程为 3 3 0x y   ． ……………………………………………………5 分 联立 2 2 14 3 y kx x y    ，整理得 2 2(3 4 ) 12k x  ，解得 2 12 3 4x k    ， 无妨令 M 点坐标为 2 2 12 12( , )3 4 3 4kk k  ． …………………………………………………………7 分 ∵ 1 4OP MN ，由对称性可知，点 P 为OM 的中点，故 P 点坐标为 2 2 12 12 3 4 3 4( , )2 2 kk k  ．…8 分 又 P 在直线 1 : 3 3 0l x y   上，故 2 2 12 12 3 4 3 43 3 02 2 kk k     ， 解得 1 2 2 30, 3k k  ．故 M 点坐标为 (2,0) 或 6 4 3( , )5 5 ． …………………………………………10 分 所以 2OM  或 2 21 5 ，所以 MN 的长度为 4 或 4 21 5 ． ……………………………………………12 分 理科数学参考答案与评分标准 第 3页（共 4页） 20.【解析】（1）连接 EF ，连接 EG 并延长交 BC 于点 D ，则点 D 为 BC 的中点， 从而点 , ,D E F 分别是棱 , ,CB AB PB 的中点，∴ / /DE AC ， / /EF AP ．…1 分 又 ,DE EF  平面 PAC ， ,AC AP  平面 PAC ． ∴ / /DE 平面 PAC ， / /EF 平面 PAC ． ……………………2 分 又 ,DE EF  平面 EFG ， DE EF E ，∴平面 / /EFG 平面 PAC ．…3 分 又GF  平面 EFG ，∴ / /GF 平面 PAC 。 ………………………………4 分 （2）连接 PE ，∵ PA PB ， E 是 AB 的中点，∴ PE  AB ，∵平面 PAB  平面 ABC ，平面 PAB  平面 ABC AB ， PE  平面 PAB ，∴ PE  平面 ABC ． …………………………………………6 分 连接 CG 并延长交 BE 于点O ，则O 为 BE 的中点，连接OF ，则 / /OF PE ，∴OF  平面 ABC ． ∴ FGO 为GF 与平面 ABC 所成的角，即 60FGO   ． …………………………………………7 分 在 Rt△ FGO 中，设 2GF  ，则 1OG  ， 3OF  ，∴ 3OC  ， 2 3PE  ． ∴ 4 3AB  ， 2 3CE  ， 3OE  ，∴ 2 2 2OE OC CE  ，即OC AB ． …………………8 分 如图建立空间直角坐标系O xyz ，则 (0, 3 3,0)A  ， (3,0,0)C ， (0, 3,2 3)P  ， ∴ (3,3 3,0)AC  ， (0,2 3,2 3)AP  ，设平面 PAC 的一个法向量为 1 ( , , )x y zn ， 则由 1 1 3 3 3 0 2 3 2 3 0 AP x y AC y z            n n ，可取 1 ( 3, 1,1) n ． ………………………………………10 分 又平面 PAB 的一个法向量可取 2 (1,0,0)n ． …………………………………………………………11 分 则 1 2 1 2 1 2 3 15cos , | || | 55    n nn n n n ，所以二面角 B AP C  的余弦值为 15 5 ．……………12 分 21.【解析】（1） ( ) 1 2cosf x x   ，令 ( ) 0f x  ，得 1cos 2x  ． ………………………………1 分 故在区间[0, π]上， ( )f x 的唯一零点是 π 3x  ． ……………………………………………………2 分 当 π[0, )3x 时， ( ) 0f x  ， ( )f x 单调递减；当 π( , π]3x 时， ( ) 0f x  ， ( )f x 单调递增．……3 分 故在区间[0, π]上， ( )f x 的极小值为 π π( ) 1 33 3f    ． …………………………………………4 分 当 πx  时， π( ) 1 π 2 π 1 ( )3f x f      ，所以 ( )f x 的最小值为 π π( ) 1 33 3f    ．………5 分 （2）要证： 0x  时， 2( ) e xf x  ，即证： 0x  时， 2( ) (1 2sin )e 1xg x x x    ．…………6 分 2 2 2( ) 2(1 2sin )e (1 2cos )e (3 2 4sin 2cos )ex x xg x x x x x x x          ，……………………7 分 令 ( ) sin , 0h x x x x   ，则 ( ) 1 cos 0h x x    ，即 ( )h x 是 (0, ) 上的增函数． 理科数学参考答案与评分标准 第 4页（共 4页） ∴ ( ) (0) 0h x h  ，即 sinx x ． ……………………………………………………………………9 分 ∴ π3 2 4sin 2cos 3 2sin 4sin 2cos 3 2(sin cos ) 3 2 2 sin( ) 04x x x x x x x x x              ∴ 2( ) (3 2 4sin 2cos )e 0xg x x x x      ．…………………………………………………………11 分 即 ( )g x 是 (0, ) 上的增函数， ( ) (0) 1g x g  ，故当 0x  时， 2( ) e xf x  ． ………………12 分 22．【解析】（1）由 4y m ，得 4 ym  ，代入 24x m ，得 2 4 yx  ，即 2 4y x ．………………2 分 ∴C 的普通方程为 2 4y x ，表示开口向右，焦点为 (1,0)F 的抛物线． ……………………………4 分 （2）设直线 1l 的倾斜角为 ，直线 2l 的倾斜角为 π  ， 则直线 1l 的参数方程为 0 0 cos (sin x x t ty y t        为参数 ) ． …………………………………………………5 分 与 2 4y x 联立得 2 2 2 0 0 0sin (2 sin 4cos ) 4 0t y t y x       ．…………………………………6 分 设方程的两个解为 1 2,t t ，则 2 0 0 1 2 2 4 sin y xt t   ．……………………………………………………………7 分 ∴ 2 0 0 1 2 2 4 sin y xPA PB t t      ． ……………………………………………………………………8 分 则 2 2 0 0 0 0 2 2 4 4 sin (π ) sin y x y xPM PN       ． ……………………………………………………………9 分 ∴ PA PB PM PN   ．………………………………………………………………………………10 分 23.【解析】（1） ( ) 1 2f a a   ，得 2 1 2a    ． ………………………………………………2 分 即 1 3a   ，∴ a 的取值范围是 ( 1,3) ．………………………………………………………………4 分 （2）当 1a  时，函数 ( )f x 在区间[ , ]a a k 上单调递增．……………………………………………5 分 则 min[ ( )] ( ) 1 1f x f a a    ，得 2a  ． max[ ( )] ( ) 2 1 3f x f a k a k      ，得 1k  ．……6 分 当 1a  时， 2 1, 1 ( ) 1 , 1 2 1, x a x f x a a x x a x a            ．…………………………………………………………………8 分 则 min[ ( )] ( ) 1 1f x f a a    ，得 0a  ． max[ ( )] ( ) 2 1 3f x f a k a k      ，得 2k  ．……9 分 综上所述， k 的值为1或 2 ． ………………………………………………………………………………10 分