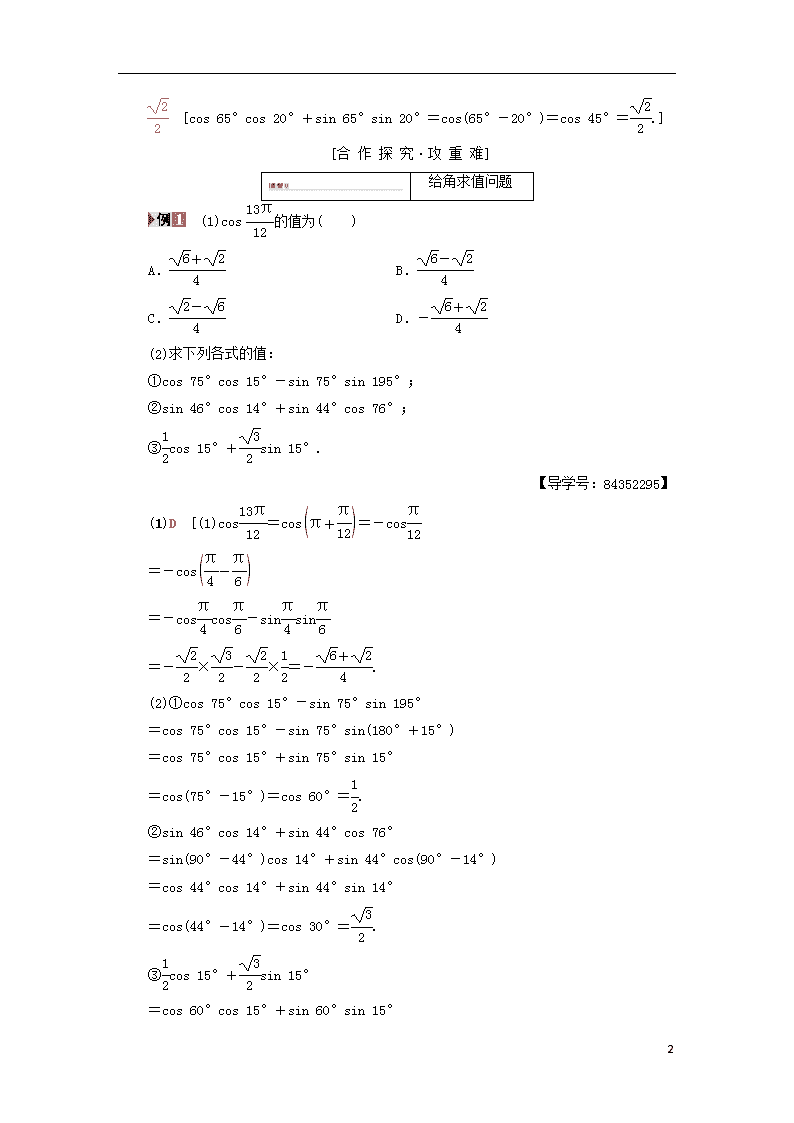2020高中数学 第三章两角差的余弦公式 8页

‎3.1.1　‎两角差的余弦公式 学习目标：1.了解两角差的余弦公式的推导过程．(重点)2.理解用向量法导出公式的主要步骤．(难点)3.熟记两角差的余弦公式的形式及符号特征，并能利用该公式进行求值、计算．(重点、易混点)‎ ‎[自 主 预 习·探 新 知]‎ 两角差的余弦公式 公式 cos(α－β)＝cos_αcos_β＋sin_αsin_β 适用条件 公式中的角α，β都是任意角 公式结构 公式右端的两部分为同名三角函数积，连接符号与左边角的连接符号相反 ‎[基础自测]‎ ‎1．思考辨析 ‎(1)cos(60°－30°)＝cos 60°－cos 30°.(　　)‎ ‎(2)对于任意实数α，β，cos(α－β)＝cos α－cos β都不成立．(　　)‎ ‎(3)对任意α，β∈R，cos(α－β)＝cos αcos β＋sin αsin β都成立．(　　)‎ ‎(4)cos 30°cos 120°＋sin 30°sin 120°＝0.(　　)‎ ‎[解析]　(1)错误．cos(60°－30°)＝cos 30°≠cos 60°－cos 30°.‎ ‎(2)错误．当α＝－45°，β＝45°时，cos(α－β)＝cos(－45°‎ ‎－45°)＝cos(－90°)＝0，cos α－cos β＝cos(－45°)－cos 45°＝0，此时cos(α－β)＝cos α－cos β.‎ ‎(3)正确．结论为两角差的余弦公式．‎ ‎(4)正确．cos 30°cos 120°＋sin 30°sin 120°＝cos(120°－30°)＝cos 90°＝0.‎ ‎[答案]　(1)×　(2)×　(3)√　(4)√‎ ‎2．cos(－15°)的值是(　　)‎ A.　　　　　　　　 B. C. D. D　[cos(－15°)＝cos 15°＝cos(45°－30°)＝cos 45°cos 30°＋sin 45°sin 30°＝×＋×＝.]‎ ‎3．cos 65°cos 20°＋sin 65°sin 20°＝________.‎ 　[cos 65°cos 20°＋sin 65°sin 20°＝cos(65°－20°)＝cos 45°＝.]‎ 8‎ ‎[合 作 探 究·攻 重 难]‎ 给角求值问题 ‎　(1)cos的值为(　　)‎ A．　　　　　　　 B． C． D．－ ‎(2)求下列各式的值：‎ ‎①cos 75°cos 15°－sin 75°sin 195°；‎ ‎②sin 46°cos 14°＋sin 44°cos 76°；‎ ‎③cos 15°＋sin 15°. ‎ ‎【导学号：84352295】‎ ‎(1)D　[(1)cos＝cos＝－cos ‎＝－cos ‎＝－coscos－sinsin ‎＝－×－×＝－.‎ ‎(2)①cos 75°cos 15°－sin 75°sin 195°‎ ‎＝cos 75°cos 15°－sin 75°sin(180°＋15°)‎ ‎＝cos 75°cos 15°＋sin 75°sin 15°‎ ‎＝cos(75°－15°)＝cos 60°＝.‎ ‎②sin 46°cos 14°＋sin 44°cos 76°‎ ‎＝sin(90°－44°)cos 14°＋sin 44°cos(90°－14°)‎ ‎＝cos 44°cos 14°＋sin 44°sin 14°‎ ‎＝cos(44°－14°)＝cos 30°＝.‎ ‎③cos 15°＋sin 15°‎ ‎＝cos 60°cos 15°＋sin 60°sin 15°‎ ‎＝cos(60°－15°)＝cos 45°＝.]‎ ‎[规律方法]　1.解含非特殊角的三角函数式的求值问题的一般思路是：‎ 8‎ ‎(1)把非特殊角转化为特殊角的和或差，正用公式直接求值．‎ ‎(2)在转化过程中，充分利用诱导公式，构造两角差的余弦公式的结构形式，然后逆用公式求值．‎ ‎2．两角差的余弦公式的结构特点：‎ ‎(1)同名函数相乘：即两角余弦乘余弦，正弦乘正弦．‎ ‎(2)把所得的积相加．‎ ‎[跟踪训练]‎ ‎1．化简下列各式：‎ ‎(1)cos(θ＋21°)cos(θ－24°)＋sin(θ＋21°)sin(θ－24°)；‎ ‎(2)－sin 167°·sin 223°＋sin 257°·sin 313°.‎ ‎[解]　(1)原式＝cos[θ＋21°－(θ－24°)]‎ ‎＝cos 45°＝.‎ ‎(2)原式＝－sin(180°－13°)sin(180°＋43°)＋sin(180°＋77°)·sin(360°－47°)‎ ‎＝sin 13°sin 43°＋sin 77°sin 47°‎ ‎＝sin 13°sin 43°＋cos 13°cos 43°‎ ‎＝cos(13°－43°)＝cos(－30°)＝.‎ 给值(式)求值问题 ‎[探究问题]‎ ‎1．若已知α＋β和β的三角函数值，如何求cos α的值？‎ 提示：cos α＝cos[(α＋β)－β]‎ ‎＝cos(α＋β)cos β＋sin(α＋β)sin β.‎ ‎2．利用α－(α－β)＝β可得cos β等于什么？‎ 提示：cos β＝cos[α－(α－β)]＝cos αcos(α－β)＋sin αsin(α－β)．‎ ‎　(1)已知sin α－sin β＝1－，cos α－cos β＝，则cos(α－β)＝(　　)‎ A．－ B．－ C． D． ‎(2)已知sin＝，α∈，求cos α的值. ‎ ‎【导学号：84352296】‎ ‎[思路探究]　(1)先将已知两式平方，再将所得两式相加，结合平方关系和公式C(α－β)‎ 8‎ 求cos(α－β)．‎ ‎(2)由已知角＋α与所求角α的关系即α＝－寻找解题思路．‎ ‎(1)D　[(1)因为sin α－sin β＝1－，‎ 所以sin2α－2sin αsin β＋sin2β＝2，　①‎ 因为cos α－cos β＝，所以cos2α－2cos αcos β＋cos2β＝2，　②‎ ‎①，②两式相加得1－2cos(α－β)＋1＝1－＋＋ 所以－2cos(α－β)＝－ 所以cos(α－β)＝.‎ ‎(2)∵α∈，‎ ‎∴＋α∈，‎ ‎∴cos＝－ ‎＝－＝－.‎ ‎∵α＝－，‎ cos α＝cos ‎＝coscos＋sinsin＝－×＋×＝.]‎ 母题探究：1.将例2(2)的条件改为“sin＝，且<α<”，如何解答？‎ ‎[解]　∵sin＝，且<α<，‎ ‎∴<α＋<π，‎ ‎∴cos＝－＝－，‎ ‎∴cos α＝cos 8‎ ‎＝coscos ＋sinsin ‎＝－×＋×＝.‎ ‎2．将例2(2)的条件改为“sin＝－，α∈”，求cos的值．‎ ‎[解]　∵＜α＜，∴－＜－α＜，‎ 又sin＝－＜0，‎ ‎∴－＜－α＜0，cos＝＝，‎ ‎∴cos＝cos＝cos＝cos＋sin＝×＋×＝－.‎ ‎[规律方法]　给值求值问题的解题策略 (1)已知某些角的三角函数值，求另外一些角的三角函数值时，要注意观察已知角与所求表达式中角的关系，即拆角与凑角.‎ (2)由于和、差角与单角是相对的，因此解题过程中可以根据需要灵活地进行拆角或凑角.常见角的变换有：‎ ‎①α＝(α－β)＋β；‎ ‎②α＝＋；‎ ‎③2α＝(α＋β)＋(α－β)；‎ ‎④2β＝(α＋β)－(α－β).‎ 给值求角问题 ‎　已知sin(π－α)＝，cos(α－β)＝，0＜β＜α＜，求角β的大小.‎ ‎ 【导学号：84352297】‎ ‎[思路探究]　→ ‎→ ‎[解]　因为sin(π－α)＝，‎ 所以sin α＝.因为0＜α＜，‎ 8‎ 所以cos α＝＝.‎ 因为cos(α－β)＝，‎ 且0＜β＜α＜，所以0＜α－β＜，‎ 所以sin(α－β)＝＝，‎ 所以cos β＝cos[α－(α－β)]＝cos αcos(α－β)＋sin αsin(α－β)＝×＋×＝.因为0＜β＜，所以β＝.‎ ‎[规律方法]　已知三角函数值求角的解题步骤 (1)界定角的范围，根据条件确定所求角的范围.‎ (2)求所求角的某种三角函数值.为防止增解最好选取在范围内单调的三角函数.‎ (3)结合三角函数值及角的范围求角.‎ 提醒：在根据三角函数值求角时，易忽视角的范围，而得到错误答案.‎ ‎[跟踪训练]‎ ‎2．已知α，β均为锐角，且cos α＝，cos β＝，求α－β的值．‎ ‎[解]　∵α，β均为锐角，‎ ‎∴sin α＝，sin β＝，‎ ‎∴cos(α－β)＝cos αcos β＋sin αsin β ‎＝×＋×＝.‎ 又sin α