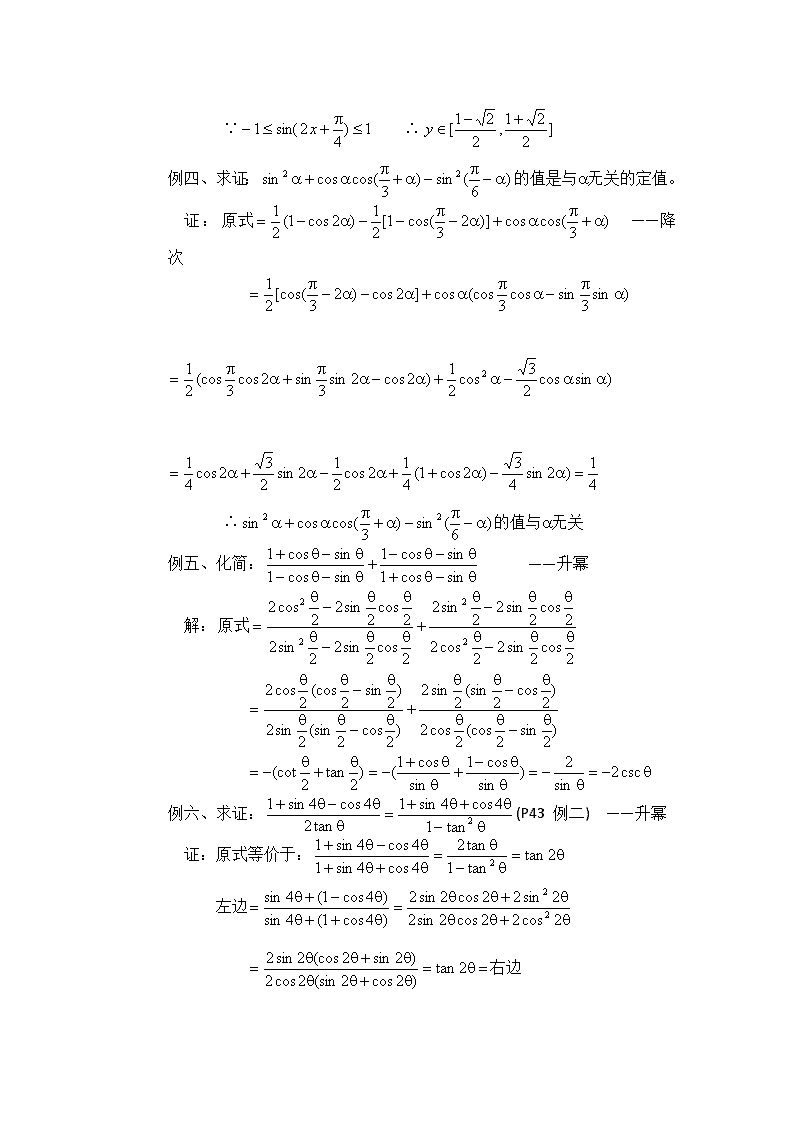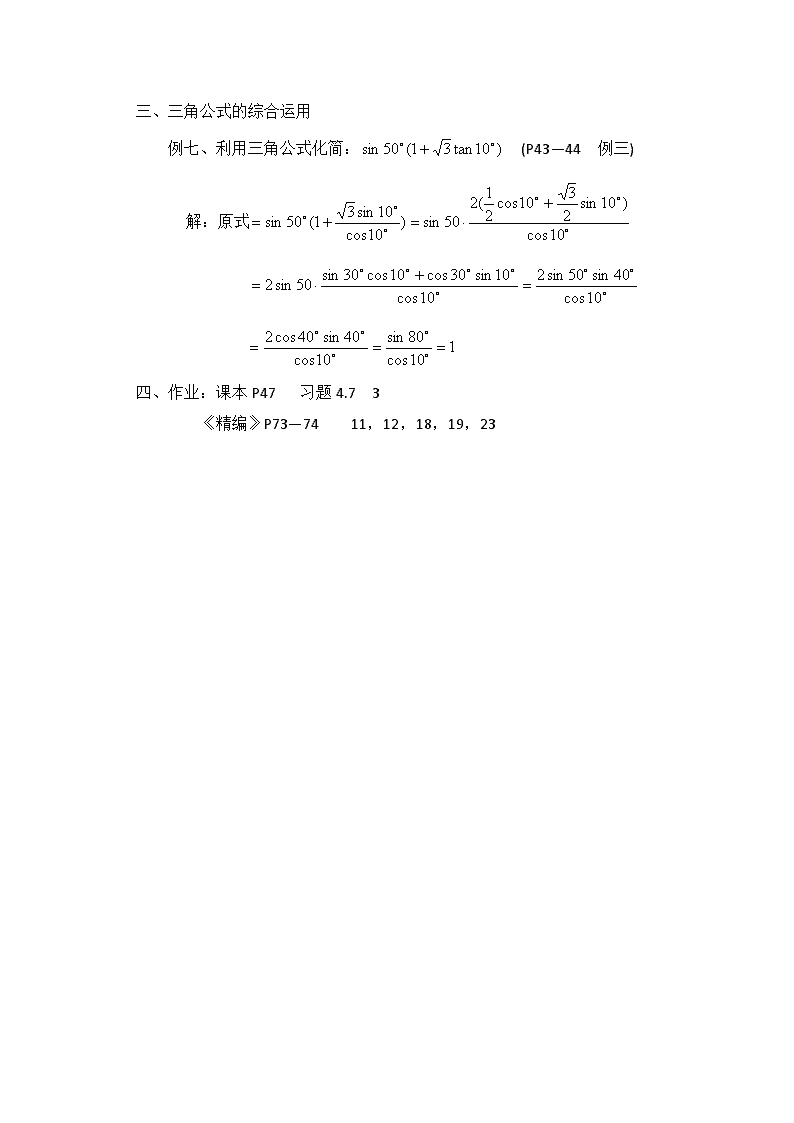【数学】2018届一轮复习苏教版二倍角公式的应用教案 4页

第二十二教时 教材：二倍角公式的应用 ‎ 目的：要求学生能较熟练地运用公式进行化简、求值、证明，增强学生灵活运用数学知识和逻辑推理能力。‎ 过程：‎ 一、 复习公式：‎ 例一、（板演或提问）化简下列各式：‎ ‎1． 2．‎ ‎3．2sin2157.5° - 1 = ‎ ‎4．‎ ‎5．cos20°cos40°cos80° = ‎ ‎ 来源:学§科§网]‎ 例二、求证：[sinq(1+sinq)+cosq(1+cosq)]×[sinq(1-sinq)+cosq(1-cosq)] = sin2q ‎ 证：左边 = (sinq+sin2q+cosq+cos2q)×(sinq-sin2q+cosq-cos2q) ‎ ‎ = (sinq+ cosq+1)×(sinq+cosq -1)‎ ‎ = (sinq+ cosq)2 -1 = 2sinqcosq = sin2q = 右边 ‎ ‎ ∴原式得证 二、 关于“升幂”“降次”的应用 注意：在二倍角公式中，“升次”“降次”与角的变化是相对的。在解题中应视题目的具体情况灵活掌握应用。（以下四个例题可视情况酌情选用）‎ 例三、求函数的值域。（《教学与测试》P115例一）‎ ‎ 解： ——降次 ‎ ∵ ∴[来源: http://wx.jtyjy.com/]‎ 例四、求证：的值是与a无关的定值。‎ ‎ 证： ——降次 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ∴的值与a无关 例五、化简： ——升幂 ‎ 解：‎ ‎ ‎ ‎ ‎ 例六、求证：(P43 例二) ——升幂 ‎ 证：原式等价于：‎ ‎ 左边 ‎ 右边 二、 三角公式的综合运用 例七、利用三角公式化简： (P43—44 例三)‎ ‎ 解：原式 ‎ [来源: http://wx.jtyjy.com/]‎ ‎ [来源:金太阳新课标资源网 HTTP://WX.JTYJY.COM/]‎ 三、 作业：课本P47 习题4.7 3‎ ‎ 《精编》P73—74 11，12，18，19，23[来源:金太阳新课标资源网 HTTP://WX.JTYJY.COM/]‎ ‎ ‎