高中数学必修2教案：2_2_3平面与平面平行的性质 5页

第三课时 平面与平面平行的性质 一、教学目标：‎ ‎1、知识与技能 掌握两个平面平行的性质定理及其应用 ‎2、过程与方法 学生通过观察与类比，借助实物模型理解及其应用 ‎3、情感、态度与价值观 ‎（1）进一步提高学生空间想象能力、思维能力；‎ ‎（2）进一步体会类比的作用；‎ ‎（3）进一步渗透等价转化的思想。‎ 二、教学重点、难点 重点：平面与平面平等的性质定理 难点：平面与平面平等的运用 三、教学方法 讲录结合 教学过程 教学内容 师生互动 设计意图 新课导入 ‎1．直线和平面平行的性质 ‎2．平面和平面平行的性质 ‎3．线线平等线面平行→面面平行 师生共同复习. 教师点出主题.‎ 复习巩固 探索新知 平面和平面平行的性质 ‎1．思考：（1）两个平面平行，那么其中一个平面内的直线与另一个面具有什么关系？‎ ‎（2）两个平面平行，其中一个平面内的直线与另一个平面内的直线具有什么关系？‎ ‎（2）两个平面平行，其中一个平面内的直线与另一平面内的直线在什么条件下不平行？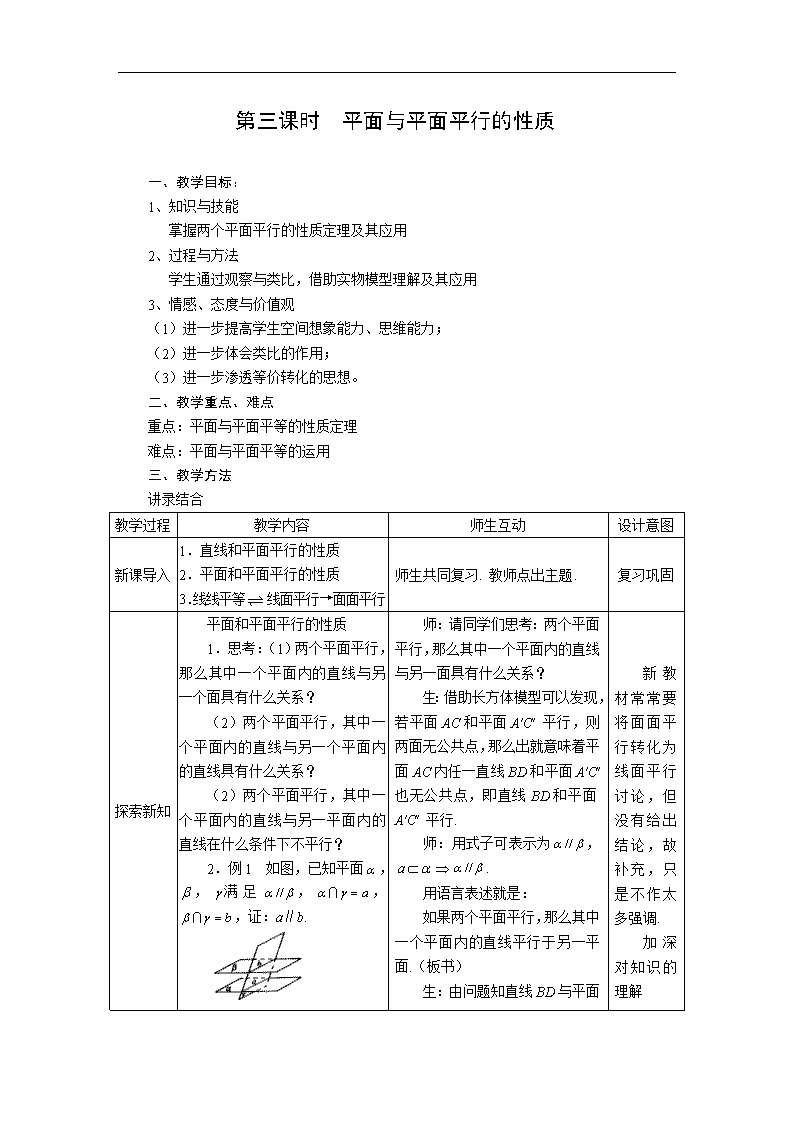‎ ‎2．例1 如图，已知平面，，满足，，，证：a∥b. ‎ 师：请同学们思考：两个平面平行，那么其中一个平面内的直线与另一面具有什么关系？‎ 生：借助长方体模型可以发现，若平面AC和平面A′C′ 平行，则两面无公共点，那么出就意味着平面AC内任一直线BD和平面A′C′ 也无公共点，即直线BD和平面A′C′ 平行.‎ 师：用式子可表示为，.‎ 用语言表述就是：‎ 如果两个平面平行，那么其中一个平面内的直线平行于另一平面.（板书）‎ 生：由问题知直线BD与平面 新教材常常要将面面平行转化为线面平行讨论，但没有给出结论，故补充，只是不作太多强调.‎ ‎ 加深对知识的理解 证明：因为，‎ ‎，‎ 所以，.‎ 又因为，‎ 所以a、b没有公共点，‎ 又因为a、b同在平面内，‎ 所以a∥b.‎ ‎3．定理 如果两个平行平面同时和第三个平面相交，那么它们的交线平行.‎ 上述定理告诉我们，可以由平面与平面平行得出直线与直线平行.‎ A′C′ 平行. BD与平面A′C′ 没有公共点. 也就是说，BD 与平面A′C′ 内的所有直线没有公共点. 因此，直线BD 与平面A′C′ 内的所有直线要么是异面直线，要么是平行直线.‎ 生：由问题2知要两条直线平行，只要他们共面即可.‎ 师：我们把刚才这个结论用符号表示，即是例5的证明.‎ 师生共同完成并得出性质定理.‎ 师引导学生得出结论：两个平行平面的判定定理与性质定理的作用，要害都集中在“平行”二字上，判定定理解决的问题是：在什么样的条件下两个平面平行.性质定理说明的问题是：在什么样的条件下两条直线平行，前者给出了判定两个平面平行的一种方法，后者给出了判定两条直线平行的一种方法.‎ 师下面以例题说明性质定理在解决问题时作用.‎ 典例分析 例2 夹在两个平行平面间的平行线段相等，如图∥，AB∥CD，且A∈，C∈，B∈，D∈，求证：AB = CD.‎ 证明：如图，AB∥CD，AB、CD确定一个平面 ‎，‎ 例3如图，已知平面，AB、CD是异面直线，且AB分别交 师投影例2并读题，学生写出已知求证并作图（师投影）师生共同讨论，边分析边板书.‎ 师：要证两线段相等，已知给的条件又是平行关系，那么证两线段所在四边形是平行四边形，进而说明两线段相等是解决问题常选用的一条途径.‎ 师投影例3并读题 分析：满足怎样的条件的直线与平面平行（线线平行或面面平），我们能在平面内找到一条直线与MN平行吗？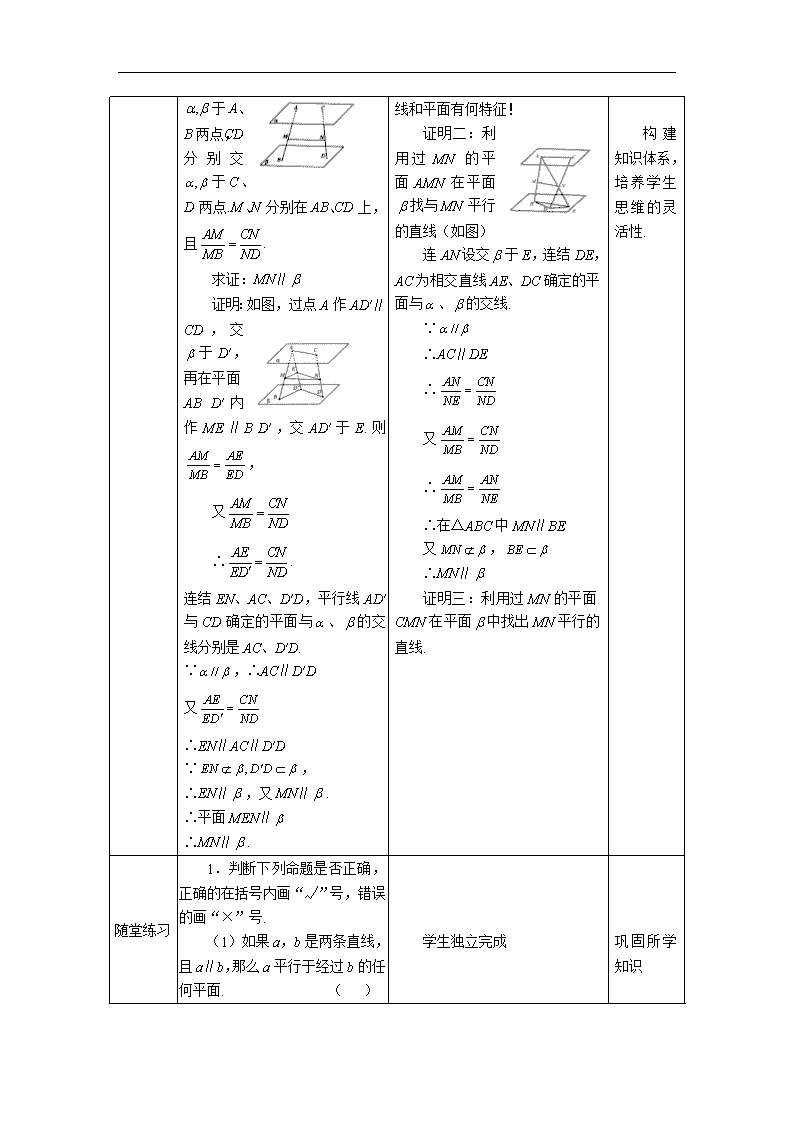能找一个过MN且与 巩固所学知识，培养学生书写表达能力和分析问题解决问题的能力.‎ 于A、B两点，CD分别交于C、D两点.M、N分别在AB、CD上，且.‎ 求证：MN∥‎ 证明：如图，过点A作AD′∥CD，交于D′，再在平面AB D′内作ME∥B D′，交AD′于E.则， ‎ 又 ‎∴.‎ 连结EN、AC、D′D，平行线AD′与CD确定的平面与、的交线分别是AC、D′D.‎ ‎∵，∴AC∥D′D 又 ‎∴EN∥AC∥D′D ‎∵，‎ ‎∴EN∥，又MN∥.‎ ‎∴平面MEN∥‎ ‎∴MN∥.‎ 平行的平面吗？这样的直线和平面有何特征！‎ 证明二：利用过MN的平面AMN在平面找与MN平行的直线（如图）‎ 连AN设交于E，连结DE，AC为相交直线AE、DC确定的平面与、的交线.‎ ‎∵‎ ‎∴AC∥DE ‎∴‎ 又 ‎∴‎ ‎∴在△ABC中MN∥BE 又，‎ ‎∴MN∥‎ 证明三：利用过MN的平面CMN在平面中找出MN平行的直线.‎ 构建知识体系，培养学生思维的灵活性.‎ 随堂练习 ‎1．判断下列命题是否正确，正确的在括号内画“√”号，错误的画“×”号.‎ ‎（1）如果a，b是两条直线，且a∥b，那么a平行于经过b的任何平面. （ ）‎ 学生独立完成 巩固所学知识 ‎（2）如果直线a和平面满足a∥，那么a与内的任何直线平行. （ ）‎ ‎（3）如果直线a，b和平面满足a∥，b∥，那么a∥b.‎ ‎（ ）‎ ‎（4）如果直线a，b和平面满足a∥b，a∥，，那么b∥. （ ）‎ ‎2．如图，正方体ABCD – A′B′C′D′中，AE = A1E1，AF =A1F1，求证EF∥E1F1，且EF = E1F1.‎ 参考答案：‎ 1. ‎（1）×（2）×‎ ‎（3）×（4）√‎ 2. 提示:连结E E1， FF1，证明四边形EFF1E1为平行四边形即可.‎ 归纳总结 ‎1．平面和平面平行的性质 ‎2．线线平行线面平行面面平行 学生先归纳，教师给予补充完善 回顾、反思、归纳知识，提高自我整合知识能力.‎ 课后作业 ‎2.2 第三课时 习案 学生独立完成 固化知识 提升能力 备选例题 例1 如图，设平面a∥平面，AB、CD是两异面直线，M、N分别是AB、CD的中点，且A、C，B、D．求证：MN∥ .‎ ‎【证明】连接BC，取BC的中点E，分别连接ME、NE，‎ 则MN∥AC，∴ME∥平面，‎ 又NE∥BD，∴NE∥，‎ 又ME∩NE = E，∴平面MEN∥平面，‎ ‎∵MN平面MEN．∴MN∥．‎ ‎【评析】要证“面面平面”只要证“线面平面”，要证“线面平行”，只要证“‎ 线线平面”，故问题最终转化为证线与线的平行．‎ 例2 ABCD是矩形，四个顶点在平面内的射影分别为A′、B′、C′、D′，直线A′B′与C′D′不重合，求证：A′B′C′D′是平行四边形．‎ ‎【证明】如图．‎ ‎∵A′、B′、C′、D′分别是A、B、C、D在平面内的射影．‎ ‎∴BB′⊥，CC′⊥，‎ ‎∴BB′∥CC′．‎ ‎≠ ‎ ‎≠‎ ‎∵CC′ 平面CC′D′D，BB′ 平面CC′D′D，‎ ‎∴BB′∥平面CC′D′D.‎ 又∵ABCD是矩形，‎ ‎≠‎ ‎∴AB∥CD，CD 平面CC′D′D，‎ ‎∴AB∥平面CC′D′D ‎∵AB，BB′是平面ABB′A′ 内的两条相交直线，‎ ‎∴平面ABB′A′∥平面CC′D′D．‎ 又∩平面ABB′A′=A′B′，∩平面CC′D′D = C′D′，∴A′B′∥C′D′．‎ 同理，B′C′∥A′D′，∴A′B′C′D′是平行四边形．‎ ‎【评析】在熟知线面平行、面面平行的判定与性质之后，空间平等问题的证明，紧紧抓住“线线平行线面平行面面平行”之间的互相转化而完成证明．‎