【数学】2019届一轮复习北师大版（文科数学）第二章第9讲　函数模型及其应用学案 14页

第9讲　函数模型及其应用 ‎1．几种常见的函数模型 函数模型 函数解析式 一次函数模型 f(x)＝ax＋b(a，b为常数，a≠0)‎ 二次函数模型 f(x)＝ax2＋bx＋c(a，b，c为常数，a≠0)‎ 指数函数模型 f(x)＝bax＋c(a，b，c为常数，a>0且a≠1，b≠0)‎ 对数函数模型 f(x)＝blogax＋c(a，b，c为常数，a>0且a≠1，b≠0)‎ 幂函数模型 f(x)＝axn＋b(a，b，n为常数，a≠0，n≠0)‎ ‎2.三种函数模型性质比较 y＝ax(a>1)‎ y＝logax(a>1)‎ y＝xn(n>0)‎ 在(0，＋∞)上的单调性 增函数 增函数 增函数 增长速度 越来越快 越来越慢 相对平稳 图象的变化 随x值增大，图象与y轴接近平行 随x值增大，图象与x轴接近平行 随n值变化而不同 ‎ 判断正误(正确的打“√”，错误的打“×”)‎ ‎(1)幂函数增长比直线增长更快．(　　)‎ ‎(2)不存在x0，使ax01)的增长速度会超过并远远大于y＝xa(a>1)的增长速度．(　　)‎ ‎(4)“指数爆炸”是指数型函数y＝a·bx＋c(a≠0，b>0，b≠1)增长速度越来越快的形象比喻．(　　)‎ 答案：(1)×　(2)×　(3)√　(4)×‎ ‎ 下列函数中，随x的增大，y的增长速度最快的是(　　)‎ A．y＝ex　　　　　　 B．y＝100 ln x C．y＝x100 D．y＝100·2x 答案：A ‎ (教材习题改编)一根蜡烛长20 cm，点燃后每小时燃烧5 cm，燃烧时剩下的高度h(cm)与燃烧时间t(h)的函数关系用图象表示为图中的(　　)‎ 答案：B ‎ 甲、乙两人在一次赛跑中，从同一地点出发，路程S与时间t的函数关系如图所示，则下列说法正确的是(　　)‎ A．甲比乙先出发 B．乙比甲跑的路程多 C．甲、乙两人的速度相同 D．甲比乙先到达终点 答案：D ‎ (教材习题改编)某公司为了业务发展制定了一个激励销售人员的奖励方案，在销售额x为8万元时，奖励1万元．销售额x为64万元时，奖励4万元．若公司拟定的奖励模型为y＝alog4x＋b.某业务员要得到8万元奖励，则他的销售额应为________万元．‎ 解析：依题意得，‎ 即解得a＝2，b＝－2.‎ 所以y＝2log4x－2，当y＝8时，即2log4x－2＝8.‎ x＝1 024(万元)．‎ 答案：1 024‎ ‎ 据调查，某自行车存车处在某星期日的存车量为4 000辆次，其中变速车存车费是每辆一次0.3元，普通车存车费是每辆一次0.2元．若普通车存车量为x辆次，存车费总收入为y元，则y关于x的函数关系式是________．‎ 解析：由题意知，y＝0.2x＋0.3(4 000－x)＝－0.1x＋1 200，其中x∈[0，4 000]，x∈N.‎ 答案：y＝－0.1x＋1 200，x∈[0，4 000]，x∈N 函数模型的选择 ‎[典例引领]‎ ‎ (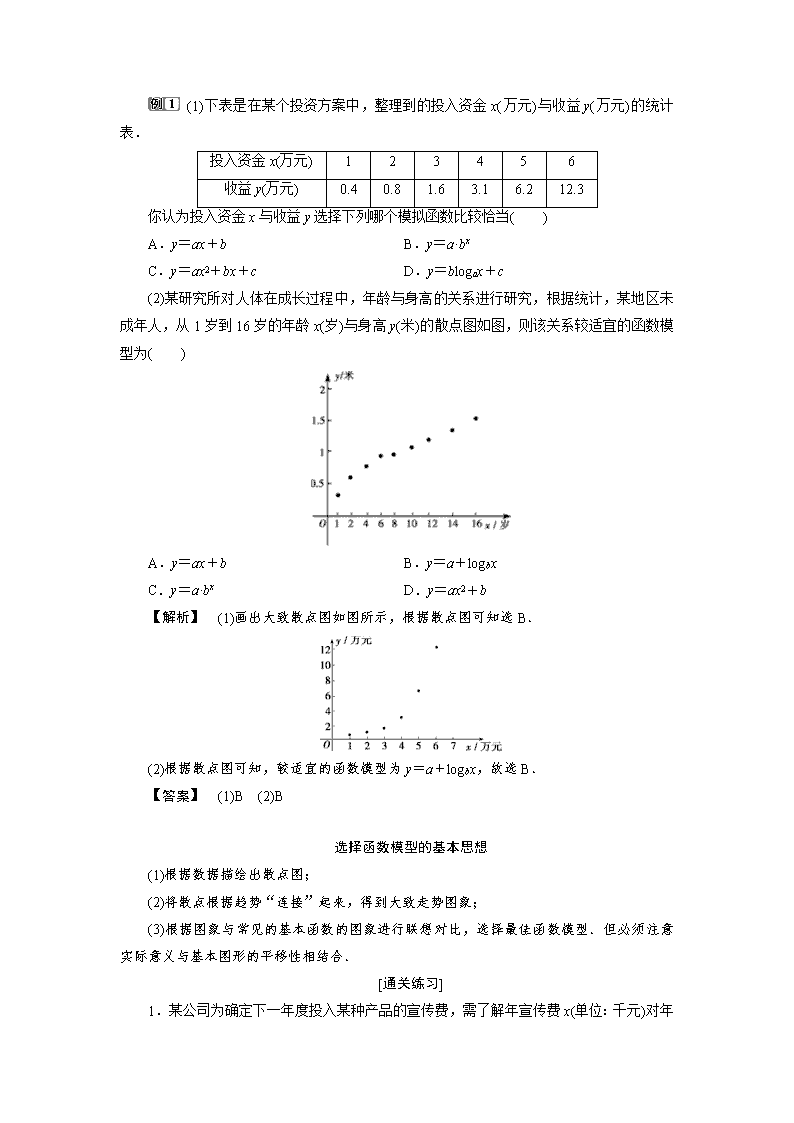1)下表是在某个投资方案中，整理到的投入资金x(万元)与收益y(万元)的统计表．‎ 投入资金x(万元)‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 收益y(万元)‎ ‎0.4‎ ‎0.8‎ ‎1.6‎ ‎3.1‎ ‎6.2‎ ‎12.3‎ 你认为投入资金x与收益y选择下列哪个模拟函数比较恰当(　　)‎ A．y＝ax＋b　　　　　　 B．y＝a·bx C．y＝ax2＋bx＋c D．y＝blogax＋c ‎(2)某研究所对人体在成长过程中，年龄与身高的关系进行研究，根据统计，某地区未成年人，从1岁到16岁的年龄x(岁)与身高y(米)的散点图如图，则该关系较适宜的函数模型为(　　)‎ A．y＝ax＋b B．y＝a＋logbx C．y＝a·bx D．y＝ax2＋b ‎【解析】　(1)画出大致散点图如图所示，根据散点图可知选B．‎ ‎(2)根据散点图可知，较适宜的函数模型为y＝a＋logbx，故选B．‎ ‎【答案】　(1)B　(2)B 选择函数模型的基本思想 ‎(1)根据数据描绘出散点图；‎ ‎(2)将散点根据趋势“连接”起来，得到大致走势图象；‎ ‎(3)根据图象与常见的基本函数的图象进行联想对比，选择最佳函数模型．但必须注意实际意义与基本图形的平移性相结合．　 ‎ ‎[通关练习]‎ ‎1．某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x ‎(单位：千元)对年销售量y(单位：t)的影响．根据近8年的年宣传费xi和年销售量yi(i＝1，2，…，8)数据得到下面的散点图．则下列哪个作为年销售量y关于年宣传费x的函数模型最适合(　　)‎ A．y＝ax＋b B．y＝a＋b C．y＝a·bx D．y＝ax2＋bx＋c 解析：选B．根据散点图知，选择y＝a＋b最适合，故选B．‎ ‎2．某地西红柿上市后，通过市场调查，得到西红柿种植成本Q(单位：元/100 kg)与上市时间t(单位：天)的数据如下表：‎ 时间t ‎60‎ ‎100‎ ‎180‎ 种植成本Q ‎116‎ ‎84‎ ‎116‎ 根据上表数据，从下列函数中选取一个函数描述西红柿种植成本Q与上市时间t的变化关系：‎ Q＝at＋b，Q＝at2＋bt＋c，Q＝a·bt，Q＝a·logbt.‎ 利用你选取的函数，求：‎ ‎(1)西红柿种植成本最低时的上市天数是________；‎ ‎(2)最低种植成本是________元/100 kg.‎ 解析：因为随着时间的增加，种植成本先减少后增加，而且当t＝60和t＝180时种植成本相等，再结合题中给出的四种函数关系可知，种植成本与上市时间的变化关系应该用二次函数Q＝at2＋bt＋c，即Q＝a(t－120)2＋m描述，将表中数据代入可得 解得 所以Q＝0.01(t－120)2＋80，故当上市天数为120时，种植成本取到最低值80元/100 kg.‎ 答案：(1)120　(2)80‎ 函数模型的应用 ‎[典例引领]‎ ‎ 已知炮弹发射后的轨迹在方程y＝kx－(1＋k2)x2(k>0)表示的曲线上，其中k与发射方向有关．炮的射程是指炮弹落地点的横坐标．‎ ‎(1)求炮的最大射程；‎ ‎(2)设在第一象限有一飞行物(忽略其大小)，其飞行高度为3.2千米，试问它的横坐标a不超过多少时，炮弹可以击中它？请说明理由．‎ ‎【解】　(1)在y＝kx－(1＋k2)x2(k>0)中，‎ 令y＝0，得kx－(1＋k2)x2＝0.‎ 由实际意义和题设条件知x>0，k>0.‎ 解以上关于x的方程得x＝＝≤＝10，当且仅当k＝1时取等号．‎ 所以炮的最大射程是10千米．‎ ‎(2)因为a>0，所以炮弹可以击中目标⇔存在k>0，使ka－(1＋k2)a2＝3.2成立⇔关于k的方程a2k2－20ak＋a2＋64＝0有正根，‎ 得 解得0200，两边同时取对数，得n－1>，又≈＝3.8，则n>4.8，即a5开始超过200，所以2019年投入的研发资金开始超过200万元，故选B．‎ ‎【答案】　B ‎ 角度三　构建分段函数模型 ‎ 提高过江大桥的车辆通行能力可改善整个城市的交通状况．在一般情况下，大桥上的车流速度v(单位：千米/时)是车流密度x(单位：辆/千米)的函数．当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过20辆/千米时，车流速度为60千米/时．研究表明：当20≤x≤200时，车流速度v是车流密度x的一次函数．‎ ‎(1)当0≤x≤200时，求函数v(x)的表达式；‎ ‎(2)当车流密度x为多大时，车流量(单位时间内通过桥上某观测点的车辆数，单位：辆/时)f(x)＝x·v(x)可以达到最大，并求出最大值．(精确到1辆/时)‎ ‎【解】　(1)由题意，当0≤x≤20时，v(x)＝60；‎ 当20≤x≤200时，设v(x)＝ax＋b，‎ 再由已知得解得 故函数v(x)的表达式为v(x)＝ ‎(2)依题意并由(1)可得f(x)＝ 当0≤x≤20时，f(x)为增函数，故当x＝20时，其最大值为60×20＝1 200；‎ 当200，解得x>2.3.‎ 因为x∈N*，所以3≤x≤6，x∈N*.‎ 当x>6时，y＝[50－3(x－6)]x－115.‎ 令[50－3(x－6)]x－115>0，有3x2－68x＋115<0.‎ 又x∈N*，所以6185，‎ 所以当每辆自行车的日租金定为11元时，才能使一日的净收入最多．‎ ‎6．(2018·辽宁抚顺一模)食品安全问题越来越引起人们的重视，农药、化肥的滥用对人民群众的健康带来一定的危害，为了给消费者带来放心的蔬菜，某农村合作社每年投入200万元，搭建了甲、乙两个无公害蔬菜大棚，每个大棚至少要投入20万元，其中甲大棚种西红柿，乙大棚种黄瓜，根据以往的种菜经验，发现种西红柿的年收入P、种黄瓜的年收入Q与投入a(单位：万元)满足P＝80＋4，Q＝a＋120，设甲大棚的投入为x(单元：万元)，每年两个大棚的总收益为f(x)(单位：万元)．‎ ‎(1)求f(50)的值；‎ ‎(2)试问如何安排甲、乙两个大棚的投入，才能使总收益f(x)最大？‎ 解：(1)由题意知甲大棚投入50万元，‎ 则乙大棚投入150万元，‎ 所以f(50)＝80＋4＋×150＋120＝277.5(万元)．‎ ‎(2)f(x)＝80＋4＋(200－x)＋120＝－x＋4＋250，‎ 依题意得⇒20≤x≤180，‎ 故f(x)＝－x＋4＋250(20≤x≤180)．‎ 令t＝，则t∈[2，6]，y＝－t2＋4t＋250＝－(t－8)2＋282，‎ 当t＝8，即x＝128时，f(x)取得最大值，f(x)max＝282.‎ 所以甲大棚投入128万元，乙大棚投入72万元时，总收益最大，且最大总收益为282万元．‎