全国百强校2021届高三上学期领军考试（9月）试题 数学（文） Word版含解析 12页

www.ks5u.com ‎2020－2021学年上学期全国百强名校 ‎“领军考试”高三数学(文数)‎ ‎2020.9‎ 注意事项：‎ ‎1.答卷前，考生务必将自己的姓名，准考证号填写在本试题相应的位置。‎ ‎2.全部答案在答题卡上完成，答在本试题上无效。‎ ‎3.回答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案用0.5mm黑色笔迹签字笔写在答题卡上。‎ ‎4.考试结束后，将本试题和答题卡一并交回。‎ 一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1.已知集合U＝{x∈Z|0≤x≤6}，A＝{1，3，4}，B＝{l，3，5}，则B∩(A)＝‎ A.{5} B.{7} C.{5，7} D.{5，6}‎ ‎2.已知α是锐角，若cos(α＋)＝，则cos2α＝‎ A. B. C.－ D.－‎ ‎3.已知命题p：x>2，x2>2x，命题q：x0∈R，ln(x02＋1)<0，则 A.命题p∨q是假命题 B.命题p∧q是真命题 C.命题p∨(q)是假命题 D.命题p∧(q)是真命题 ‎4.已知函数f(x)＝ln(＋x)＋x3－2，则f(2020)＋f(－2020)＝‎ A.2 B.0 C.－2 D.－4‎ ‎5.函数f(x)＝sin(2x＋φ)(φ>0)对任意实数x，都有f(x)≤|f()|，则φ的最小值为 A.π B. C. 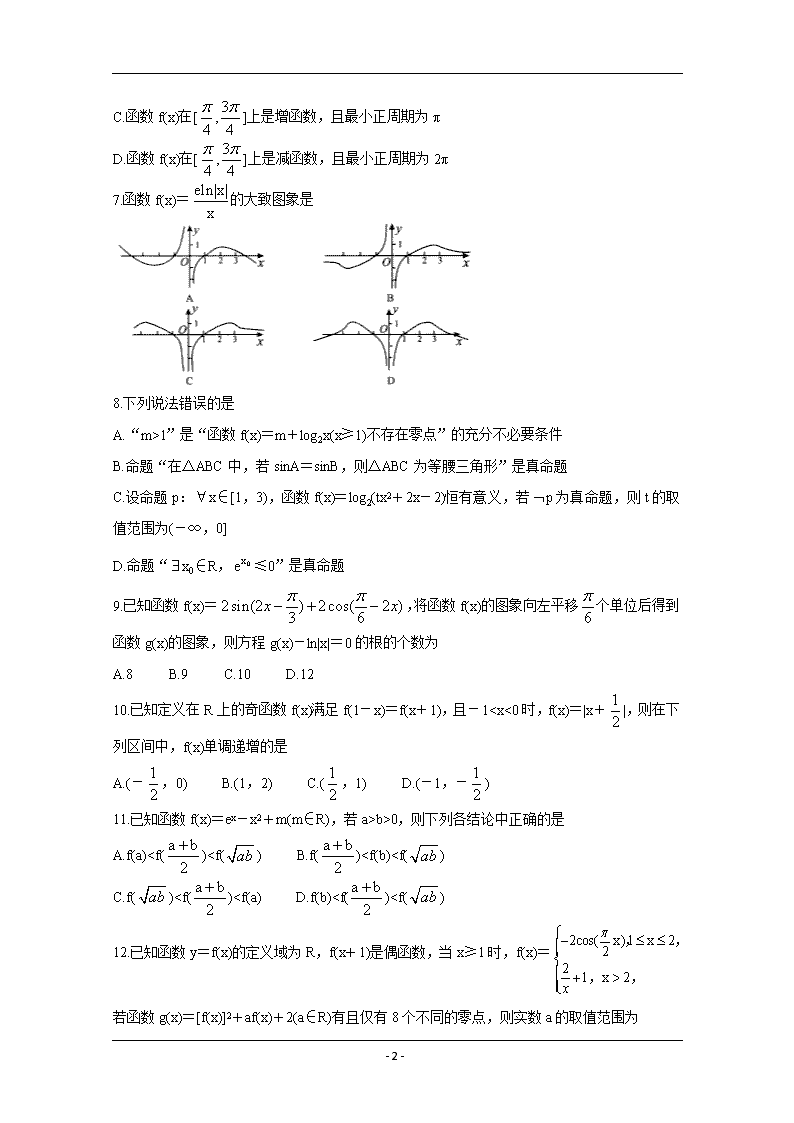D.‎ ‎6.已知函数f(x)＝2sinxcosx－2cos2x＋，那么下列说法正确的是 A.函数f(x)在[]上是增函数，且最小正周期为2π B.函数f(x)在[]上是减函数，且最小正周期为π - 12 -‎ C.函数f(x)在[]上是增函数，且最小正周期为π D.函数f(x)在[]上是减函数，且最小正周期为2π ‎7.函数f(x)＝的大致图象是 ‎8.下列说法错误的是 A.“m>1”是“函数f(x)＝m＋log2x(x≥1)不存在零点”的充分不必要条件 B.命题“在△ABC中，若sinA＝sinB，则△ABC为等腰三角形”是真命题 C.设命题p：x∈[1，3)，函数f(x)＝log2(tx2＋2x－2)恒有意义，若p为真命题，则t的取值范围为(－∞，0]‎ D.命题“x0∈R，≤0”是真命题 ‎9.已知函数f(x)＝，将函数f(x)的图象向左平移个单位后得到函数g(x)的图象，则方程g(x)－ln|x|＝0的根的个数为 A.8 B.9 C.10 D.12‎ ‎10.已知定义在R上的奇函数f(x)满足f(1－x)＝f(x＋1)，且－1b>0，则下列各结论中正确的是 A.f(a)0，如果命题“p∧q”为真命题，求实数a的取值范围。‎ ‎18.(12分)‎ 已知函数f(x)＝ (a>0)。‎ ‎(1)若f(x)在[0，＋∞)上为增函数，求实数a的取值范围；‎ ‎(2)当a＝1时，若x∈[0，＋∞)，使得不等式mf(x)≤e－x－m，求实数m的取值范围。‎ ‎19.(12分)‎ 若当x＝x0时，函数f(x)＝3sinx＋4cosx取得最大值。‎ ‎(1)求cosx0的值；‎ ‎(2)若m是f(x)的一个零点，当m∈(，π)时，求sin(m＋x0)的值。‎ ‎20.(12分)‎ 函数f(x)＝sin(ωx＋φ)(ω>0，0<φ<π)的两个相邻的最低点与最高点分别是(，－1)，(，1)。‎ ‎(1)问当f(x)向左最少平移多少个单位时，得到的函数关于坐标原点对称?‎ ‎(2)求证：对于任意的x∈[－，]，都有f(x)≥－。‎ ‎21.(12分)‎ - 12 -‎ 设函数f(x)＝xlnx，g(x)＝。‎ ‎(1)求g(x)的单调区间；‎ ‎(2)若x1>x2>0时，总有(x12－x22)>f(x1)－f(x2)恒成立，求实数m的取值范围。‎ ‎22.(12分)‎ 已知函数f(x)＝lnx＋－b。‎ ‎(1)若在曲线y＝f(x)上的一点P的切线方程为x轴，求此时b的值；‎ ‎(2)当a<0时，若f(x)≥ax恒成立，求a＋2b的取值范围。‎ - 12 -‎ - 12 -‎ - 12 -‎ - 12 -‎ - 12 -‎ - 12 -‎ - 12 -‎ - 12 -‎ - 12 -‎