【数学】2019届一轮复习北师大版（文科数学）第八章第6讲　平行、垂直的综合问题学案 17页

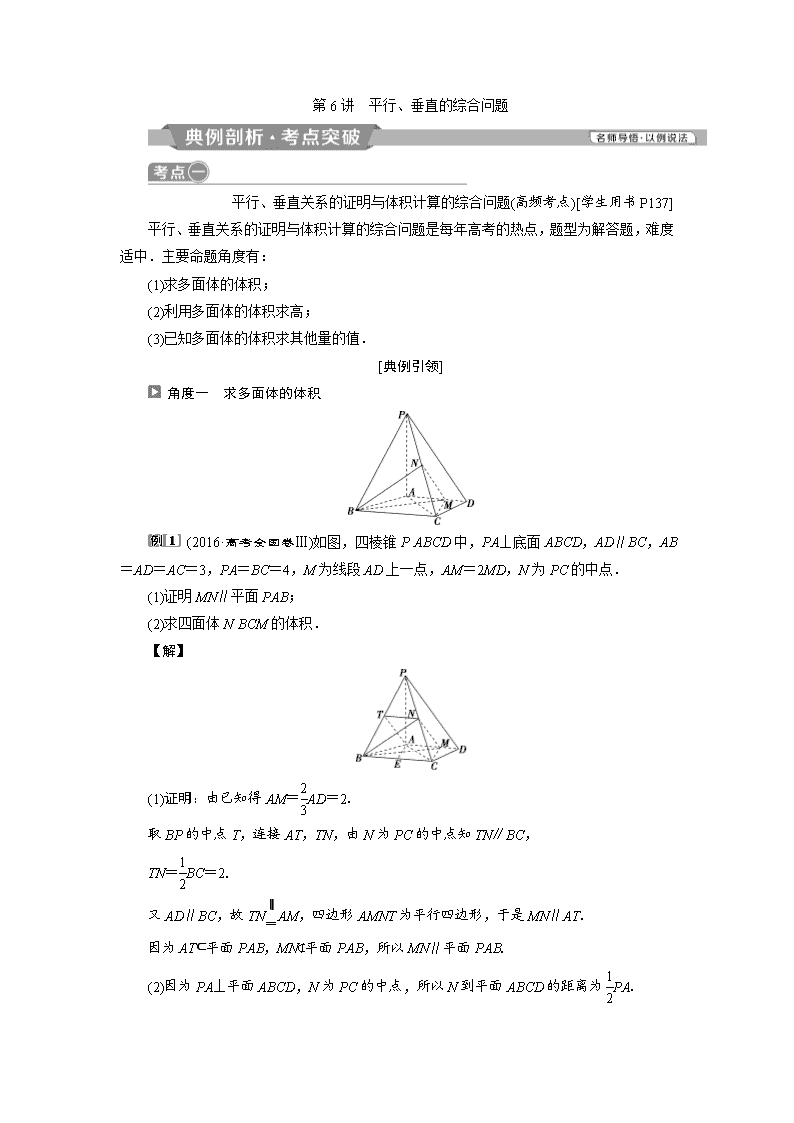
第6讲　平行、垂直的综合问题 ‎　　　　　　平行、垂直关系的证明与体积计算的综合问题(高频考点)[学生用书P137]‎ 平行、垂直关系的证明与体积计算的综合问题是每年高考的热点，题型为解答题，难度适中．主要命题角度有：‎ ‎(1)求多面体的体积；‎ ‎(2)利用多面体的体积求高；‎ ‎(3)已知多面体的体积求其他量的值．‎ ‎[典例引领]‎ ‎ 角度一　求多面体的体积 ‎ (2016·高考全国卷Ⅲ)如图，四棱锥PABCD中，PA⊥底面ABCD，AD∥BC，AB＝AD＝AC＝3，PA＝BC＝4，M为线段AD上一点，AM＝2MD，N为PC的中点．‎ ‎(1)证明MN∥平面PAB；‎ ‎(2)求四面体NBCM的体积．‎ ‎【解】　‎ ‎(1)证明：由已知得AM＝AD＝2.‎ 取BP的中点T，连接AT，TN，由N为PC的中点知TN∥BC，‎ TN＝BC＝2.‎ 又AD∥BC，故TNAM，四边形AMNT为平行四边形，于是MN∥AT.‎ 因为AT⊂平面PAB，MN⊄平面PAB，所以MN∥平面PAB.‎ ‎(2)因为PA⊥平面ABCD，N为PC的中点，所以N到平面ABCD的距离为PA.‎ 取BC的中点E，连接AE，由AB＝AC＝3得AE⊥BC，AE＝＝.‎ 由AM∥BC得M到BC的距离为，故S△BCM＝×4×＝2.‎ 所以四面体NBCM的体积VNBCM＝×S△BCM×＝.‎ ‎ 角度二　利用多面体的体积求高 ‎ 如图，四棱锥PABCD中，底面ABCD为矩形，PA⊥底面ABCD，E为PD的中点．‎ ‎(1)证明：PB∥平面AEC；‎ ‎(2)设AP＝1，AD＝，三棱锥PABD的体积V＝，求A到平面PBC的距离．‎ ‎【解】　‎ ‎(1)证明：如图，设BD与AC的交点为O，连接EO.‎ 因为ABCD为矩形，所以O为BD的中点．‎ 又E为PD的中点，所以EO∥PB.因为EO⊂平面AEC，PB⊄平面AEC，所以PB∥平面AEC.‎ ‎(2)由题意得三棱锥PABD的体积V＝PA·AB·AD＝AB.‎ 由V＝，可得AB＝.作AH⊥PB于H.‎ 由题设知BC⊥平面PAB，所以BC⊥AH，故AH⊥平面PBC.‎ 在Rt△PAB中，由勾股定理可得PB＝，所以AH＝＝.‎ 所以A到平面PBC的距离为.‎ ‎ 角度三　已知多面体的体积求其他量的值 ‎ (2017·高考全国卷Ⅰ)如图，在四棱锥PABCD中，AB∥CD，且∠BAP＝∠CDP＝90°.‎ ‎(1)证明：平面PAB⊥平面PAD；‎ ‎(2)若PA＝PD＝AB＝DC，∠APD＝90°，且四棱锥PABCD的体积为，求该四棱锥的侧面积．‎ ‎【解】　(1)证明：由∠BAP＝∠CDP＝90°，得AB⊥AP，CD⊥PD.由于AB∥CD，故AB⊥PD，从而AB⊥平面PAD.‎ 又AB⊂平面PAB，所以平面PAB⊥平面PAD.‎ ‎(2)‎ 如图所示，在平面PAD内作PE⊥AD，垂足为E.‎ 由(1)知，AB⊥平面PAD，故AB⊥PE，可得PE⊥平面ABCD.‎ 设AB＝x，则由已知可得AD＝x，PE＝x.故四棱锥PABCD的体积VPABCD＝AB·AD·PE＝x3.由题设得x3＝，故x＝2.‎ 从而PA＝PD＝2，AD＝BC＝2，PB＝PC＝2.‎ 可得四棱锥PABCD的侧面积为 PA·PD＋PA·AB＋PD·DC＋BC2sin 60°＝6＋2.‎ ‎(1)几何体的体积 柱体的体积V＝S底·h.‎ 锥体的体积V＝S底·h.‎ ‎(2)几何体的表面积 直棱柱的侧面积S侧＝C底·l，其他几何体一般要对各个侧面、底面逐个分析求解面积，最后求和．‎ ‎(3)计算几何体体积的关键及注意点 计算几何体的体积时，关键是确定几何体的高，若是不方便求，要注意进行体积的转化．　 ‎ ‎[通关练习]‎ 如图，在底面为菱形的四棱锥PABCD中，PA⊥AD，PA⊥CD，E为侧棱PC 上一点．‎ ‎(1)若BE⊥PC，求证：PC⊥平面BDE；‎ ‎(2)若PA∥平面BDE，求平面BDE把四棱锥PABCD分成两部分的体积比．‎ 解：(1)证明：连接AC，因为四边形ABCD为菱形，所以AC⊥BD.‎ 因为PA⊥AD，PA⊥CD，且AD∩CD＝D，‎ 所以PA⊥底面ABCD，所以PA⊥BD.‎ 又PA∩AC＝A，所以BD⊥平面PAC，所以BD⊥PC.‎ 因为BE⊥PC，BD∩BE＝B，所以PC⊥平面BDE.‎ ‎(2)设AC∩BD＝O，连接OE，因为四边形ABCD为菱形，所以AO＝OC.‎ 因为PA∥平面BDE，平面PAC∩平面BDE＝OE，所以PA∥OE，‎ 所以PE＝EC，即E是PC的中点．‎ 由(1)知PA⊥底面ABCD，所以点E到平面ABCD的距离为PA.‎ 故三棱锥EBCD与四棱锥PABCD的体积比值为 ＝＝＝，‎ 所以平面BDE把四棱锥PABCD分成两部分的体积比为1∶3(或3∶1)．‎ ‎　　　　　　平面图形折叠成空间几何体问题 ‎[学生用书P138]‎ ‎[典例引领]‎ ‎ (2016·高考全国卷Ⅱ)如图，菱形ABCD的对角线AC与BD交于点O，点E、F分别在AD，CD上，AE＝CF，EF交BD于点H.将△DEF沿EF折到△D′EF的位置．‎ ‎(1)证明：AC⊥HD′；‎ ‎(2)若AB＝5，AC＝6，AE＝，OD′＝2，求五棱锥D′ABCFE的体积．‎ ‎【解】　(1)证明：由已知得AC⊥BD，AD＝CD.‎ 又由AE＝CF得＝，故AC∥EF.‎ 由此得EF⊥HD，EF⊥HD′，所以AC⊥HD′.‎ ‎(2)由EF∥AC得＝＝.‎ 由AB＝5，AC＝6得DO＝BO＝＝4.‎ 所以OH＝1，D′H＝DH＝3.‎ 于是OD′2＋OH2＝(2)2＋12＝9＝D′H2，‎ 故OD′⊥OH.‎ 由(1)知，AC⊥HD′，‎ 又AC⊥BD，BD∩HD′＝H，‎ 所以AC⊥平面BHD′，‎ 于是AC⊥OD′.‎ 又由OD′⊥OH，AC∩OH＝O，‎ 所以OD′⊥平面ABC.‎ 又由＝得EF＝.‎ 五边形ABCFE的面积S＝×6×8－××3＝.‎ 所以五棱锥D′ABCFE的体积V＝××2＝.‎ 平面图形的翻折问题，关键是搞清翻折前后图形中线面位置关系和度量关系的变化情况．一般地，翻折后还在同一平面上的性质不发生变化，不在同一个平面上的性质发生变化．　 ‎ ‎[通关练习]‎ 如图(1)，在直角梯形ABCD中，AD∥BC，∠BAD＝，AB＝BC＝AD＝a，E是AD的中点，O是AC与BE的交点．将△ABE沿BE折起到图(2)中△A1BE的位置，得到四棱锥A1BCDE.‎ ‎(1)证明：CD⊥平面A1OC；‎ ‎(2)当平面A1BE⊥平面BCDE时，四棱锥A1BCDE的体积为36，求a的值．‎ 解：(1)证明：在题图(1)中，连接EC，‎ 因为AB＝BC＝AD＝a，‎ E是AD的中点，∠BAD＝，所以BE⊥AC.‎ 即在题图(2)中，BE⊥A1O，BE⊥OC，‎ 从而BE⊥平面A1OC.‎ 又CD∥BE，所以CD⊥平面A1OC.‎ ‎(2)由已知，平面A1BE⊥平面BCDE，‎ 且平面A1BE∩平面BCDE＝BE，‎ 又由(1)可得A1O⊥BE，所以A1O⊥平面BCDE.‎ 即A1O是四棱锥A1BCDE的高．‎ 由题图(1)知，A1O＝AO＝AB＝a，平行四边形BCDE的面积S＝BC·AB＝a2，从而四棱锥A1BCDE的体积为V＝S·A1O＝×a2×a＝a3.‎ 由a3＝36，得a＝6.‎ ‎　　　　　　立体几何中的探索性问题 ‎[学生用书P139]‎ ‎[典例引领]‎ ‎ 如图，直三棱柱ABCA1B1C1中，D，E分别是棱BC，AB的中点，点F在棱CC1上，已知AB＝AC，AA1＝3，BC＝CF＝2.‎ ‎(1)求证：C1E∥平面ADF.‎ ‎(2)设点M在棱BB1上，当BM为何值时，平面CAM⊥平面ADF.‎ ‎【解】　(1)证明：连接CE交AD于O，连接OF.‎ 因为CE，AD为△ABC的中线，则O为△ABC的重心，故＝＝，故OF∥C1E，‎ 因为OF⊂平面ADF，C1E⊄平面ADF，‎ 所以C1E∥平面ADF.‎ ‎(2)当BM＝1时，平面CAM⊥平面ADF.‎ 证明如下：因为AB＝AC，‎ 故AD⊥BC.在直三棱柱ABCA1B1C1中，‎ BB1⊥平面ABC，BB1⊂平面B1BCC1，‎ 故平面B1BCC1⊥平面ABC.‎ 又平面B1BCC1∩平面ABC＝BC，所以AD⊥平面B1BCC1，CM⊂平面B1BCC1，故AD⊥CM.‎ 又BM＝1，BC＝2，CD＝1，FC＝2，‎ 故△CBM≌△FCD.‎ 易证CM⊥DF，DF与AD相交，‎ 故CM⊥平面ADF.‎ 又CM⊂平面CAM，‎ 故平面CAM⊥平面ADF.‎ 解决探索性问题的方法 ‎(1)对命题条件的探索的三种途径 途径一：先猜后证，即先观察与尝试给出条件再证明．‎ 途径二：先通过命题成立的必要条件探索出命题成立的条件，再证明充分性．‎ 途径三：将几何问题转化为代数问题，探索出命题成立的条件．‎ ‎(2)对命题结论的探索方法 从条件出发，探索出要求的结论是什么，对于探索结论是否存在，求解时常假设结论存在，再寻找与条件相容或者矛盾的结论．‎ ‎[注意]　对探索性问题应先写出结论，再写出证明过程或理由．　 ‎ ‎[通关练习]‎ ‎1．如图，在直四棱柱ABCDA1B1C1D1中，已知DC＝DD1＝2AD＝2AB，AD⊥DC，AB∥DC.‎ ‎(1)求证：D1C⊥AC1；‎ ‎(2)问在棱CD上是否存在点E，使D1E∥平面A1BD.若存在，确定点E的位置；若不存在，说明理由．‎ 解：(1)证明：‎ 在直四棱柱ABCDA1B1C1D1中，连接C1D，‎ 因为DC＝DD1，所以四边形DCC1D1是正方形，‎ 所以DC1⊥D1C.‎ 又AD⊥DC，AD⊥DD1，DC∩DD1＝D，‎ 所以AD⊥平面DCC1D1，‎ 又D1C⊂平面DCC1D1，‎ 所以AD⊥D1C.‎ 因为AD⊂平面ADC1，DC1⊂平面ADC1，且AD∩DC1＝D，‎ 所以D1C⊥平面ADC1，‎ 又AC1⊂平面ADC1，所以D1C⊥AC1.‎ ‎(2)假设存在点E，‎ 使D1E∥平面A1BD.‎ 连接AD1，AE，D1E，‎ 设AD1∩A1D＝M，BD∩AE＝N，‎ 连接MN，因为平面AD1E∩平面A1BD＝MN，‎ 要使D1E∥平面A1BD，‎ 可使MN∥D1E，‎ 又M是AD1的中点，‎ 则N是AE的中点．‎ 又易知△ABN≌△EDN，‎ 所以AB＝DE.‎ 即E是DC的中点．‎ 综上所述，当E是DC的中点时，可使D1E∥平面A1BD.‎ ‎2．(2018·成都模拟)在四棱锥EABCD中，底面ABCD是正方形，AC与BD交于点O，EC⊥底面ABCD，点F为BE的中点．‎ ‎(1)求证：DE∥平面ACF.‎ ‎(2)若AB＝CE，在线段EO上是否存在点G，使CG⊥平面BDE？若存在，求出的值；若不存在，请说明理由．‎ 解：(1)证明：连接OF，由四边形ABCD是正方形可知，点O为BD的中点．‎ 又F为BE的中点，所以OF∥DE.‎ 又OF⊂平面ACF，DE⊄平面ACF，‎ 所以DE∥平面ACF.‎ ‎(2)存在点G，此时＝.证明如下：‎ 若CG⊥平面BDE，则必有CG⊥OE，于是作CG⊥OE于点G.‎ 因为EC⊥底面ABCD，所以BD⊥EC，‎ 又底面ABCD是正方形，‎ 所以BD⊥AC，又EC∩AC＝C，所以BD⊥平面ACE.‎ 而CG⊂平面ACE，所以CG⊥BD.‎ 又OE∩BD＝O，‎ 所以CG⊥平面BDE.‎ 又AB＝CE，所以CO＝AB＝CE，‎ 所以点G为EO的中点，所以＝.‎ ‎ 空间几何体体积的计算方法 ‎(1)若所给定的几何体是柱体、锥体或台体等规则几何体，则可直接利用公式进行求解．其中，等积转换法多用来求三棱锥的体积．‎ ‎(2)若所给定的几何体是不规则几何体，‎ 则将不规则的几何体通过分割或补形转化为规则几何体，再利用公式求解．‎ ‎(3)若以三视图的形式给出几何体，则应先根据三视图得到几何体的直观图，然后根据条件求解．‎ ‎ 折叠问题的求解策略 ‎(1)关键是搞清折叠前后的变化量和不变量．折线同侧的量位置关系不变，折线两侧的位置关系是变化量．‎ ‎(2)综合考虑折叠前后的图形，既要分析折叠后的图形，也要分析折叠前的图形，进而将其转化为立体几何的常规问题求解．‎ ‎ 存在性问题的求解策略 对于线面关系中的存在性问题，首先假设存在，然后在该假设条件下，利用线面关系的相关定理、性质进行推理论证，寻找假设满足的条件，若满足则肯定假设，若得出矛盾的结论则否定假设．　‎ ‎ ‎ ‎[学生用书P307(单独成册)]‎ ‎1.‎ 如图，边长为a的等边三角形ABC的中线AF与中位线DE交于点G，已知△A′DE是△ADE绕DE旋转过程中的一个图形，则下列命题中正确的是(　　)‎ ‎①动点A′在平面ABC上的射影在线段AF上；‎ ‎②BC∥平面A′DE；‎ ‎③三棱锥A′FED的体积有最大值．‎ A．①　　　　　　　　 B.①②‎ C．①②③ D．②③‎ 解析：选C.①中由已知可得平面A′FG⊥平面ABC，‎ 所以点A′在平面ABC上的射影在线段AF上．‎ ‎②BC∥DE，根据线面平行的判定定理可得BC∥平面A′DE.‎ ‎③当平面A′DE⊥平面ABC时，三棱锥A′FED的体积达到最大，故选C.‎ ‎2．如图所示，四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°.将△ADB沿BD折起，使平面ABD⊥平面BCD，构成三棱锥ABCD，则在三棱锥ABCD 中，下列结论正确的是(　　)‎ A．平面ABD⊥平面ABC B．平面ADC⊥平面BDC C．平面ABC⊥平面BDC D．平面ADC⊥平面ABC 解析：选D.因为在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°，‎ 所以BD⊥CD.‎ 又平面ABD⊥平面BCD，‎ 且平面ABD∩平面BCD＝BD，‎ 故CD⊥平面ABD，则CD⊥AB.‎ 又AD⊥AB，AD∩CD＝D，AD⊂平面ADC，CD⊂平面ADC，故AB⊥平面ADC.‎ 又AB⊂平面ABC，所以平面ADC⊥平面ABC.‎ ‎3．如图，四边形ABCD中，AB＝AD＝CD＝1，BD＝，BD⊥CD.将四边形ABCD沿对角线BD折成四面体A′BCD，使平面A′BD⊥平面BCD，则下列结论正确的是(　　)‎ A．A′C⊥BD B．∠BA′C＝90°‎ C．CA′与平面A′BD所成的角为30°‎ D．四面体A′BCD的体积为 解析：选B.若A成立可得BD⊥A′D，产生矛盾，故A不正确；‎ 由题设知：△BA′D为等腰Rt△，CD⊥平面A′BD，得BA′⊥平面A′CD，于是B正确；‎ 由CA′与平面A′BD所成的角为∠CA′D＝45°知C不正确；‎ VA′BCD＝VCA′BD＝，D不正确．故选B.‎ ‎4．在直角梯形ABCD中，AB＝2，CD＝CB＝1，∠ABC＝90°，平面ABCD外有一点E，平面ADE⊥平面ABCD，AE＝ED＝1.‎ ‎(1)求证：AE⊥BE；‎ ‎(2)求点C到平面ABE的距离．‎ 解：(1)证明：在直角梯形ABCD中，BD＝＝，AD＝，又AD＝＝，所以AE⊥ED.‎ 因为AB2＝AD2＋BD2，‎ 所以AD⊥BD，‎ 因为平面ADE⊥平面ABCD，且交线为AD，AD⊥BD.‎ 所以BD⊥平面ADE.‎ 因为AE⊂平面ADE，所以BD⊥AE.‎ 因为AE⊥BD，AE⊥ED，BD∩DE＝D，‎ 所以AE⊥平面BDE，‎ 因为BE⊂平面BDE，所以AE⊥BE.‎ ‎(2)如图，过点E作EM⊥AD，交AD于M.‎ 因为平面ADE⊥平面ABCD，‎ 所以EM⊥平面ABCD.设点C到平面ABE的距离为h，‎ EM＝，S△ABC＝×AB×BC＝×2×1＝1，‎ S△ABE＝×EB×AE＝××1＝.‎ 因为VEABC＝VCABE，‎ 所以×1×＝××h，所以h＝，‎ 所以点C到平面ABE的距离为.‎ ‎5．(2018·太原模拟)如图，在几何体ABCDFE中，四边形ABCD是菱形，BE⊥平面ABCD，DF∥BE，且DF＝2BE＝2，EF＝3.‎ ‎(1)证明：平面ACF⊥平面BEFD.‎ ‎(2)若cos∠BAD＝，求几何体ABCDFE的体积．‎ 解：(1)证明：因为四边形ABCD是菱形，所以AC⊥BD，‎ 因为BE⊥平面ABCD，所以BE⊥AC.‎ 所以AC⊥平面BEFD.‎ 所以平面ACF⊥平面BEFD.‎ ‎(2)设AC与BD的交点为O，AB＝a(a>0)，‎ 由(1)得AC⊥平面BEFD，‎ 因为BE⊥平面ABCD，所以BE⊥BD，‎ 因为DF∥BE，所以DF⊥BD，‎ 所以BD2＝EF2－(DF－BE)2＝8，所以BD＝2，‎ 所以S四边形BEFD＝(BE＋DF)·BD＝3，‎ 因为cos∠BAD＝，所以BD2＝AB2＋AD2－2AB·AD·cos∠BAD＝a2＝8，‎ 所以a＝，‎ 所以OA2＝AB2－OB2＝3，所以OA＝，‎ 所以VABCDFE＝2VABEFD＝S四边形BEFD·OA＝2.‎ ‎6．(2017·高考全国卷Ⅲ)如图，四面体ABCD中，△ABC是正三角形，AD＝CD.‎ ‎(1)证明：AC⊥BD；‎ ‎(2)已知△ACD是直角三角形，AB＝BD.若E为棱BD上与D不重合的点，且AE⊥EC，求四面体ABCE与四面体ACDE的体积比．‎ 解：‎ ‎(1)证明：取AC的中点O，连接DO，BO.‎ 因为AD＝CD，所以AC⊥DO.‎ 又由于△ABC是正三角形，所以AC⊥BO.‎ 从而AC⊥平面DOB，故AC⊥BD.‎ ‎(2)连接EO.‎ 由(1)及题设知∠ADC＝90°，所以DO＝AO.‎ 在Rt△AOB中，BO2＋AO2＝AB2.‎ 又AB＝BD，所以 BO2＋DO2＝BO2＋AO2＝AB2＝BD2，故∠DOB＝90°.‎ 由题设知△AEC为直角三角形，所以EO＝AC.‎ 又△ABC是正三角形，且AB＝BD，所以EO＝BD.‎ 故E为BD的中点，从而E到平面ABC的距离为D到平面ABC的距离的，四面体ABCE的体积为四面体ABCD的体积的，即四面体ABCE与四面体ACDE的体积之比为1∶1.‎ ‎1．(2018·郑州第二次质量检测)如图，高为1的等腰梯形ABCD中，AM＝CD＝AB＝1，M为AB的三等分点．现将△AMD沿MD折起，使平面AMD⊥平面MBCD，连接AB，AC.‎ ‎(1)在AB边上是否存在点P，使AD∥平面MPC?‎ ‎(2)当点P为AB边的中点时，求点B到平面MPC的距离．‎ 解：(1)当AP＝AB时，有AD∥平面MPC.‎ 理由如下：‎ 连接BD交MC于点N，连接NP.‎ 在梯形MBCD中，DC∥MB，＝＝，‎ 因为△ADB中，＝，所以AD∥PN.‎ 因为AD⊄平面MPC，PN⊂平面MPC，‎ 所以AD∥平面MPC.‎ ‎(2)因为平面AMD⊥平面MBCD，平面AMD∩平面MBCD＝DM，‎ 平面AMD中AM⊥DM，所以AM⊥平面MBCD.‎ 所以VPMBC＝×S△MBC×＝××2×1×＝.‎ 在△MPC中，MP＝AB＝，MC＝，‎ 又PC＝＝，所以S△MPC＝××＝.‎ 所以点B到平面MPC的距离为d＝＝＝.‎ ‎2.‎ 如图所示，已知长方体ABCDA1B1C1D1，点O1为B1D1的中点．‎ ‎(1)求证：AB1∥平面A1O1D.‎ ‎(2)若AB＝AA1，在线段BB1上是否存在点E使得A1C⊥AE？若存在，求出；若不存在，说明理由．‎ 解：(1)证明：如图所示，连接AD1交A1D于点G，‎ 所以G为AD1的中点．连接O1G.在△AB1D1中，‎ 因为O1为B1D1的中点，‎ 所以O1G∥AB1.‎ 因为O1G⊂平面A1O1D，且AB1⊄平面A1O1D，‎ 所以AB1∥平面A1O1D.‎ ‎(2)若在线段BB1上存在点E使得A1C⊥AE，连接A1B交AE于点M.‎ 因为BC⊥平面ABB1A1，AE⊂平面ABB1A1，所以BC⊥AE.‎ 又因为A1C∩BC＝C，且A1C，BC⊂平面A1BC，‎ 所以AE⊥平面A1BC.‎ 因为A1B⊂平面A1BC，‎ 所以AE⊥A1B.‎ 在△AMB和△ABE中，‎ ‎∠BAM＋∠ABM＝90°，∠BAM＋∠BEA＝90°，‎ 所以∠ABM＝∠BEA.‎ 所以Rt△ABE∽Rt△A1AB，‎ 所以＝.‎ 因为AB＝AA1，‎ 所以BE＝AB＝BB1，‎ 即在线段BB1上存在点E使得A1C⊥AE，此时＝.‎ ‎3．(2018·福建质量检测)在如图所示的多面体中，四边形ABCD是平行四边形，四边形BDEF是矩形．‎ ‎(1)求证：AE∥平面BCF；‎ ‎(2)若AD⊥DE，AD＝DE＝1，AB＝2，∠BAD＝60°，求三棱锥FAEC的体积．‎ 解：(1)证明：因为四边形ABCD是平行四边形，‎ 所以AD∥BC.‎ 又AD⊄平面BCF，BC⊂平面BCF，所以AD∥平面BCF，因为四边形BDEF是矩形，所以DE∥BF.又DE⊄平面BCF，BF⊂平面BCF，‎ 所以DE∥平面BCF.‎ 因为AD∩DE＝D，AD⊂平面ADE，DE⊂平面ADE，‎ 所以平面ADE∥平面BCF.‎ 因为AE⊂平面ADE，所以AE∥平面BCF.‎ ‎(2)设AC与BD交于点O，则O为AC的中点．连接OE，OF，如图．‎ 故VFAEC＝VCAEF＝2VOAEF＝2VAOEF.‎ 在△ABD中，∠BAD＝60°，AD＝1，AB＝2，‎ 由余弦定理得，BD2＝AB2＋AD2－2AB·AD·cos∠BAD，‎ 所以BD＝，‎ 所以AB2＝AD2＋BD2，所以AD⊥BD.‎ 又DE⊥AD，BD∩DE＝D，BD⊂平面BDEF，DE⊂平面BDEF，所以AD⊥平面BDEF，‎ 故AD的长为点A到平面BDEF的距离．‎ 因为DE＝1，所以S△OEF＝S四边形BDEF＝BD·DE＝，所以VAOEF＝S△OEF·AD＝，‎ 故VFAEC＝2VAOEF＝，即三棱锥FAEC的体积为.‎