【数学】2019届一轮复习北师大版正弦定理和余弦定理学案 12页

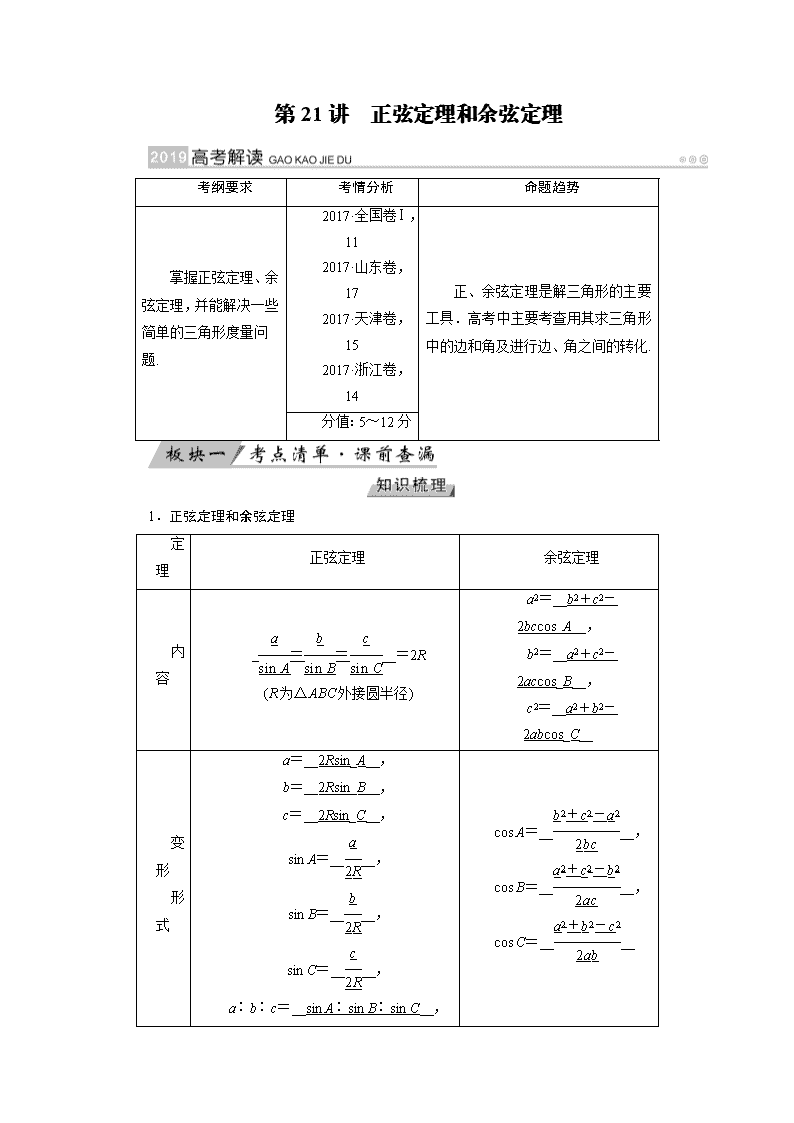
第21讲　正弦定理和余弦定理 考纲要求 考情分析 命题趋势 掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题.‎ ‎2017·全国卷Ⅰ，11‎ ‎2017·山东卷，17‎ ‎2017·天津卷，15‎ ‎2017·浙江卷，14‎ 正、余弦定理是解三角形的主要工具．高考中主要考查用其求三角形中的边和角及进行边、角之间的转化.‎ 分值：5～12分 ‎1．正弦定理和余弦定理 定理 正弦定理 余弦定理 内容 ‎ ＝＝__＝2R ‎(R为△ABC外接圆半径)‎ a2＝__b2＋c2－2bccos_A__，‎ b2＝__a2＋c2－2accos_B__，‎ c2＝__a2＋b2－2abcos_C__‎ 变形 形式 a＝__2Rsin_A__，‎ b＝__2Rsin_B__，‎ c＝__2Rsin_C__，‎ sin A＝____，‎ sin B＝____，‎ sin C＝____，‎ a∶b∶c＝__sin A∶sin B∶sin C__，‎ 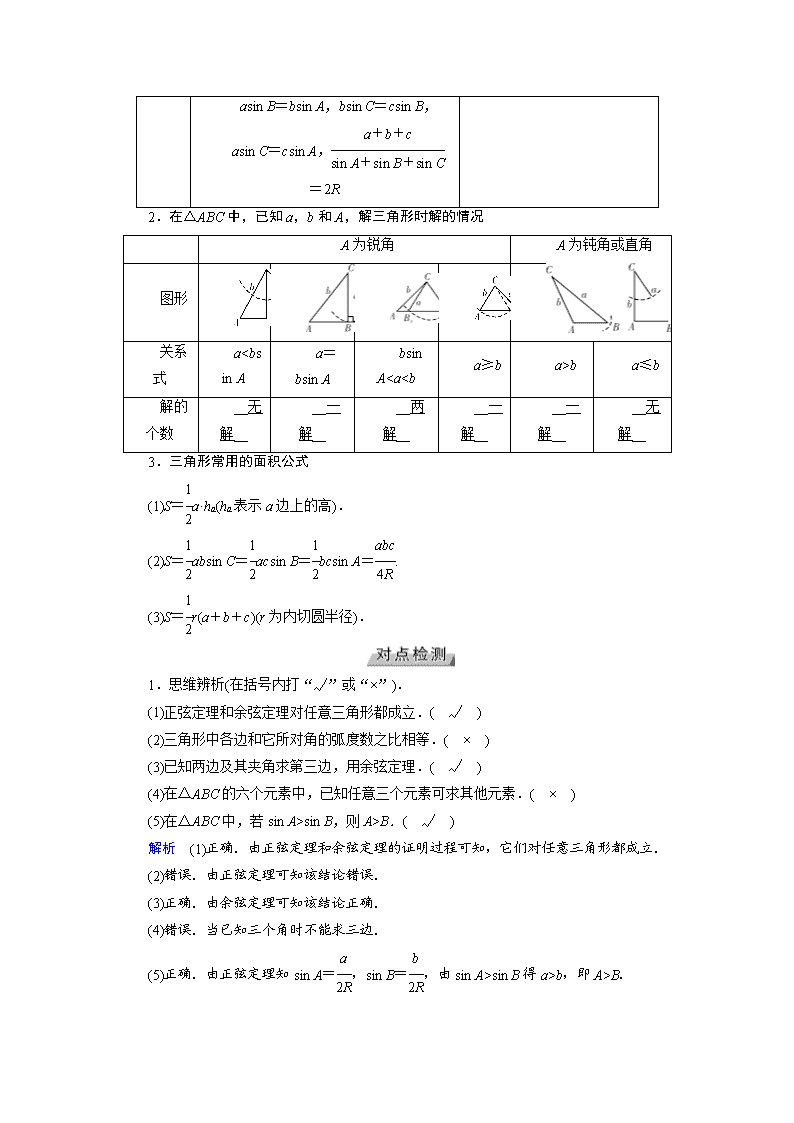asin B＝bsin A，bsin C＝csin B，‎ cos A＝____，‎ cos B＝____，‎ cos C＝____‎ asin C＝csin A，＝2R ‎2．在△ABC中，已知a，b和A，解三角形时解的情况 A为锐角 A为钝角或直角 图形 关系式 ab a≤b 解的个数 ‎__无解__‎ ‎__一解__‎ ‎__两解__‎ ‎__一解__‎ ‎__一解__‎ ‎__无解__‎ ‎3．三角形常用的面积公式 ‎(1)S＝a·ha(ha表示a边上的高)．‎ ‎(2)S＝absin C＝acsin B＝bcsin A＝.‎ ‎(3)S＝r(a＋b＋c)(r为内切圆半径)．‎ ‎1．思维辨析(在括号内打“√”或“×”)．‎ ‎(1)正弦定理和余弦定理对任意三角形都成立．(　√　)‎ ‎(2)三角形中各边和它所对角的弧度数之比相等．(　×　)‎ ‎(3)已知两边及其夹角求第三边，用余弦定理．(　√　)‎ ‎(4)在△ABC的六个元素中，已知任意三个元素可求其他元素．(　×　)‎ ‎(5)在△ABC中，若sin A>sin B，则A>B．(　√　)‎ 解析　(1)正确．由正弦定理和余弦定理的证明过程可知，它们对任意三角形都成立．‎ ‎(2)错误．由正弦定理可知该结论错误．‎ ‎(3)正确．由余弦定理可知该结论正确．‎ ‎(4)错误．当已知三个角时不能求三边．‎ ‎(5)正确．由正弦定理知sin A＝，sin B＝，由sin A>sin B得a>b，即A>B．‎ ‎2．在△ABC中，若∠A＝60°，∠B＝45°，BC＝3，则AC＝(　B　)‎ A．4　　 B．‎2‎　　‎ C．　　 D． 解析　由正弦定理得＝，即＝，‎ 所以AC＝×＝2.‎ ‎3．在△ABC中，a＝，b＝1，c＝2，则∠A＝(　C　)‎ A．30°　　 B．45°　　‎ C．60°　　 D．75°‎ 解析　∵cos A＝＝＝，且0°0，∴B为锐角，sin B＝.‎ ‎∵sin A2，∴三角形仅有一解，∴c＝3.设BC边上的高为h，则h＝csin B＝.‎ ‎5．钝角三角形ABC的面积是，AB＝1，BC＝，则AC＝(　B　)‎ A．5　　 B．　　‎ C．2　　 D．1‎ 解析　S＝AB·BCsin B＝×1×sin B＝，∴sin B＝，∴B＝或.当B＝时，根据余弦定理得AC ‎2＝AB2＋BC2－2AB·BCcos B＝1＋2＋2＝5，∴AC＝，此时△ABC为钝角三角形，符合题意；当B＝时，根据余弦定理得AC2＝AB2＋BC2－2AB·BCcos B＝1＋2－2＝1，∴AC＝1，此时AB2＋AC2＝BC2，△ABC为直角三角形，不符合题意，故AC＝.‎ ‎6．在△ABC中，内角A，B，C所对的边分别是a，b，c.若c2＝(a－b)2＋6，C＝，则△ABC的面积是(　C　)‎ A．3　　 B．　　‎ C．　　 D．3 解析　∵c2＝(a－b)2＋6，∴c2＝a2＋b2－2ab＋6.①‎ ‎∵C＝，∴c2＝a2＋b2－2abcos＝a2＋b2－ab.②‎ 由①②，得－ab＋6＝0，即ab＝6.‎ ‎∴S△ABC＝absin C＝×6×＝.‎ 二、填空题 ‎7．△ABC的内角A，B，C所对的边分别为a，b，c，且a，b，c成等比数列．若sin B＝，cos B＝，则a＋c的值为__3__.‎ 解析　∵a，b，c成等比数列，∴b2＝ac.∵sin B＝，cos B＝，∴ac＝13，∴b2＝a2＋c2－2accos B，∴a2＋c2＝37，∴(a＋c)2＝63，∴a＋c＝3.‎ ‎8．(2017·浙江卷)已知△ABC，AB＝AC＝4，BC＝2.点D为AB延长线上一点，BD＝2，连接CD，则△BDC的面积是____，cos∠BDC＝____.‎ 解析　在△ABC中，AB＝AC＝4，BC＝2，由余弦定理得cos∠ABC＝＝＝，则sin∠ABC＝sin∠CBD＝，所以S△BDC＝BD·BCsin∠CBD＝.因为BD＝BC＝2，所以∠BDC＝∠ABC，则cos∠BDC＝＝.‎ ‎9．在△ABC中，内角A，B，C所对的边分别是a，b，c.若b－c＝a，2sin B＝3sin C，则cos A的值为__－__.‎ 解析　由2sin B＝3sin C及正弦定理得2b＝‎3c，即b＝c.又∵b－c＝a，∴c＝a，即a＝‎ ‎2c‎.由余弦定理，得cos A＝＝＝＝－.‎ 三、解答题 ‎10．(2018·河北邢台质检)在△ABC中，内角A，B，C的对边分别是a，b，c，且b＝2asin B，tan A＞0.‎ ‎(1)求角A的大小；‎ ‎(2)若b＝1，c＝2，△ABC的面积为S，求.‎ 解析　(1)∵b＝2asin B，∴sin B＝2sin A·sin B，sin B>0，‎ ‎∴sin A＝，∵tan A>0，∴A为锐角，∴A＝.‎ ‎(2)∵a2＝b2＋c2－2bccos A＝1＋12－4×＝7，∴a＝.‎ 又S＝bcsin A＝，∴＝.‎ ‎11．(2018·河南重点高中期中)在△ABC中，内角A，B，C的对边分别为a，b，c，且sin2＝.‎ ‎(1)判断△ABC的形状并加以证明；‎ ‎(2)当c＝1时，求△ABC周长的最大值．‎ 解析　(1)∵＝－，即cos A＝，‎ ‎∴b＝ccos A＝c·，即c2＝b2＋a2，‎ ‎∴△ABC为直角三角形．‎ ‎(2)∵c为直角△ABC的斜边，当c＝1时，‎ 周长L＝1＋sin A＋cos A＝1＋sin.‎ ‎∵0c.已知·＝2，cos B＝，b＝3，求：‎ ‎(1)a和c的值；‎ ‎(2)cos(B－C)的值．‎ 解析　(1)由·＝2，得c·acos B＝2，又cos B＝，所以ac＝6.‎ 由余弦定理，得a2＋c2＝b2＋2accos B．又b＝3，所以a2＋c2＝9＋2×2＝13.由解得a＝2，c＝3或a＝3，c＝2.‎ 因为a>c，所以a＝3，c＝2.‎ ‎(2)在△ABC中，sin B＝＝＝.‎ 由正弦定理，得sin C＝sin B＝×＝.‎ 因为a＝b>c，所以C为锐角，因此cos C＝＝＝.于是cos(B－C)＝cos Bcos C＋sin B·sin C＝×＋×＝.‎