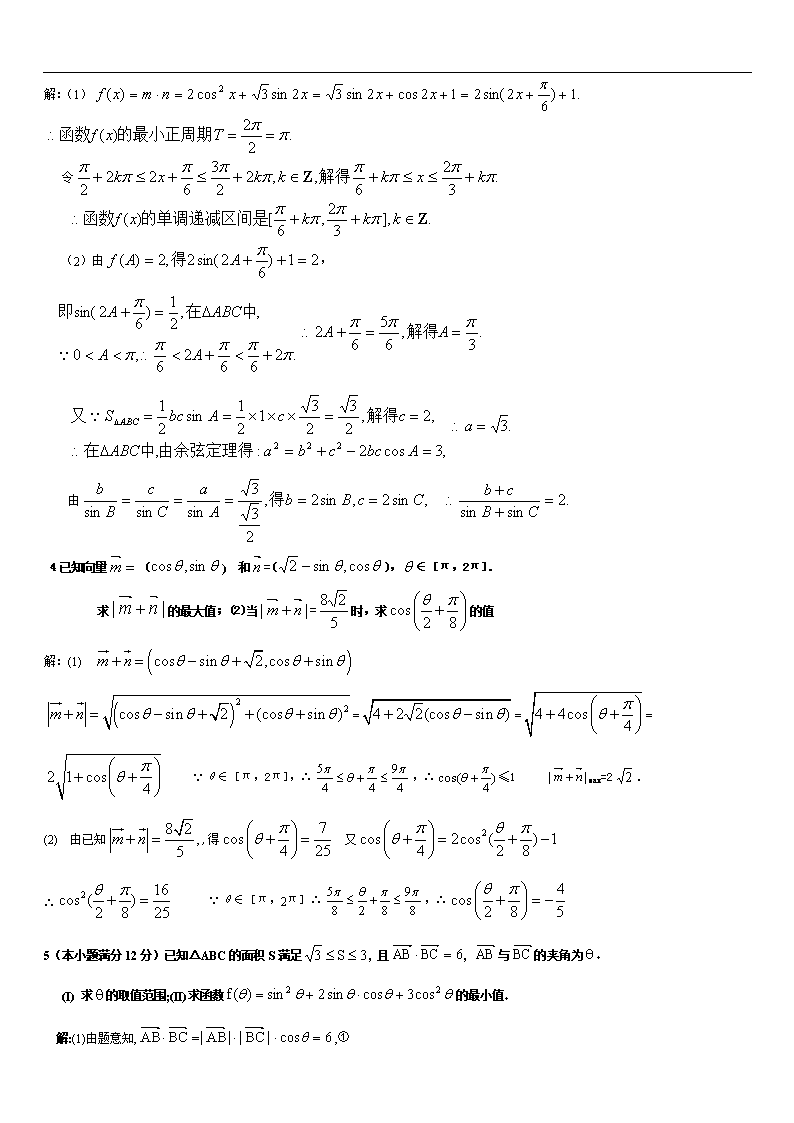高考数学专题复习（精选精讲）练习4-三角函数与向量习题精选精讲 4页

三角函数与向量 ‎1已知向量=（sinB，1－cosB），且与向量=（2，0）的夹角为，其中A, B, C是ABC的内角．（I）求角Ｂ的大小； （II）求sinA+sinC的取值范围 解：（1）∵=（sinB，1-cosB） , 且与向量（2，0）所成角为 ‎∴∴tan 第一问：另解：∵ , 且与向量所成角为 ‎∴ ，∴，又，∴ ，即 ‎ ‎（2）：由（1）可得∴∵∴∴‎ 当且仅当 ‎2．已知、、三点的坐标分别为、、，，‎ ‎（I）若，求角的值；（II）若，求的值 解：（1）‎ ‎， 由得 又 ‎ ‎（2）由，得 ‎ 又=‎ 所以，=。‎ ‎3．设函数 ‎ （1）求的最小正周期与单调递减区间；（2）在△ABC中，a、b、c分别是角A、B、C的对边，已知，△ABC的面积为的值。‎ 解：（1）‎ ‎ 令 ‎ ‎ ‎ （2）由，‎ ‎ ‎ ‎ ‎ ‎ 由 ‎ ‎4已知向量 () 和=()，∈［π，2π］．‎ 求的最大值；(2)当=时，求的值 解：(1) ‎ ‎=== ∵θ∈［π，2π］，∴，∴≤1 max=2． ‎ (2) 由已知,得 又 ‎ ‎∴ ∵θ∈［π，2π］∴，∴‎ ‎5（本小题满分12分）已知△ABC的面积S满足, 且, 与的夹角为 ‎ ‎(I) 求的取值范围;(II)求函数的最小值 ‎ ‎ 解:(1)由题意知,,①‎ ‎,②‎ 由②÷①, 得, 即由得, 即 ‎ 又为与的夹角, ∴, ∴ ‎ ‎(2)‎ ‎∵, ∴‎ ‎∴, 即时, 的最小值为3 ‎ ‎6已知的面积为，且满足，设和的夹角为．‎ ‎（I）求的取值范围；（II）求函数的最大值与最小值．‎ ‎【解析】（Ⅰ）设中角的对边分别为，‎ 则由，，可得，．‎ ‎（Ⅱ）‎ ‎．‎ ‎，，．即当时，；当时，．‎ ‎7．已知、‎ ‎ （1）求向量的夹角； （2）求、的值.‎ 解：（1） ‎ ‎ ‎ ‎ ‎ ‎ 又 ‎ （2）由（1）可知，‎ ‎ 将代入.‎ ‎8． 已知锐角△ABC中，三个内角为A、B、C，两向量，‎ 是共线向量.‎ ‎ （1）求A的大小；‎ ‎ （2）求函数取最大值时，B的大小 ‎．解析：（1）‎ ‎ （3分）‎ ‎ 化简得： （4分）‎ ‎ 因为△ABC为锐角三形， （6分）‎ ‎ （2）‎ ‎ ‎ ‎ （10分）‎ ‎ ‎