【数学】2019届一轮复习北师大版不等式应用学案 9页

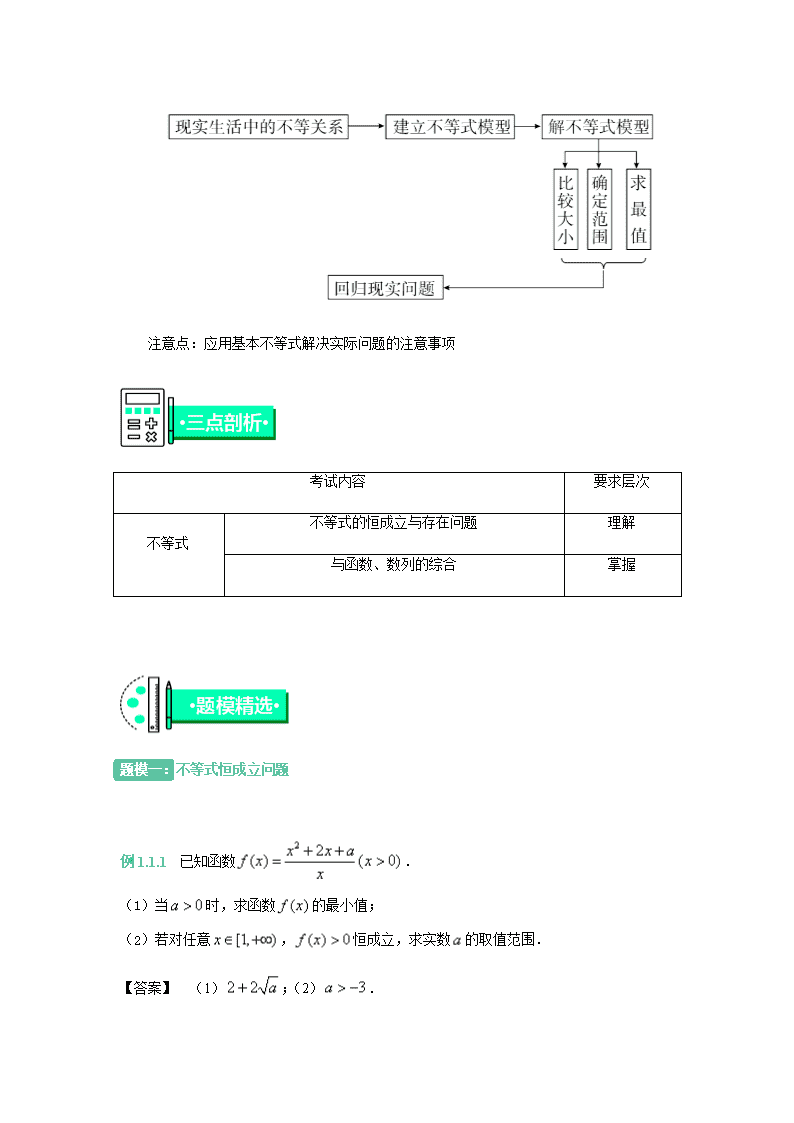
‎ 不等式应用 知识精讲·‎ ‎·‎ 一．不等式的恒成立、存在性、恰成立等问题 ‎1．恒成立问题：若在区间上存在最小值，则不等式在区间上恒成立()；‎ 若在区间上存在最大值，则不等式在区间上恒成立 ()．‎ ‎2．存在性问题：若在区间上存在最大值，则在区间上存在实数使不等式成立()；‎ 若在区间上存在最小值，则在区间上存在实数使不等式成立 ()．‎ ‎3．恰成立问题：不等式在区间上恰成立的解集为；‎ 不等式在区间上恰成立的解集为．‎ 二．解不等式的实际应用题的一般步骤 注意点：应用基本不等式解决实际问题的注意事项 ‎·三点剖析·‎ ‎·‎ 考试内容 要求层次 不等式 不等式的恒成立与存在问题 理解 与函数、数列的综合 掌握 ‎·题模精选·‎ ‎·‎ 题模一：不等式恒成立问题 例1.1.1 已知函数．‎ ‎（1）当时，求函数的最小值；‎ ‎（2）若对任意，恒成立，求实数的取值范围．‎ ‎【答案】 （1）；（2）．‎ ‎【解析】 （1），当且仅当即时，等号成立，所以函数的最小值为；‎ ‎（2）在区间上，恒成立，等价于恒成立，即在上恒成立．因为函数在上的最大值为，所以．‎ 例1.1.2 已知函数．‎ ‎（1）若的解集为，则的值等于　 　；‎ ‎（2）对任意，恒成立，则的取值范围是　 　．　‎ ‎【答案】 （1）；（2）．‎ ‎【解析】 （1）．‎ 由已知是其解集，‎ 得的两根是，．‎ 由根与系数的关系可知，‎ 解得，‎ ‎（2）对任意，恒成立，等价于恒成立，‎ ‎∵，当且仅当时取等号，‎ ‎∴，‎ 故答案为：（1）；（2） ‎ 题模二：不等式的存在问题 例1.2.1 若不存在整数x使不等式（ x- 2-4）（x-4）＜0成立，则实数 的取值范围是____．‎ ‎【答案】 1≤ ≤4‎ ‎【解析】 ‎ 设原不等式的解集为A，‎ 当 =0时，则x＞4，不合题意，‎ 当 ＞0且 ≠2时，原不等式化为[x-（ +） （x-4）＜0，‎ ‎∵ +＞4，‎ ‎∴A=(4， +)，要使不存在整数x使不等式（ x- 2-4）（x-4）＜0成立，‎ 须 +≤5，解得：1≤ ≤4；‎ 当 =2时，A=∅，合题意，‎ 当 ＜0时，原不等式化为[x-（ +） （x-4）＞0，‎ ‎∴A=（-∞， +）∪（4，+∞），不合题意，‎ 故答案为：1≤ ≤4．‎ 例1.2.2 已知函数，若存在使得成立，则实数a 的取值范围为．‎ ‎【答案】 （-∞，-15 ‎ ‎【解析】 f（x）≤2，即为 ≤2，‎ 由xÎN ，可得3x2+（a-2）x+24≤0，‎ 即有2-a≥=3x+，‎ 由3x+≥2 =12，‎ 当且仅当x=2∉N，‎ 由x=2可得6+12=18；x=3时，可得9+8=17，‎ 可得3x+的最小值为17，‎ 由存在xÎN 使得f（x）≤2成立，‎ 可得2-a≥17，‎ 解得a≤-15．‎ 题模三：函数与不等式的综合 例1.3.1 某公司一年购买某种货物600吨，每次都购买吨，运费为3万元/次，一年的总存储费用为万元，若要使一年的总运费与总存储费用之和最小，则每次需购买 吨．‎ ‎【答案】 30‎ ‎【解析】 设公司一年的总运费与总存储费用之和为万元．买货物600吨，每次都购买吨，‎ 则需要购买的次数为次，因为每次的运费为3万元，则总运费为万元．所以 ‎．则．当且仅当，即 时取得最小值．所以，要使一年的总运费与总存储费用之和最小，则每次需购买30‎ 吨．故答案为30．‎ 例1.3.2 某车间分批生产某种产品，每批的生产准备费用为800元．若每批生产件，则平 均仓储时间为天，且每件产品每天的仓储费用为1元．为使平均到每件产品的生产准备 费用与仓储费用之和最小，每批应生产产品 A． 60件 B． 80件 C． 100件 D． 120件 ‎【答案】B ‎【解析】 仓储费用，每件产品的生产准备费用与仓储费用之和当且仅当即上式取等号，所以每批应生产产品件，故选B．‎ ‎·随堂练习·‎ ‎·‎ 随练1.1 当x＞1时，不等式x+≥a恒成立，则实数a的取值范围是 ____．‎ ‎【答案】‎ ‎【解析】 本题主要考查了基本不等式在最值问题中的应用．注意等号成立的条件，当等号不成立时刻利用函数的单调性来解决．‎ 先判断出f（x）=x+在（1，+∞）上单调性，进而利用x的范围确定f（x）的范围，进而利用题设不等式恒成立求得a的范围．‎ ‎∵f（x）=x+在（1，+∞）上单调增 ‎∴f（x）＞1+=‎ ‎∵x+≥a恒成立 ‎∴a≤‎ 故答案为：a≤‎ 随练1.2 存在实数，使得成立，则的取值范围是____．‎ ‎【答案】 ‎ ‎【解析】 因为存在实数x，使得x2-4bx+3b＜0成立的等价说法是：‎ 存在实数x，使得函数y=x2-4bx+3b的图象在轴下方，‎ 即函数与轴有两个交点，故对应的△=（-4b）2-4×3b＞0⇒b＜0或b＞．‎ 故答案为：b＜0或b＞．‎ 随练1.3 在如图所示的等边三角形空地中，欲建一个内接矩形花园（阴影部分），则此矩形面积的最大值为（ ）‎ A． ‎ B． ‎ C． ‎ D． ‎ ‎【答案】D ‎【解析】 设矩形的长为，则宽为，‎ 所以矩形面积，‎ 当且仅当时等号成立，‎ 故矩形面积最大值为．‎ ‎·自我总结·‎ ‎·‎ ‎ ‎ ‎·课后作业·‎ ‎·‎ 作业1 已知f（x）=m（x-2m）（x+m+3），g（x）=2x-2．若∀x∈R，f（x）＜0或g（x）＜0，则m的取值范围是____．‎ ‎【答案】 （-4，0）‎ ‎【解析】 ‎ ‎∵g（x）=2x-2，当x≥1时，g（x）≥0，‎ 又∵∀x∈R，f（x）＜0或g（x）＜0‎ ‎∴此时f（x）=m（x-2m）（x+m+3）＜0在x≥1时恒成立 若m=0，f(x)=0恒成立，不符合，故m≠0‎ 则由二次函数的性质可知开口只能向下，且二次函数与x轴交点都在（1，0）的左面 则 ‎∴-4＜m＜0‎ 故答案为：（-4，0）‎ 作业2 建造一个容积为8m3，深为2m的长方体无盖水池，如果池底和池壁的造价每平方米分别为120元和80元，则水池的最低造价为 ____．‎ ‎【答案】 1760元 ‎【解析】 ‎ 设长x，则宽，造价y=4×120+4x•80+×80≥1760，‎ 当且仅当：4x•80=×80，即x=2时取等号．‎ 故答案为：1760元．‎