【数学】2019届一轮复习北师大版玩转一题，学透平面向量学案 10页

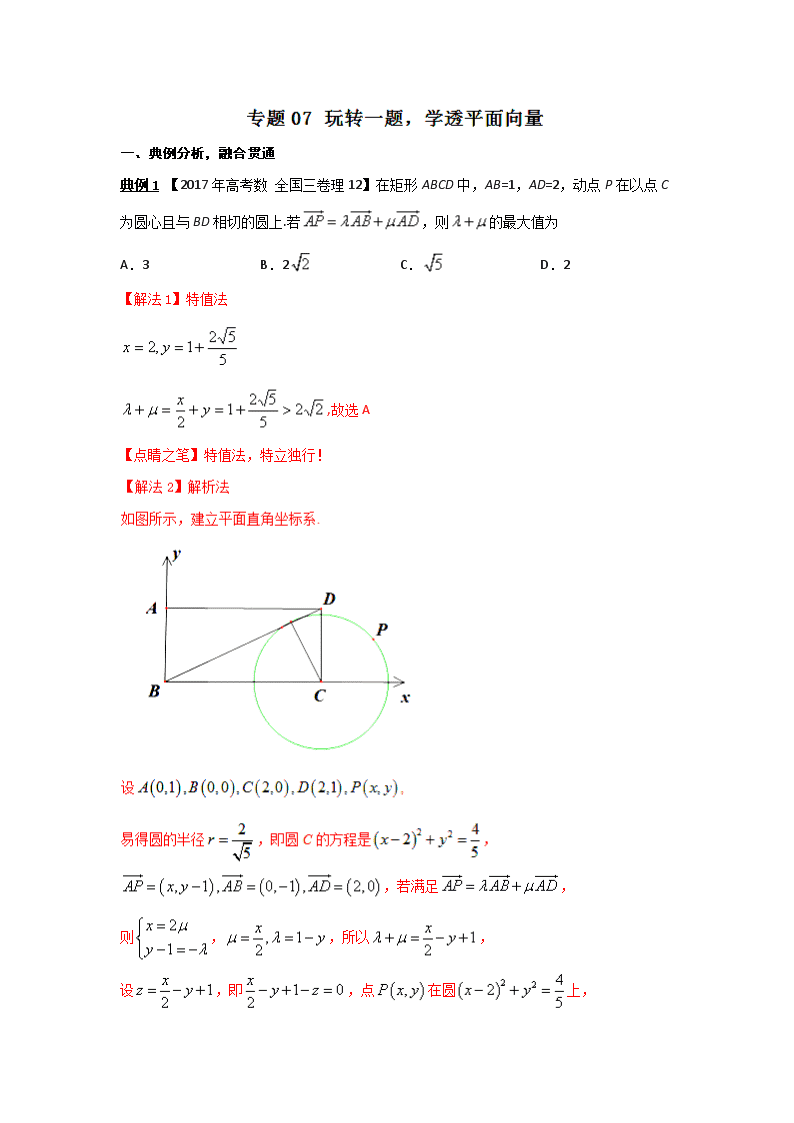
一、典例分析，融合贯通 ‎ 典例1 【2017年高考数 全国三卷理12】在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上.若，则的最大值为 A．3 B．2 C． D．2‎ ‎【解法1】特值法 ‎,故选A ‎【点睛之笔】特值法，特立独行！‎ ‎ ，若满足，‎ 则，，所以，‎ 设，即，点在圆上， ]‎ 所以圆心到直线的距离，即，解得，‎ 所以的最大值是 ，即的最大值是，故选A.‎ ‎【点睛之笔】解析法，用数据说话！‎ ‎【点睛之笔】等和线法，等你 和一把！ ‎ ‎【解后反思】[ ]‎ 解法1 特值法，四两拨千斤，化难为易！‎ 解法2 解析法，用数据说话，降低思维量！‎ 解法3 等和线法，在移动中联通彼岸！‎ 典例2 【2017年高考数 天津卷理12】（13）在中，，，.若，，且，则的值为 ‎___________.‎ ‎【解法1】几何法 ‎【点睛之笔】几何法，以形助数，不攻自破！‎ ‎【点睛之笔】解析法,“数点”江山！‎ ‎【解法3】等量代换法 ‎，因此，‎ 结合，因此，即 ‎，即，即.‎ ‎【点睛之笔】等量代换法，一代胜一代！ ‎ ‎【解后反思】‎ 解法1 几何法，利用向量三角形法则，“减”掉 难点！‎ 解法2 解析法，用数据稀释难点，让问题 得再难一点吧！‎ 解法3 等量代换法，当换则换，不换则乱！‎ 典例3【2017年高考数 全国二卷理12】已知是边长为2的等边三角形，P为平面ABC内一点，则的最小值是（ ）‎ A. B. C. D. ‎ ‎【解法1】坐标法 以 为 轴，的垂直平分线为 轴为坐标原点建立=坐标系，则 ‎ ‎【点睛之笔】坐标法，用坐标“量取”答案！‎ ‎【解法2】极化恒等式 取的中点为，则，于是，根据极化恒等式可得 ‎，故选B.‎ ‎【点睛之笔】极化恒等式，“激发”我们的数 灵感！‎ ‎【点睛之笔】代数法，用数“指点”江山！ ‎ ‎【解后反思】‎ 解法1 坐标法，以数辅形，如探囊取物也！‎ 解法2 极化恒等式，剑走偏锋，颇显灵气！‎ 解法3 代数法，借助函数思想，化难为易！‎ 二、精选试题，能力升级 ‎1．【2018河北石家庄二中八月模拟】在中， ，点是所在平面内一点，则当取得最小值时， ( )‎ A. 9 B. C. D. ‎ ‎【答案】B ‎ 2．【2018浙江温州一模】已知的边的垂直平分线交于，交于，若，，则的值为（ ）‎ A. 3 B. C. D. ‎ ‎【答案】B ‎【解析】因为的垂直平分线交于，所以 ， ，故选B.‎ ‎3．【2018吉林省百校联盟九月联考】已知单位向量与的夹角为，向量与的夹角为，则（ ）‎ A. B. C. 或 D. 或 ‎【答案】B ‎ 本题选择B选项. ‎ ‎4．【2018辽宁省大连八中模拟】设向量满足，则 ( )‎ A. 6 B. C. 10 D. ‎ ‎【答案】D ‎【解析】,，‎ ‎，‎ ‎，选D.‎ ‎5．【2018广东广州珠海区一模】已知向量的夹角为，则（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】由，得，即，则，解得（舍去）或，故选D.‎ ‎6．【2018海南省八校联考】设为线段的中点，且，则( )‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】由为线段的中点，且，得 2， ，即 故选 D ‎7．【2018湖南省永州市一模】已知， ， ，若与平行，则（ ）‎ A. -1 B. 1 C. 2 D. 3‎ ‎【答案】A ‎ ‎ ‎8. 【2014全国1，文6】设分别为的三边的中点，则 A. B. C. D. ‎ ‎【答案】A ‎【解析】根据平面向量基本定理和向量的加减运算可得 在中，，同理，则[ ]‎ ‎9. 【2012全国1，文9】△ABC中，AB边的高为CD．若＝a，＝b，a·b＝0，|a|＝1，|b|＝2，则＝(　　)‎ A． B． C． D．‎ ‎【答案】D　‎ ‎ ‎ ‎10. 【2010全国1，文11】已知圆O的半径为1，PA、PB为该圆的两条切线，A、B为两切点，那么·的最小值为(　　)[ ]‎ A．－4＋ B．－3＋ C．－4＋2 D．－3＋2‎ ‎【答案】 D　‎ ‎【解析】如图，设 ‎ ‎ ‎ ‎ ‎ 当且仅当，即时，等号成立,故选D.‎