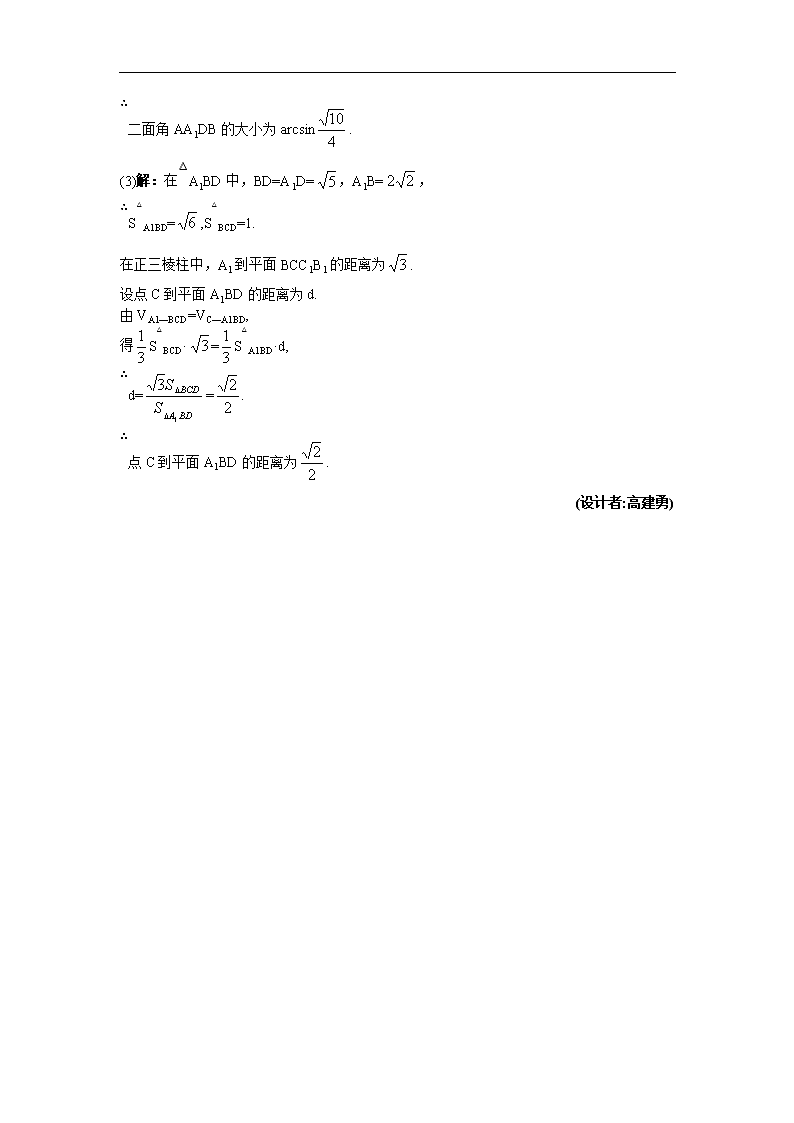高中数学必修2教案11_备课资料（2_3_4 平面与平面垂直的性质） 2页

备课资料 备用习题 ‎(2007福建高考,理18)如图22，正三棱柱ABC—A1B1C1的所有棱长都为2,D为CC1中点.‎ 图22‎ ‎（1）求证：AB1⊥平面A1BD；‎ ‎（2）求二面角AA1DB的大小；‎ ‎（3）求点C到平面A1BD的距离.‎ 分析：本小题主要考查直线与平面的位置关系，二面角的大小，点到平面的距离等知识，考查空间想象能力、逻辑思维能力和运算能力.‎ ‎（1）证明：如图23,取BC中点O，连接AO.‎ 图23‎ ‎∵△ABC为正三角形，‎ ‎∴AO⊥BC.‎ ‎∵在正三棱柱ABC—A1B1C1中，平面ABC⊥平面BCC1B1，‎ ‎∴AO⊥平面BCC1B1.‎ 连接B1O，在正方形BB1C1C中，O、D分别为BC、CC1的中点，‎ ‎∴B1O⊥BD.∴AB1⊥BD.‎ 在正方形ABB1A1中，AB1⊥A1B,‎ ‎∴AB1⊥平面A1BD.‎ ‎（2）解：设AB1与A1B交于点G，在平面A1BD中，作GF⊥A1D于F，连接AF，由（1）,得AB1⊥平面A1BD，‎ ‎∴AF⊥A1D.‎ ‎∴∠AFG为二面角AA1DB的平面角.‎ 在△AA1D中，由等面积法可求得AF=,‎ 又∵AG=AB1=，‎ ‎∴sin∠AFG=.‎ ‎∴二面角AA1DB的大小为arcsin.‎ ‎(3)解：在△A1BD中，BD=A1D=，A1B=，‎ ‎∴S△A1BD=,S△BCD=1.‎ 在正三棱柱中，A1到平面BCC1B1的距离为.‎ 设点C到平面A1BD的距离为d.‎ 由VA1—BCD=VC—A1BD,‎ 得S△BCD·=S△A1BD·d,‎ ‎∴d==.‎ ‎∴点C到平面A1BD的距离为.‎ ‎(设计者:高建勇)‎