【数学】2018届一轮复习苏教版（理）直线与圆的位置关系教案（江苏专用） 16页

第70课 直线与圆的位置关系 ‎[最新考纲]‎ 内容 要求 A B C 圆的切线的判定与性质定理 ‎√‎ 圆周角定理，弦切角定理 ‎√‎ 相交弦定理，割线定理，切割线定理 ‎√‎ 圆内接四边形的判定与性质定理 ‎√‎ ‎1．圆周角与圆心角定理 ‎(1)圆心角定理：圆心角的度数等于其所对弧的度数．‎ ‎(2)圆周角定理：圆周角的度数等于其所对弧的度数的一半．‎ 推论1：同弧(或等弧)所对的圆周角相等．同圆或等圆中，相等的圆周角所对的弧相等．‎ 推论2：半圆(或直径)所对的圆周角等于90°.反之，90°的圆周角所对的弧为半圆(或弦为直径)．‎ ‎2．圆的切线的性质及判定定理 ‎(1)判定定理：过半径外端且与这条半径垂直的直线是圆的切线．‎ ‎(2)性质定理：圆的切线垂直于经过切点的半径．‎ 推论1：经过圆心且与切线垂直的直线必经过切点．‎ 推论2：经过切点且与切线垂直的直线必经过圆心．‎ ‎3．切线长定理 从圆外一点引圆的两条切线，切线长相等．‎ ‎4．弦切角定理 弦切角的度数等于其所夹弧的度数的一半．‎ ‎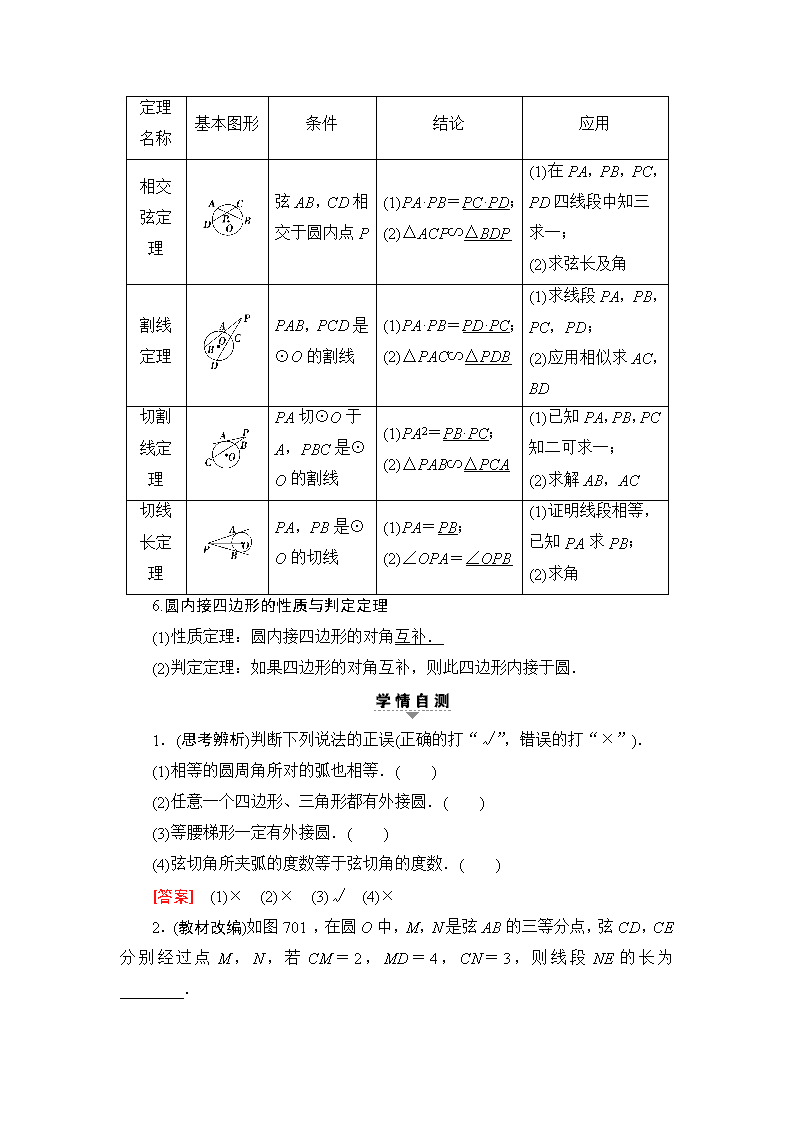5．与圆有关的比例线段 定理 名称 基本图形 条件 结论 应用 相交 弦定 理 弦AB，CD相交于圆内点P ‎(1)PA·PB＝PC·PD；‎ ‎(2)△ACP∽△BDP ‎(1)在PA，PB，PC，PD四线段中知三求一；‎ ‎(2)求弦长及角 割线 定理 PAB，PCD是⊙O的割线 ‎(1)PA·PB＝PD·PC；‎ ‎(2)△PAC∽△PDB ‎(1)求线段PA，PB，PC，PD；‎ ‎(2)应用相似求AC，BD 切割 线定 理 PA切⊙O于A，PBC是⊙O的割线 ‎(1)PA2＝PB·PC；‎ ‎(2)△PAB∽△PCA ‎(1)已知PA，PB，PC知二可求一；‎ ‎(2)求解AB，AC 切线 长定 理 PA，PB是⊙O的切线 ‎(1)PA＝PB；‎ ‎(2)∠OPA＝∠OPB ‎(1)证明线段相等，已知PA求PB；‎ ‎(2)求角 ‎6.圆内接四边形的性质与判定定理 ‎(1)性质定理：圆内接四边形的对角互补．‎ ‎(2)判定定理：如果四边形的对角互补，则此四边形内接于圆．‎ ‎1．(思考辨析)判断下列说法的正误(正确的打“√”，错误的打“×”)．‎ ‎(1)相等的圆周角所对的弧也相等．(　　)‎ ‎(2)任意一个四边形、三角形都有外接圆．(　　)‎ ‎(3)等腰梯形一定有外接圆．(　　)‎ ‎(4)弦切角所夹弧的度数等于弦切角的度数．(　　)‎ ‎[答案]　(1)×　(2)×　(3)√　(4)×‎ ‎2．(教材改编)如图701，在圆O中，M，N是弦AB的三等分点，弦CD，CE分别经过点M，N，若CM＝2，MD＝4，CN＝3，则线段NE的长为________．‎ 图701‎ 　[由题意可设AM＝MN＝NB＝x，由圆的相交弦定理得 即 解得x＝2，NE＝.]‎ ‎3．(教材改编)如图702，P为⊙O外一点，过P作⊙O的两条切线，切点分别为A，B，过PA的中点Q作割线交⊙O于C，D两点，若QC＝1，CD＝3，则PB＝________.‎ 图702‎ ‎4　[由切割线定理得QA2＝QC·QD＝1×(1＋3)＝4，‎ 所以QA＝2，PB＝PA＝4.]‎ ‎4．(2016·天津高考)如图703，AB是圆的直径，弦CD与AB相交于点E，BE＝2AE＝2，BD＝ED，则线段CE的长为________．‎ 图703‎ 　[如图，设圆心为O，连结OD，则OB＝OD.‎ 因为AB是圆的直径，BE＝2AE＝2，所以AE＝1，OB＝.‎ 又BD＝ED，∠B为△BOD与△BDE的公共底角，‎ 所以△BOD∽△BDE，所以＝，‎ 所以BD2＝BO·BE＝3，所以BD＝DE＝.‎ 因为AE·BE＝CE·DE，所以CE＝＝.]‎ ‎5．如图704，AB是圆O的直径，C，D是圆O上位于AB异侧的两点，证明：∠OCB＝∠D.‎ 图704‎ ‎[证明]　因为B，C是圆O上的两点，所以OB＝OC，‎ 故∠OCB＝∠B.‎ 又因为C，D是圆O上位于AB异侧的两点．‎ 故∠B，∠D为同弧所对的两个圆周角．‎ 所以∠B＝∠D.因此∠OCB＝∠D.‎ 圆的切线性质与判定、弦切角定理 ‎　如图705，AB是⊙O的直径，AC是⊙O的切线，BC交⊙O于点E.‎ 图705‎ ‎(1)若D为AC的中点，证明：DE是⊙O的切线；‎ ‎(2)若OA＝CE，求∠ACB的大小. 【导学号：62172366】‎ ‎[解]　(1)证明：如图，连结AE，由已知得AE⊥BC，AC⊥AB.‎ 在Rt△AEC中，由已知得DE＝DC，故∠DEC＝∠DCE.‎ 连结OE，则∠OBE＝∠OEB.‎ 又∠ACB＋∠ABC＝90°，‎ 所以∠DEC＋∠OEB＝90°，‎ 故∠OED＝90°，即DE是⊙O的切线．‎ ‎(2)设CE＝1，AE＝x.‎ 由已知得AB＝2，BE＝.‎ 由射影定理可得AE2＝CE·BE，‎ 即x2＝，即x4＋x2－12＝0.‎ 解得x＝，所以∠ACB＝60°.‎ ‎[规律方法]　1.圆周角定理及其推论与弦切角定理及其推论多用于推出角的关系，从而证明三角形全等或相似，可求线段或角的大小．‎ ‎2．涉及圆的切线问题时要注意弦切角的转化；关于圆周上的点，常作直径(或半径)或向弦的(弧)两端作圆周角或弦切角．‎ ‎[变式训练1]　如图706，AB切⊙O于点B，直线AO交⊙O于D，E两点，BC⊥DE，垂足为C.‎ ‎(1)证明：∠CBD＝∠DBA；‎ ‎(2)若AD＝3DC，BC＝，求⊙O的直径．‎ 图706‎ ‎[解]　(1)证明：因为DE为⊙O直径，‎ 则∠BED＋∠EDB＝90°.‎ 又BC⊥DE，所以∠CBD＋∠EDB＝90°，‎ 从而∠CBD＝∠BED.‎ 又AB切⊙O于点B，得∠DBA＝∠BED，‎ 所以∠CBD＝∠DBA.‎ ‎(2)由(1)知BD平分∠CBA，则＝＝3.‎ 又BC＝，从而AB＝3，‎ 所以AC＝＝4，所以AD＝3.‎ 由切割线定理得AB2＝AD·AE，‎ 即AE＝＝6，‎ 故DE＝AE－AD＝3，即⊙O的直径为3.‎ 圆内接四边形及圆周角定理 ‎　(2016·全国卷Ⅱ)如图707，在正方形ABCD中，E，G分别在边DA，DC上(不与端点重合)，且DE＝DG，过D点作DF⊥CE，垂足为F.‎ ‎(1)证明：B，C，G，F四点共圆；‎ ‎(2)若AB＝1，E为DA的中点，求四边形BCGF的面积．‎ 图707‎ ‎[解]　(1)证明：因为DF⊥EC，‎ 所以△DEF∽△CDF，‎ 则有∠GDF＝∠DEF＝∠FCB，‎ ＝＝，‎ 所以△DGF∽△CBF，‎ 由此可得∠DGF＝∠CBF.‎ 因此∠CGF＋∠CBF＝180°，所以B，C，G，F四点共圆．‎ ‎(2)由B，C，G，F四点共圆，CG⊥CB知FG⊥FB.‎ 连结GB.由G为Rt△DFC斜边CD的中点，知GF＝GC，故Rt△BCG≌Rt△BFG，因此，四边形BCGF的面积S是△GCB面积S△GCB的2倍，‎ 即S＝2S△GCB＝2×××1＝.‎ ‎[规律方法]　1.判断四点共圆的步骤 ‎(1)观察几何图形，找到一对对角或一外角与其内对角；‎ ‎(2)判断四边形的一对对角的和是否为180°或判断四边形一外角与其内对角是否相等；‎ ‎(3)下结论．‎ ‎2．解决有关三角形与圆的试题，关键是正确处理角与边之间的关系，通过相应的条件与定理建立有关角之间或边之间的关系式，进而达到求解的目的．‎ ‎[变式训练2]　(2017·苏州市期中)如图708，AB是圆O的直径，弦BD，CA的延长线相交于点E，过E作BA的延长线的垂线，垂足为F.求证：AB2＝BE·BD－AE·AC.‎ 图708‎ ‎ [证明]　连结AD，BC，‎ ‎∵AB为圆的直径，‎ ‎∴∠ADB＝90°，‎ 又EF⊥AB，∠AFE＝90°，‎ 则A，D，E，F四点共圆，‎ ‎∴BD·BE＝BA·BF，‎ 又△ABC∽△AEF，‎ ‎∴＝，即AB·AF＝AE·AC.‎ ‎∴BE·BD－AE·AC＝BA·BF－AB·AF＝AB·(BF－AF)＝AB2.‎ 即AB2＝BE·BD－AE·AC.‎ 与圆有关的比例线段 ‎　如图709，正方形ABCD的边长为2，以A为圆心，DA为半径的圆弧与以BC为直径的半圆O交于点F，连结BF并延长交CD于点E.‎ ‎(1)求证：E为CD的中点；‎ ‎(2)求EF·FB的值. 【导学号：62172367】‎ 图709‎ ‎[解]　(1)证明：由题可知是以A为圆心，DA为半径作的圆弧，而四边形ABCD为正方形，‎ ‎∴ED为圆A的切线，‎ 依据切割线定理得ED2＝EF·EB，‎ 又圆O以BC为直径，∴EC是圆O的切线，‎ 同样依据切割线定理得EC2＝EF·EB，‎ 故EC＝ED，‎ ‎∴E为CD的中点．‎ ‎(2)连结CF，‎ ‎∵BC为圆O的直径，‎ ‎∴CF⊥BF，‎ 由S△BCE＝BC×CE＝BE×CF，‎ 得CF＝＝.‎ 在Rt△BCE中，由射影定理得 EF·FB＝CF2＝.‎ ‎[规律方法]　解决与圆有关的成比例线段问题的两种思路：‎ ‎1．直接应用相交弦、切割线定理及其推论．‎ ‎2．当比例式(等积式)中的线段分别在两个三角形中时，可转化为证明三角形相似，一般思路为“相似三角形→比例式→等积式”．在证明中有时还要借助中间比来代换，解题时应灵活把握．‎ ‎[变式训练3]　如图7010，P是⊙O外一点，PA是切线，A为切点，割线PBC与⊙O相交于点B，C，PC＝2PA，D为PC的中点，AD的延长线交⊙O于点E.‎ 证明：(1)BE＝EC；‎ ‎(2)AD·DE＝2PB2.‎ 图7010‎ ‎[证明]　(1)连结AB，AC，由题设知PA＝PD，故∠PAD＝∠PDA.‎ 因为∠PDA＝∠DAC＋∠DCA，∠PAD＝∠BAD＋∠PAB，∠DCA＝∠PAB，‎ 所以∠DAC＝∠BAE，‎ 从而＝.因此BE＝EC.‎ ‎(2)由切割线定理得PA2＝PB·PC.‎ 因为PA＝PD＝DC，所以DC＝2PB，BD＝PB.‎ 由相交弦定理得AD·DE＝BD·DC，‎ 所以AD·DE＝2PB2.‎ ‎[思想与方法]‎ ‎1．切点与圆心的连线与圆的切线垂直；过切点且与圆的切线垂直的直线过圆心．‎ ‎2．证明四点共圆的主要方法 ‎(1)圆内接四边形的判定定理．‎ ‎(2)圆内接四边形判定定理的推论．‎ ‎3．弦切角定理与圆周角定理是证明角相等的重要依据，解题时应根据需要添加辅助线构造所需要的角．‎ ‎[易错与防范]‎ ‎1．圆内接四边形的性质易得到相等的角，进而为得到三角形相似创造了条件．‎ ‎2．与圆有关的比例线段紧紧抓住两点：(1)切割线定理、相交弦定理；(2)利用圆内接四边形性质和三角形相似．‎ 课时分层训练(十四)‎ A组　基础达标 ‎(建议用时：30分钟)‎ ‎1．如图7011，在△ABC中，AB＝AC，△ABC的外接圆⊙O的弦AE交BC于点D.‎ 图7011‎ 求证：△ABD∽△AEB.‎ ‎[证明]　因为AB＝AC.‎ 所以∠ABD＝∠C.‎ 又⊙O是三角形ABC的外接圆，‎ 所以∠E＝∠C，从而∠ABD＝∠E.‎ 又∠BAE＝∠BAD.‎ 故△ABD∽△AEB.‎ ‎2．(2017·泰州模拟)如图7012，AB和BC分别与圆O相切于点D，C，AC经过圆心O，且BC＝2OC.‎ 图7012‎ 求证：AC＝2AD. 【导学号：62172368】‎ ‎[证明]　连结OD.因为AB和BC分别与圆O相切于点D，C，‎ 所以∠ADO＝∠ACB＝90°.‎ 又因为∠A＝∠A，‎ 所以Rt△ADO∽Rt△ACB，‎ 所以＝.‎ 又BC＝2OC＝2OD，‎ 故AC＝2AD.‎ ‎3．如图7013，圆O的弦AB，CD相交于点E，过点A作圆O的切线与DC的延长线交于点P，若PA＝6，AE＝9，PC＝3，CE∶ED＝2∶1，求BE的长．‎ 图7013‎ ‎[解]　由切割线定理，得PA2＝PC·PD.‎ 因此PD＝＝＝12.‎ 又PC＝3，所以CD＝PD－PC＝9.‎ 由于CE∶ED＝2∶1，‎ 因此CE＝6，ED＝3.‎ 由相交弦定理，AE·EB＝CE·ED，‎ 所以BE＝＝＝2.‎ ‎4．如图7014，在⊙O中，相交于点E的两弦AB，CD的中点分别是M，N，直线MO与直线CD相交于点F.证明：‎ 图7014‎ ‎(1)∠MEN＋∠NOM＝180°；‎ ‎(2)FE·FN＝FM·FO. 【导学号：62172369】‎ ‎[证明]　(1)如图所示，因为点M，N分别是弦AB，CD的中点，‎ 所以OM⊥AB，ON⊥CD，‎ 则∠OME＝90°，∠ENO＝90°，‎ 因此∠OME＋∠ONE＝180°.‎ 又四边形的内角和等于360°，‎ 故∠MEN＋∠NOM＝180°.‎ ‎(2)由(1)知，点O，M，E，N四点共圆．‎ 由割线定理，得FE·FN＝FM·FO.‎ B组　能力提升 ‎(建议用时：15分钟)‎ ‎1．如图7015，设AB为⊙O的任一条不与直线l垂直的直径，P是⊙O与l的公共点，AC⊥l，BD⊥l，垂足分别为C，D，且PC＝PD.‎ 图7015‎ ‎(1)求证：l是⊙O的切线；‎ ‎(2)若⊙O的半径OA＝5，AC＝4，求CD的长．‎ ‎[解]　(1)证明：连结OP，∵AC⊥l，BD⊥l，‎ ‎∴AC∥BD.‎ 又OA＝OB，PC＝PD，‎ ‎∴OP∥BD，从而OP⊥l.‎ ‎∵点P在⊙O上，‎ ‎∴l是⊙O的切线．‎ ‎(2)由(1)可得OP＝(AC＋BD)，‎ ‎∴BD＝2OP－AC＝10－4＝6.‎ 过点A作AE⊥BD，垂足为E，则 BE＝BD－AC＝6－4＝2.‎ ‎∴在Rt△ABE中，AE＝＝＝4，‎ ‎∴CD＝4.‎ ‎2．(2016·全国卷Ⅰ)如图7016，△OAB是等腰三角形，∠AOB＝120°，以O为圆心，OA为半径作圆．‎ 图7016‎ ‎(1)证明：直线AB与⊙O相切；‎ ‎(2)点C，D在⊙O上，且A，B，C，D四点共圆，证明：AB∥CD.‎ ‎[证明]　(1)设E是AB的中点，连结OE.‎ 因为OA＝OB，∠AOB＝120°，‎ 所以OE⊥AB，∠AOE＝60°.‎ 在Rt△AOE中，OE＝AO，即O到直线AB的距离等于⊙O的半径，所以直线AB与⊙O相切．‎ ‎(2)因为OA＝2OD，‎ 所以O不是A，B，C，D四点所在圆的圆心．‎ 设O′是A，B，C，D四点所在圆的圆心，作直线OO′.‎ 由已知得O在线段AB的垂直平分线上，‎ 又O′在线段AB的垂直平分线上，所以OO′⊥AB.‎ 同理可证，OO′⊥CD，所以AB∥CD.‎ ‎3．如图7017，圆内接四边形ABCD的边BC与AD的延长线交于点E，点F在BA的延长线上．‎ 图7017‎ ‎(1)若EF∥CD，证明：EF2＝FA·FB；‎ ‎(2)若EB＝3EC，EA＝2ED，求的值．‎ ‎[解]　(1)证明：因为四边形ABCD内接于圆，所以∠B＝∠CDE.‎ 又EF∥CD，所以∠CDE＝∠FEA，‎ 因此，∠B＝∠FEA.‎ 而∠F为公共角，‎ 所以△FAE∽△FEB，‎ 于是，＝，即EF2＝FA·FB.‎ ‎(2)由割线定理，得ED·EA＝EC·EB，即ED·2ED＝EC·3EC，‎ 所以＝，即＝.‎ 因为∠B＝∠CDE，∠CED是公共角，所以△ECD∽△EAB，‎ 于是，＝＝＝·＝.‎ ‎4．(2016·全国卷Ⅲ)如图7018，⊙O中的中点为P，弦PC，PD分别交AB于E，F两点．‎ 图7018‎ ‎(1)若∠PFB＝2∠PCD，求∠PCD的大小；‎ ‎(2)若EC的垂直平分线与FD的垂直平分线交于点G，证明OG⊥CD.‎ ‎[解]　(1)如图，连结PB，BC，‎ 则∠BFD＝∠PBA＋∠BPD，‎ ‎∠PCD＝∠PCB＋∠BCD.‎ 因为＝，‎ 所以∠PBA＝∠PCB.‎ 又∠BPD＝∠BCD，‎ 所以∠BFD＝∠PCD.‎ 又∠PFB＋∠BFD＝180°，∠PFB＝2∠PCD，‎ 所以3∠PCD＝180°，‎ 因此∠PCD＝60°.‎ ‎(2)证明：因为∠PCD＝∠BFD，‎ 所以∠EFD＋∠PCD＝180°，‎ 由此知C，D，F，E四点共圆，其圆心既在CE的垂直平分线上，又在DF的垂直平分线上，‎ 故G就是过C，D，F，E四点的圆的圆心，‎ 所以G在CD的垂直平分线上．‎ 又O也在CD的垂直平分线上，因此OG⊥CD.‎