2015年高考数学（文科）真题分类汇编G单元 立体几何 37页

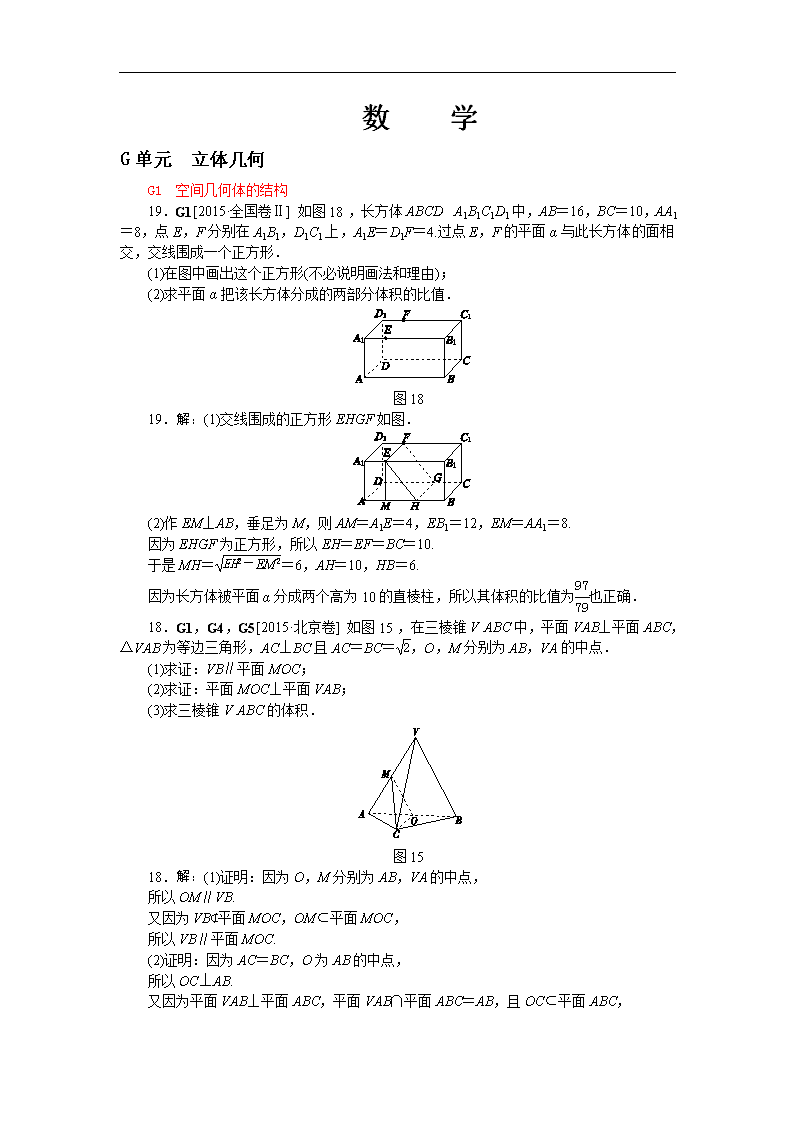
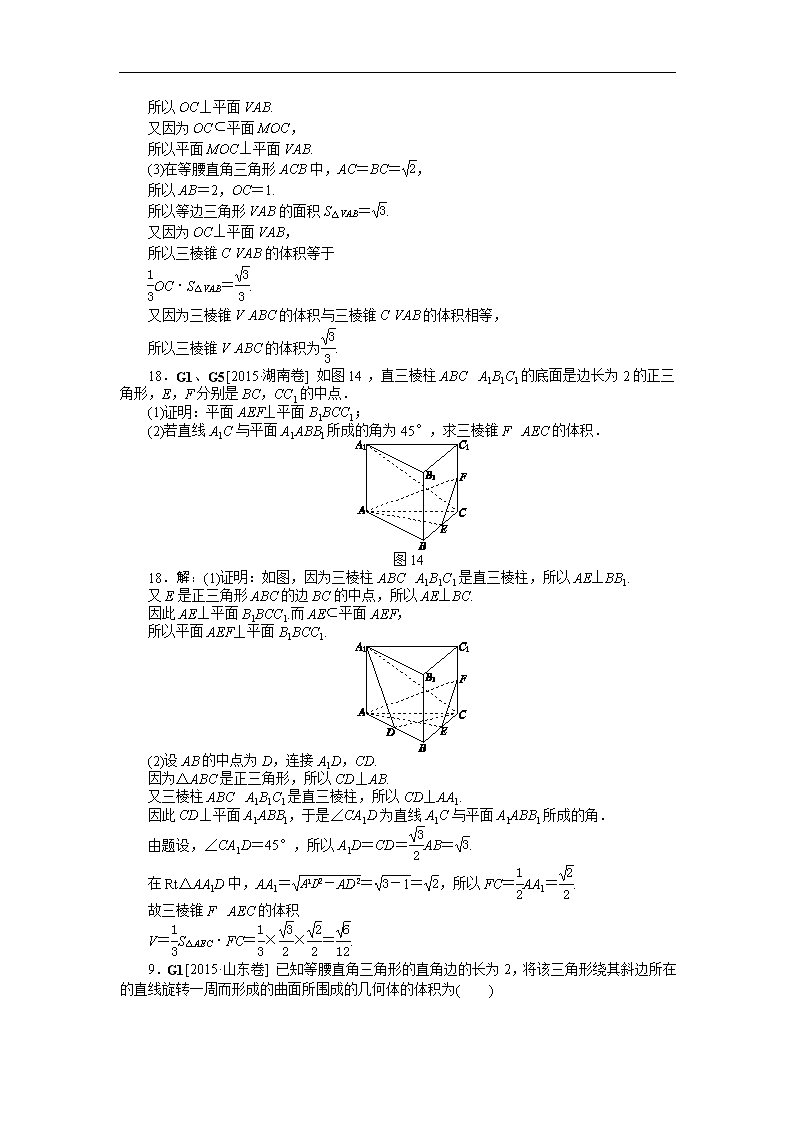
‎ 数 学 G单元 立体几何 ‎ G1 空间几何体的结构 ‎ ‎19．G1[2015·全国卷Ⅱ] 如图18，长方体ABCD A1B‎1C1D1中，AB＝16，BC＝10，AA1＝8，点E，F分别在A1B1，D‎1C1上，A1E＝D‎1F＝4.过点E，F的平面α与此长方体的面相交，交线围成一个正方形．‎ ‎(1)在图中画出这个正方形(不必说明画法和理由)；‎ ‎(2)求平面α把该长方体分成的两部分体积的比值．‎ 图18‎ ‎19．解：(1)交线围成的正方形EHGF如图．‎ ‎(2)作EM⊥AB，垂足为M，则AM＝A1E＝4，EB1＝12，EM＝AA1＝8.‎ 因为EHGF为正方形，所以EH＝EF＝BC＝10.‎ 于是MH＝＝6，AH＝10，HB＝6.‎ 因为长方体被平面α分成两个高为10的直棱柱，所以其体积的比值为也正确．‎ ‎18．G1，G4，G5[2015·北京卷] 如图15，在三棱锥VABC中，平面VAB⊥平面ABC，△VAB为等边三角形，AC⊥BC且AC＝BC＝，O，M分别为AB，VA的中点．‎ ‎(1)求证：VB∥平面MOC；‎ ‎(2)求证：平面MOC⊥平面VAB；‎ ‎(3)求三棱锥VABC的体积．‎ 图15‎ ‎18．解：(1)证明：因为O，M分别为AB，VA的中点，‎ 所以OM∥VB.‎ 又因为VB⊄平面MOC，OM⊂平面MOC，‎ 所以VB∥平面MOC.‎ ‎(2)证明：因为AC＝BC，O为AB的中点，‎ 所以OC⊥AB.‎ 又因为平面VAB⊥平面ABC，平面VAB∩平面ABC＝AB，且OC⊂平面ABC，‎ 所以OC⊥平面VAB.‎ 又因为OC⊂平面MOC，‎ 所以平面MOC⊥平面VAB.‎ ‎(3)在等腰直角三角形ACB中，AC＝BC＝，‎ 所以AB＝2，OC＝1.‎ 所以等边三角形VAB的面积S△VAB＝.‎ 又因为OC⊥平面VAB，‎ 所以三棱锥CVAB的体积等于 OC·S△VAB＝.‎ 又因为三棱锥VABC的体积与三棱锥CVAB的体积相等，‎ 所以三棱锥VABC的体积为.‎ ‎18．G1、G5[2015·湖南卷] 如图14，直三棱柱ABC A1B‎1C1的底面是边长为2的正三角形，E，F分别是BC，CC1的中点．‎ ‎(1)证明：平面AEF⊥平面B1BCC1；‎ ‎(2)若直线A‎1C与平面A1ABB1所成的角为45°，求三棱锥F AEC的体积．‎ 图14‎ ‎18．解：(1)证明：如图，因为三棱柱ABC A1B‎1C1是直三棱柱，所以AE⊥BB1.‎ 又E是正三角形ABC的边BC的中点，所以AE⊥BC.‎ 因此AE⊥平面B1BCC1.而AE⊂平面AEF，‎ 所以平面AEF⊥平面B1BCC1.‎ ‎(2)设AB的中点为D，连接A1D，CD.‎ 因为△ABC是正三角形，所以CD⊥AB.‎ 又三棱柱ABC A1B‎1C1是直三棱柱，所以CD⊥AA1.‎ 因此CD⊥平面A1ABB1，于是∠CA1D为直线A‎1C与平面A1ABB1所成的角．‎ 由题设，∠CA1D＝45°，所以A1D＝CD＝AB＝.‎ 在Rt△AA1D中，AA1＝＝＝，所以FC＝AA1＝.‎ 故三棱锥F AEC的体积 V＝S△AEC·FC＝××＝.‎ ‎9．G1[2015·山东卷] 已知等腰直角三角形的直角边的长为2，将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为(　　)‎ A. B. C．2π D．4π ‎9．B　[解析] 由条件知该直角三角形的斜边长为2，斜边上的高为，故围成的几何体的体积为2××π×()2×＝.‎ ‎18．G1，G4，G5[2015·四川卷] 一个正方体的平面展开图及该正方体的直观图的示意图如图12所示．‎ ‎(1)请将字母F，G，H标记在正方体相应的顶点处(不需说明理由)；‎ ‎(2)判断平面BEG与平面ACH的位置关系，并证明你的结论；‎ ‎(3)证明：直线DF⊥平面BEG.‎ 图12‎ ‎18．解：(1)点F，G，H的位置如图所示．‎ ‎(2)平面BEG∥平面ACH.证明如下：‎ 因为ABCDEFGH为正方体，所以BC∥FG，BC＝FG，‎ 又FG∥EH，FG＝EH，所以BC∥EH，BC＝EH，‎ 于是BCHE为平行四边形，‎ 所以BE∥CH.‎ 又CH⊂平面ACH，BE⊄平面ACH，‎ 所以BE∥平面ACH.‎ 同理BG∥平面ACH.‎ 又BE∩BG＝B，‎ 所以平面BEG∥平面ACH.‎ ‎(3)证明：连接FH.‎ 因为ABCDEFGH为正方体，所以DH⊥平面EFGH.‎ 因为EG⊂平面EFGH，所以DH⊥EG，‎ 又EG⊥FH，EG∩FH＝O，‎ 所以EG⊥平面BFHD.‎ 又DF⊂平面BFHD，所以DF⊥EG.‎ 同理DF⊥BG.‎ 又EG∩BG＝G，‎ 所以DF⊥平面BEG.‎ ‎10．G1、G2[2015·天津卷] 一个几何体的三视图如图13所示(单位：m)，则该几何体的体积为________m3.‎ 图13‎ ‎10.π　[解析] 根据三视图可知，该几何体是圆柱与两个圆锥的组合体，其体积V＝π×12×2＋2××π×12×1＝π(m3)．‎ G2 空间几何体的三视图和直观图 ‎9．G2[2015·安徽卷] 一个四面体的三视图如图12所示，则该四面体的表面积是(　　)‎ 图12‎ A．1＋ B．1＋2 C．2＋ D．2 ‎9．C　[解析] 四面体的直观图如图所示，设O是AC的中点，则OP＝OB＝1，因此PB＝，于是S△PAB＝S△PBC＝×()2＝，S△PAC＝S△ABC＝×2×1＝1，故四面体的表面积S＝2×1＋2×＝2＋.‎ ‎11．G2[2015·全国卷Ⅰ] 圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体，该几何体三视图中的正视图和俯视图如图14所示．若该几何体的表面积为16＋20π，则r＝(　　)‎ 图14‎ A．1 B．2‎ C．4 D．8‎ ‎11．B　[解析] 由三视图可知，此组合体的前半部分是一个底面半径为r，高为2r的半圆柱(水平放置)，后半部分是一个半径为r的半球，其中半圆柱的一个底面与半球的半个圆面重合，所以此几何体的表面积为2r·2r＋πr2＋πr2＋πr·2r＋2πr2＝4r2＋5πr2＝16＋20π，解得r＝2.‎ ‎6．G2[2015·全国卷Ⅱ] 一个正方体被一个平面截去一部分后，剩余部分的三视图如图12，则截去部分体积与剩余部分体积的比值为(　　)‎ 图12‎ A. B. C. D. ‎6．D　[解析] 由剩余部分的三视图可知，正方体被截去一个三棱锥，剩余部分如图所示，设正方体的棱长为a，则被截去的三棱锥的体积为×a2×a＝a3，而正方体的体积为a3，所以截去部分体积与剩余部分体积的比值为.‎ ‎7．G2[2015·北京卷] 某四棱锥的三视图如图12所示，该四棱锥最长棱的棱长为(　　)‎ 图12‎ A．1 B. C. D．2‎ ‎7．C　[解析] 根据三视图可得，此四棱锥是底面是正方形，有一条侧棱和底面垂直的四棱锥，如图所示，所以最长棱的棱长为PC＝＝，故选C.‎ ‎9．G2[2015·福建卷] 某几何体的三视图如图13所示，则该几何体的表面积等于(　　)‎ 图13‎ A．8＋2 B．11＋2 C．14＋2 D．15‎ ‎9．B　[解析] 由三视图可知，该几何体是底面为直角梯形的直四棱柱，其表面积S＝(1＋1＋2＋)×2＋×(1＋2)×1×2＝11＋2 .‎ ‎10．G2、G7、K3[2015·湖南卷] 某工件的三视图如图13所示，现将该工件通过切削，加工成一个体积尽可能大的正方体新工件，并使新工件的一个面落在原工件的一个面内，则原工件材料的利用率为(材料利用率＝)(　　)‎ 图13‎ A. B. C. D. ‎10．A　[解析] 由三视图知，原工件是底面半径为1，母线长为3的圆锥．‎ 设新正方体工件的棱长为x，借助轴截面，由三角形相似可得，＝，得x＝，故V正＝x3＝，又V圆锥＝π×12×＝，故利用率为＝，选A.‎ ‎5．G2[2015·陕西卷] 一个几何体的三视图如图12所示，则该几何体的表面积为(　　)‎ 图12‎ A．3π B．4π C．2π＋4 D．3π＋4‎ ‎5．D　[解析] 该几何体是底面半径为1、高为2的圆柱被其轴截面截开的半个圆柱，其表面积为×2π×1×2＋2××π×12＋2×2＝3π＋4.‎ ‎14．G2，G7[2015·四川卷] 在三棱柱ABCA1B‎1C1中，∠BAC＝90°，其正视图和侧视图都是边长为1的正方形，俯视图是直角边的长为1的等腰直角三角形，设点M，N，P分别是棱AB，BC，B‎1C1的中点，则三棱锥PA1MN的体积是________．‎ ‎14.　[解析] 由题意知，三棱柱的底面是直角边长为1的等腰直角三角形，棱柱的高为1且该棱柱为直三棱柱，其底面积为，三棱锥A1PMN的底面积是××1，高为，故三棱锥PA1MN的体积为××＝.‎ ‎10．G1、G2[2015·天津卷] 一个几何体的三视图如图13所示(单位：m)，则该几何体的体积为________m3.‎ 图13‎ ‎10.π　[解析] 根据三视图可知，该几何体是圆柱与两个圆锥的组合体，其体积V＝π×12×2＋2××π×12×1＝π(m3)．‎ ‎2．G2[2015·浙江卷] 某几何体的三视图如图11所示(单位：cm)，则该几何体的体积是(　　)‎ 图11‎ A．‎8 cm3 B．‎12 cm3‎ C. cm3 D. cm3‎ ‎2．C　[解析] 该几何体为一个正方体和一个四棱锥的组合体，故所求体积为23＋×2×2×2＝.‎ G3 平面的基本性质、空间两条直线 ‎6．G3[2015·广东卷] 若直线l1和l2是异面直线，l1在平面α内，l2在平面β内，l是平面α与平面β的交线，则下列命题正确的是(　　)‎ A．l与l1，l2都不相交 B．l与l1，l2都相交 C．l至多与l1，l2中的一条相交 D．l至少与l1，l2中的一条相交 ‎6．D　[解析] 若直线l1和l2是异面直线，l1在平面α内，l2在平面β内，l是平面α与平面β的交线，则l至少与l1，l2中的一条相交，故选D.‎ ‎5．A2、G3[2015·湖北卷] l1，l2表示空间中的两条直线，若p：l1，l2是异面直线；q：l1，l2不相交，则(　　)‎ A．p是q的充分条件，但不是q的必要条件 B．p是q的必要条件，但不是q的充分条件 C．p是q的充分必要条件 D．p既不是q的充分条件，也不是q的必要条件 ‎5．A　[解析] 由l1，l2是异面直线，可得l1，l2不相交，所以p⇒q；由l1，l2不相交，可得l1，l2是异面直线或l1∥l2，所以q⇒/ p．所以p是q的充分条件，但不是q的必要条件．故选A.‎ G4 空间中的平行关系 ‎ ‎18．G4，G5，G11[2015·广东卷] 如图13，三角形PDC所在的平面与长方形ABCD所在的平面垂直，PD＝PC＝4，AB＝6，BC＝3.‎ ‎(1)证明：BC∥平面PDA；‎ ‎(2)证明：BC⊥PD；‎ ‎(3)求点C到平面PDA的距离．‎ 图13‎ ‎18．G1，G4，G5[2015·北京卷] 如图15，在三棱锥VABC中，平面VAB⊥平面ABC，△VAB为等边三角形，AC⊥BC且AC＝BC＝，O，M分别为AB，VA的中点．‎ ‎(1)求证：VB∥平面MOC；‎ ‎(2)求证：平面MOC⊥平面VAB；‎ ‎(3)求三棱锥VABC的体积．‎ 图15‎ ‎18．解：(1)证明：因为O，M分别为AB，VA的中点，‎ 所以OM∥VB.‎ 又因为VB⊄平面MOC，OM⊂平面MOC，‎ 所以VB∥平面MOC.‎ ‎(2)证明：因为AC＝BC，O为AB的中点，‎ 所以OC⊥AB.‎ 又因为平面VAB⊥平面ABC，平面VAB∩平面ABC＝AB，且OC⊂平面ABC，‎ 所以OC⊥平面VAB.‎ 又因为OC⊂平面MOC，‎ 所以平面MOC⊥平面VAB.‎ ‎(3)在等腰直角三角形ACB中，AC＝BC＝，‎ 所以AB＝2，OC＝1.‎ 所以等边三角形VAB的面积S△VAB＝.‎ 又因为OC⊥平面VAB，‎ 所以三棱锥CVAB的体积等于 OC·S△VAB＝.‎ 又因为三棱锥VABC的体积与三棱锥CVAB的体积相等，‎ 所以三棱锥VABC的体积为.‎ ‎18．G4、G5[2015·山东卷] 如图13，三棱台DEF ABC中，AB＝2DE，G，H分别为AC，BC的中点．‎ ‎(1)求证：BD∥平面FGH；‎ ‎(2)若CF⊥BC，AB⊥BC，求证：平面BCD⊥平面EGH.‎ ‎18．证明：(1)证法一：如图，连接DG，CD，设CD∩GF＝M，连接MH.‎ 在三棱台DEF ABC中，‎ AB＝2DE，G为AC的中点，‎ 可得DF∥GC，DF＝GC，‎ 所以四边形DFCG为平行四边形，‎ 则M为CD的中点．又H为BC的中点，‎ 所以HM∥BD.‎ 又HM⊂平面FGH，BD⊄平面FGH，‎ 所以BD∥平面FGH.‎ 证法二：在三棱台DEF ABC中，‎ 由BC＝2EF，H为BC的中点，‎ 可得BH∥EF，BH＝EF，‎ 所以四边形HBEF为平行四边形，‎ 可得BE∥HF.‎ 在△ABC中，G为AC的中点，H为BC的中点，‎ 所以GH∥AB.‎ 又GH∩HF＝H，AB∩BE＝B，‎ 所以平面FGH∥平面ABED.‎ 因为BD⊂平面ABED，‎ 所以BD∥平面FGH.‎ ‎(2)如图，连接HE，GE.‎ 因为G，H分别为AC，BC的中点，‎ 所以GH∥AB.‎ 由AB⊥BC，得GH⊥BC，‎ 又H为BC的中点，‎ 所以EF∥HC，EF＝HC，‎ 因此四边形EFCH是平行四边形，‎ 所以CF∥HE.‎ 又CF⊥BC，所以HE⊥BC.‎ 又HE，GH⊂平面EGH，HE∩GH＝H，‎ 所以BC⊥平面EGH.‎ 又BC⊂平面BCD，‎ 所以平面BCD⊥平面EGH.‎ ‎18．G1，G4，G5[2015·四川卷] 一个正方体的平面展开图及该正方体的直观图的示意图如图12所示．‎ ‎(1)请将字母F，G，H标记在正方体相应的顶点处(不需说明理由)；‎ ‎(2)判断平面BEG与平面ACH的位置关系，并证明你的结论；‎ ‎(3)证明：直线DF⊥平面BEG.‎ 图12‎ ‎18．解：(1)点F，G，H的位置如图所示．‎ ‎(2)平面BEG∥平面ACH.证明如下：‎ 因为ABCDEFGH为正方体，所以BC∥FG，BC＝FG，‎ 又FG∥EH，FG＝EH，所以BC∥EH，BC＝EH，‎ 于是BCHE为平行四边形，‎ 所以BE∥CH.‎ 又CH⊂平面ACH，BE⊄平面ACH，‎ 所以BE∥平面ACH.‎ 同理BG∥平面ACH.‎ 又BE∩BG＝B，‎ 所以平面BEG∥平面ACH.‎ ‎(3)证明：连接FH.‎ 因为ABCDEFGH为正方体，所以DH⊥平面EFGH.‎ 因为EG⊂平面EFGH，所以DH⊥EG，‎ 又EG⊥FH，EG∩FH＝O，‎ 所以EG⊥平面BFHD.‎ 又DF⊂平面BFHD，所以DF⊥EG.‎ 同理DF⊥BG.‎ 又EG∩BG＝G，‎ 所以DF⊥平面BEG.‎ ‎17．G4、G5、G11[2015·天津卷] 如图14，已知AA1⊥平面ABC，BB1∥AA1，AB＝AC ‎＝3，BC＝2，AA1＝，BB1＝2，点E和F分别为BC和A‎1C中点．‎ ‎(1)求证：EF∥平面A1B1BA；‎ ‎(2)求证：平面AEA1⊥平面BCB1；‎ ‎(3)求直线A1B1与平面BCB1所成角的大小．‎ 图14‎ ‎17．解：(1)证明：如图所示，连接A1B.在△A1BC中，因为E和F分别是BC和A‎1C的中点，所以EF∥BA1.又因为EF⊄平面A1B1BA，所以EF∥平面A1B1BA.‎ ‎(2)证明：因为AB＝AC，E为BC的中点，所以AE⊥BC.因为AA1⊥平面ABC，BB1∥AA1，所以BB1⊥平面ABC，从而BB1⊥AE.又因为BC∩BB1＝B，所以AE⊥平面BCB1.又因为AE⊂平面AEA1，所以平面AEA1⊥平面BCB1.‎ ‎(3)取BB1的中点M和B‎1C的中点N，连接A‎1M，A1N，NE.因为N和E分别为B‎1C和BC的中点，所以NE∥B1B，NE＝B1B，故NE∥A‎1A，且NE＝A‎1A，所以A1N∥AE，且A1N＝AE.又因为AE⊥平面BCB1，所以A1N⊥平面BCB1，从而∠A1B1N为直线A1B1与平面BCB1所成的角．‎ 在△ABC中，可得AE＝2，所以A1N＝AE＝2.‎ 因为BM∥AA1，BM＝AA1，所以A‎1M∥AB，A‎1M＝AB, 又由AB⊥BB1，得A‎1M⊥BB1.‎ 在Rt△A1MB1中，可得A1B1＝＝4.‎ 在Rt△A1NB1中，sin∠A1B1N＝＝，因此∠A1B1N＝30°，‎ 所以直线A1B1与平面BCB1所成的角为30°.‎ ‎4．G4，G5[2015·浙江卷] 设α，β是两个不同的平面，l，m是两条不同的直线，且l⊂α，m⊂β(　　)‎ A．若l⊥β，则α⊥β B．若α⊥β，则l⊥m C．若l∥β，则α∥β D．若α∥β，则l∥m ‎4．A　[解析] 由两平面垂直的判定定理知，A正确；对于B，直线l，m相交、平行、异面都有可能，故不正确；对于C，要求α内两条相交直线都平行于β，才能推出α∥β，故不正确；对于D，l，m平行和异面都有可能，故不正确．‎ ‎16．G4、G5[2015·江苏卷] 如图12，在直三棱柱ABC A1B‎1C1中，已知AC⊥BC，BC＝CC1，设AB1的中点为D，B‎1C∩BC1＝E.‎ 求证：(1)DE∥平面AA‎1C1C；‎ ‎(2)BC1⊥AB1.‎ 图12‎ ‎16．证明：(1)由题意知，E为B‎1C的中点，‎ 又D为AB1的中点，因此DE∥AC.‎ 又因为DE⊄平面AA‎1C1C，AC⊂平面AA‎1C1C，‎ 所以DE∥平面AA‎1C1C.‎ ‎(2)因为三棱柱ABC A1B‎1C1是直三棱柱，‎ 所以CC1⊥平面ABC.‎ 因为AC⊂平面ABC，所以AC⊥CC1.‎ 又因为AC⊥BC，CC1⊂平面BCC1B1，‎ BC⊂平面BCC1B1，BC∩CC1＝C，‎ 所以AC⊥平面BCC1B1.‎ 又因为BC1⊂平面BCC1B1，所以BC1⊥AC.‎ 因为BC＝CC1，所以矩形BCC1B1是正方形，因此BC1⊥B‎1C.‎ 因为AC，B‎1C⊂平面B‎1AC，AC∩B‎1C＝C，所以BC1⊥平面B‎1AC.‎ 又因为AB1⊂平面B‎1AC，所以BC1⊥AB1.‎ G5 空间中的垂直关系 ‎18．G4，G5，G11[2015·广东卷] 如图13，三角形PDC所在的平面与长方形ABCD所在的平面垂直，PD＝PC＝4，AB＝6，BC＝3.‎ ‎(1)证明：BC∥平面PDA；‎ ‎(2)证明：BC⊥PD；‎ ‎(3)求点C到平面PDA的距离．‎ 图13‎ ‎20．G5、G12[2015·湖北卷] 《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．‎ 在如图14所示的阳马P ABCD中，侧棱PD⊥底面ABCD，且PD＝CD，点E是PC的中点，连接DE，BD，BE.‎ ‎(1)证明：DE⊥平面PBC.试判断四面体EBCD是否为鳖臑，若是，写出其每个面的直角(只需写出结论)；若不是，请说明理由．‎ ‎(2)记阳马P ABCD的体积为V1，四面体EBCD的体积为V2，求的值．‎ 图14‎ ‎20．解：(1)证明：因为PD⊥底面ABCD，所以PD⊥BC.‎ 由底面ABCD为长方形，有BC⊥CD，而PD∩CD＝D，‎ 所以BC⊥平面PCD.又DE⊂平面PCD，所以BC⊥DE.‎ 又因为PD＝CD，点E是PC的中点，所以DE⊥PC.‎ 而PC∩BC＝C，所以DE⊥平面PBC.‎ 由BC⊥平面PCD，DE⊥平面PBC，可知四面体EBCD的四个面都是直角三角形，‎ 即四面体EBCD是一个鳖臑，其四个面的直角分别是∠BCD，∠BCE，∠DEC，∠DEB.‎ ‎(2)由已知，PD是阳马P ABCD的高，所以V1＝S长方形ABCD·PD＝BC·CD·PD；‎ 由(1)知，DE是鳖臑D BCE的高，BC⊥CE，‎ 所以V2＝S△BCE·DE＝BC·CE·DE.‎ 在Rt△PDC中，因为PD＝CD，点E是PC的中点，所以DE＝CE＝CD.‎ 于是＝＝＝4.‎ ‎18．G5[2015·全国卷Ⅰ] 如图15，四边形ABCD为菱形，G为AC与BD的交点，BE⊥平面ABCD.‎ ‎(1)证明：平面AEC⊥平面BED；‎ ‎(2)若∠ABC＝120°，AE⊥EC, 三棱锥E ACD的体积为，求该三棱锥的侧面积．‎ 图15‎ ‎18．解：(1)证明：因为四边形ABCD为菱形，所以AC⊥BD.‎ 因为BE⊥平面ABCD，所以AC⊥BE，故AC⊥平面BED.‎ 又AC⊂平面AEC，所以平面AEC⊥平面BED.‎ ‎(2)设AB＝x，在菱形ABCD中，由∠ABC＝120°，可得AG＝GC＝x，GB＝GD＝.‎ 因为AE⊥EC，所以在Rt△AEC中，可得EG＝x.‎ 由BE⊥平面ABCD，知△EBG为直角三角形，可得BE＝x.‎ 由已知得，三棱锥E ACD的体积VE ACD＝×AC·GD·BE＝x3＝，‎ 故x＝2.从而可得AE＝EC＝ED＝，‎ 所以△EAC的面积为3，△EAD的面积与△ECD的面积均为.‎ 故三棱锥E ACD的侧面积为3＋2.‎ ‎18．G1，G4，G5[2015·北京卷] 如图15，在三棱锥VABC中，平面VAB⊥平面ABC，△VAB为等边三角形，AC⊥BC且AC＝BC＝，O，M分别为AB，VA的中点．‎ ‎(1)求证：VB∥平面MOC；‎ ‎(2)求证：平面MOC⊥平面VAB；‎ ‎(3)求三棱锥VABC的体积．‎ 图15‎ ‎18．解：(1)证明：因为O，M分别为AB，VA的中点，‎ 所以OM∥VB.‎ 又因为VB⊄平面MOC，OM⊂平面MOC，‎ 所以VB∥平面MOC.‎ ‎(2)证明：因为AC＝BC，O为AB的中点，‎ 所以OC⊥AB.‎ 又因为平面VAB⊥平面ABC，平面VAB∩平面ABC＝AB，且OC⊂平面ABC，‎ 所以OC⊥平面VAB.‎ 又因为OC⊂平面MOC，‎ 所以平面MOC⊥平面VAB.‎ ‎(3)在等腰直角三角形ACB中，AC＝BC＝，‎ 所以AB＝2，OC＝1.‎ 所以等边三角形VAB的面积S△VAB＝.‎ 又因为OC⊥平面VAB，‎ 所以三棱锥CVAB的体积等于 OC·S△VAB＝.‎ 又因为三棱锥VABC的体积与三棱锥CVAB的体积相等，‎ 所以三棱锥VABC的体积为.‎ ‎20．G5、G12[2015·福建卷] 如图15，AB是圆O的直径，点C是圆O上异于A，B的点，PO垂直于圆O所在的平面，且PO＝OB＝1.‎ ‎(1)若D为线段AC的中点，求证：AC⊥平面PDO；‎ ‎(2)求三棱锥PABC体积的最大值；‎ ‎(3)若BC＝，点E在线段PB上，求CE＋OE的最小值．‎ 图15‎ ‎20．解：方法一：(1)证明：在△AOC中，因为OA＝OC，D为AC的中点，‎ 所以AC⊥DO.‎ 又PO垂直于圆O所在的平面，‎ 所以PO⊥AC.‎ 因为DO∩PO＝O，DO⊂平面PDO，PO⊂平面PDO，‎ 所以AC⊥平面PDO.‎ ‎(2)因为点C在圆O上，‎ 所以当CO⊥AB时，C到AB的距离最大，且最大值为1.‎ 又AB＝2，所以△ABC面积的最大值为 ×2×1＝1.‎ 又因为三棱锥PABC的高PO＝1，‎ 故三棱锥PABC体积的最大值为×1×1＝.‎ ‎(3)在△POB中，PO＝OB＝1，∠POB＝90°，‎ 所以PB＝＝.‎ 同理PC＝，所以PB＝PC＝BC.‎ 在三棱锥PABC中，将侧面BCP绕PB旋转至平面BC′P, 使之与平面ABP共面，如图所示．‎ 当O，E，C′共线时，CE＋OE取得最小值．‎ 又因为OP＝OB，C′P＝C′B，‎ 所以OC′垂直平分PB，‎ 即E为PB中点．‎ 从而OC′＝OE＋EC′＝＋＝，‎ 亦即CE＋OE的最小值为.‎ 方法二：(1)(2)同方法一．‎ ‎(3)在△POB中，PO＝OB＝1，∠POB＝90°，‎ 所以∠OPB＝45°，PB＝＝.‎ 同理PC＝.‎ 所以PB＝PC＝BC，所以∠CPB＝60°.‎ 在三棱锥PABC中，将侧面BCP绕PB旋转至平面BC′P，使之与平面ABP共面，如图所示．‎ 当O，E，C′共线时，CE＋OE取得最小值．‎ 所以在△OC′P中，由余弦定理得，‎ OC′2＝1＋2－2×1××cos(45°＋60°)＝1＋2－2 ××－×＝2＋.‎ 从而OC′＝＝.‎ 所以CE＋OE的最小值为＋.‎ ‎18．G1、G5[2015·湖南卷] 如图14，直三棱柱ABC A1B‎1C1的底面是边长为2的正三角形，E，F分别是BC，CC1的中点．‎ ‎(1)证明：平面AEF⊥平面B1BCC1；‎ ‎(2)若直线A‎1C与平面A1ABB1所成的角为45°，求三棱锥F AEC的体积．‎ 图14‎ ‎18．解：(1)证明：如图，因为三棱柱ABC A1B‎1C1是直三棱柱，所以AE⊥BB1.‎ 又E是正三角形ABC的边BC的中点，所以AE⊥BC.‎ 因此AE⊥平面B1BCC1.而AE⊂平面AEF，‎ 所以平面AEF⊥平面B1BCC1.‎ ‎(2)设AB的中点为D，连接A1D，CD.‎ 因为△ABC是正三角形，所以CD⊥AB.‎ 又三棱柱ABC A1B‎1C1是直三棱柱，所以CD⊥AA1.‎ 因此CD⊥平面A1ABB1，于是∠CA1D为直线A‎1C与平面A1ABB1所成的角．‎ 由题设，∠CA1D＝45°，所以A1D＝CD＝AB＝.‎ 在Rt△AA1D中，AA1＝＝＝，所以FC＝AA1＝.‎ 故三棱锥F AEC的体积 V＝S△AEC·FC＝××＝.‎ ‎18．G4、G5[2015·山东卷] 如图13，三棱台DEF ABC中，AB＝2DE，G，H分别为AC，BC的中点．‎ ‎(1)求证：BD∥平面FGH；‎ ‎(2)若CF⊥BC，AB⊥BC，求证：平面BCD⊥平面EGH.‎ ‎18．证明：(1)证法一：如图，连接DG，CD，设CD∩GF＝M，连接MH.‎ 在三棱台DEF ABC中，‎ AB＝2DE，G为AC的中点，‎ 可得DF∥GC，DF＝GC，‎ 所以四边形DFCG为平行四边形，‎ 则M为CD的中点．又H为BC的中点，‎ 所以HM∥BD.‎ 又HM⊂平面FGH，BD⊄平面FGH，‎ 所以BD∥平面FGH.‎ 证法二：在三棱台DEF ABC中，‎ 由BC＝2EF，H为BC的中点，‎ 可得BH∥EF，BH＝EF，‎ 所以四边形HBEF为平行四边形，‎ 可得BE∥HF.‎ 在△ABC中，G为AC的中点，H为BC的中点，‎ 所以GH∥AB.‎ 又GH∩HF＝H，AB∩BE＝B，‎ 所以平面FGH∥平面ABED.‎ 因为BD⊂平面ABED，‎ 所以BD∥平面FGH.‎ ‎(2)如图，连接HE，GE.‎ 因为G，H分别为AC，BC的中点，‎ 所以GH∥AB.‎ 由AB⊥BC，得GH⊥BC，‎ 又H为BC的中点，‎ 所以EF∥HC，EF＝HC，‎ 因此四边形EFCH是平行四边形，‎ 所以CF∥HE.‎ 又CF⊥BC，所以HE⊥BC.‎ 又HE，GH⊂平面EGH，HE∩GH＝H，‎ 所以BC⊥平面EGH.‎ 又BC⊂平面BCD，‎ 所以平面BCD⊥平面EGH.‎ ‎18．G5[2015·陕西卷] 如图15(1)，在直角梯形ABCD中，AD∥BC，∠BAD＝，AB＝BC＝AD＝a，E是AD的中点，O是AC与BE的交点．将△ABE沿BE折起到图(2)中△A1BE的位置，得到四棱锥A1 BCDE.‎ ‎(1)证明：CD⊥平面A1OC；‎ ‎(2)当平面A1BE⊥平面BCDE时，四棱锥A1 BCDE的体积为36，求a的值．‎ ‎　　‎ 图15‎ ‎18．解：(1)证明：在图(1)中，‎ 因为AB＝BC＝AD＝a，E是AD的中点，‎ ‎∠BAD＝，所以BE⊥AC，‎ 即在图(2)中，BE⊥A1O，BE⊥OC，‎ 从而BE⊥平面A1OC.‎ 又CD∥BE，‎ 所以CD⊥平面A1OC.‎ ‎(2)由已知，平面A1BE⊥平面BCDE，‎ 且平面A1BE∩平面BCDE＝BE，‎ 又由(1)知，A1O⊥BE，‎ 所以A1O⊥平面BCDE，‎ 即A1O是四棱锥A1 BCDE的高．‎ 由图(1)知，A1O＝AB＝a，平行四边形BCDE的面积S＝BC·AB＝a2.‎ 从而四棱锥A1 BCDE的体积 V＝×S×A1O＝×a2×a＝a3.‎ 由a3＝36，得a＝6.‎ ‎18．G1，G4，G5[2015·四川卷] 一个正方体的平面展开图及该正方体的直观图的示意图如图12所示．‎ ‎(1)请将字母F，G，H标记在正方体相应的顶点处(不需说明理由)；‎ ‎(2)判断平面BEG与平面ACH的位置关系，并证明你的结论；‎ ‎(3)证明：直线DF⊥平面BEG.‎ 图12‎ ‎18．解：(1)点F，G，H的位置如图所示．‎ ‎(2)平面BEG∥平面ACH.证明如下：‎ 因为ABCDEFGH为正方体，所以BC∥FG，BC＝FG，‎ 又FG∥EH，FG＝EH，所以BC∥EH，BC＝EH，‎ 于是BCHE为平行四边形，‎ 所以BE∥CH.‎ 又CH⊂平面ACH，BE⊄平面ACH，‎ 所以BE∥平面ACH.‎ 同理BG∥平面ACH.‎ 又BE∩BG＝B，‎ 所以平面BEG∥平面ACH.‎ ‎(3)证明：连接FH.‎ 因为ABCDEFGH为正方体，所以DH⊥平面EFGH.‎ 因为EG⊂平面EFGH，所以DH⊥EG，‎ 又EG⊥FH，EG∩FH＝O，‎ 所以EG⊥平面BFHD.‎ 又DF⊂平面BFHD，所以DF⊥EG.‎ 同理DF⊥BG.‎ 又EG∩BG＝G，‎ 所以DF⊥平面BEG.‎ ‎17．G4、G5、G11[2015·天津卷] 如图14，已知AA1⊥平面ABC，BB1∥AA1，AB＝AC＝3，BC＝2，AA1＝，BB1＝2，点E和F分别为BC和A‎1C中点．‎ ‎(1)求证：EF∥平面A1B1BA；‎ ‎(2)求证：平面AEA1⊥平面BCB1；‎ ‎(3)求直线A1B1与平面BCB1所成角的大小．‎ 图14‎ ‎17．解：(1)证明：如图所示，连接A1B.在△A1BC中，因为E和F分别是BC和A‎1C的中点，所以EF∥BA1.又因为EF⊄平面A1B1BA，所以EF∥平面A1B1BA.‎ ‎(2)证明：因为AB＝AC，E为BC的中点，所以AE⊥BC.因为AA1⊥平面ABC，BB1∥AA1，所以BB1⊥平面ABC，从而BB1⊥AE.又因为BC∩BB1＝B，所以AE⊥平面BCB1.又因为AE⊂平面AEA1，所以平面AEA1⊥平面BCB1.‎ ‎(3)取BB1的中点M和B‎1C的中点N，连接A‎1M，A1N，NE.因为N和E分别为B‎1C和BC的中点，所以NE∥B1B，NE＝B1B，故NE∥A‎1A，且NE＝A‎1A，所以A1N∥AE，且A1N＝AE.又因为AE⊥平面BCB1，所以A1N⊥平面BCB1，从而∠A1B1N为直线A1B1与平面BCB1所成的角．‎ 在△ABC中，可得AE＝2，所以A1N＝AE＝2.‎ 因为BM∥AA1，BM＝AA1，所以A‎1M∥AB，A‎1M＝AB, 又由AB⊥BB1，得A‎1M⊥BB1.‎ 在Rt△A1MB1中，可得A1B1＝＝4.‎ 在Rt△A1NB1中，sin∠A1B1N＝＝，因此∠A1B1N＝30°，‎ 所以直线A1B1与平面BCB1所成的角为30°.‎ ‎4．G4，G5[2015·浙江卷] 设α，β是两个不同的平面，l，m是两条不同的直线，且l⊂α，m⊂β(　　)‎ A．若l⊥β，则α⊥β B．若α⊥β，则l⊥m ‎ C．若l∥β，则α∥β D．若α∥β，则l∥m ‎4．A　[解析] 由两平面垂直的判定定理知，A正确；对于B，直线l，m相交、平行、异面都有可能，故不正确；对于C，要求α内两条相交直线都平行于β，才能推出α∥β，故不正确；对于D，l，m平行和异面都有可能，故不正确．‎ ‎18．G5，G11[2015·浙江卷] 如图14，在三棱柱ABCA1B‎1C1中，∠BAC＝90°，AB＝AC＝2，A‎1A＝4，A1在底面ABC的射影为BC的中点，D是B‎1C1的中点．‎ ‎(1)证明：A1D⊥平面A1BC；‎ ‎(2)求直线A1B和平面BB‎1C1C所成的角的正弦值．‎ 图14‎ ‎18．解：(1)证明：设E为BC的中点，连接DE.‎ 由题意得A1E⊥平面ABC，所以A1E⊥AE.‎ 因为AB＝AC，所以AE⊥BC.‎ 故AE⊥平面A1BC.‎ 由D，E分别为B‎1C1，BC的中点，‎ 得DE∥B1B且DE＝B1B，‎ 从而DE∥A‎1A且DE＝A‎1A，‎ 所以四边形AA1DE为平行四边形．‎ 于是A1D∥AE.‎ 又因为AE⊥平面A1BC，所以A1D⊥平面A1BC.‎ ‎(2)作A‎1F⊥DE，垂足为F，连接BF.‎ 因为A1E⊥平面ABC，所以BC⊥A1E.‎ 因为BC⊥AE，所以BC⊥平面AA1DE.‎ 所以BC⊥A‎1F，所以A‎1F⊥平面BB‎1C1C.‎ 所以∠A1BF为直线A1B和平面BB‎1C1C所成的角．‎ 由AB＝AC＝2，∠CAB＝90°，得EA＝EB＝.‎ 由A1E⊥平面ABC，得A‎1A＝A1B＝4，A1E＝.‎ 由DE＝BB1＝4，DA1＝EA＝，∠DA1E＝90°，得A‎1F＝.‎ 所以sin∠A1BF＝＝.‎ ‎20．G5、G7[2015·重庆卷] 如图14，三棱锥P ABC中，平面PAC⊥平面ABC，∠ABC＝，点D，E在线段AC上，且AD＝DE＝EC＝2，PD＝PC＝4，点F在线段AB上，且 EF∥BC.‎ ‎(1)证明：AB⊥平面PFE；‎ ‎(2)若四棱锥P DFBC的体积为7，求线段BC的长．‎ 图14‎ ‎20．解：(1)证明：由DE＝EC，PD＝PC知，E为等腰三角形PDC中DC边的中点，故PE⊥AC.‎ 又平面PAC⊥平面ABC，平面PAC∩平面ABC＝AC，PE⊂平面PAC，PE⊥AC，所以PE⊥平面ABC，从而PE⊥AB.‎ 因为∠ABC＝，EF∥BC，故AB⊥EF.‎ 从而AB与平面PFE内两条相交直线PE，EF都垂直，所以AB⊥平面PFE.‎ ‎(2)设BC＝x，则在直角三角形ABC中，‎ AB＝＝，‎ 从而S△ABC＝AB·BC＝x.‎ 由EF∥BC知，＝＝，△AFE∽△ABC，故＝2＝，即S△AFE＝S△ABC.‎ 由AD＝AE，得S△AFD＝S△AFE＝×S△ABC＝S△ABC＝x，‎ 从而四边形DFBC的面积为S四边形DFBC＝S△ABC－S△AFD＝x－x＝x.‎ 由(1)知，PE⊥平面ABC，所以PE为四棱锥P DFBC的高．‎ 在直角三角形PEC中，PE＝＝＝2.‎ 所以V四棱锥PDFBC＝·S四边形DFBC·PE＝×x·2＝7，‎ 故得x4－36x2＋243＝0，解得x2＝9或x2＝27，由于x>0，可得x＝3或x＝3.‎ 所以BC＝3或BC＝3.‎ G6 多面体与球 G7 棱柱与棱锥 ‎ ‎10．G2、G7、K3[2015·湖南卷] 某工件的三视图如图13所示，现将该工件通过切削，加工成一个体积尽可能大的正方体新工件，并使新工件的一个面落在原工件的一个面内，则原工件材料的利用率为(材料利用率＝)(　　)‎ 图13‎ A. B. C. D. ‎10．A　[解析] 由三视图知，原工件是底面半径为1，母线长为3的圆锥．‎ 设新正方体工件的棱长为x，借助轴截面，由三角形相似可得，＝，得x＝，故V正＝x3＝，又V圆锥＝π×12×＝，故利用率为＝，选A.‎ ‎14．G2，G7[2015·四川卷] 在三棱柱ABCA1B‎1C1中，∠BAC＝90°，其正视图和侧视图都是边长为1的正方形，俯视图是直角边的长为1的等腰直角三角形，设点M，N，P分别是棱AB，BC，B‎1C1的中点，则三棱锥PA1MN的体积是________．‎ ‎14.　[解析] 由题意知，三棱柱的底面是直角边长为1的等腰直角三角形，棱柱的高为1且该棱柱为直三棱柱，其底面积为，三棱锥A1PMN的底面积是××1，高为，故三棱锥PA1MN的体积为××＝.‎ ‎5．G2、G7、G8[2015·重庆卷] 某几何体的三视图如图12所示，则该几何体的体积为(　　)‎ 图12‎ A.＋2π B. C. D. ‎5．B　[解析] 由三视图知，该几何体为一个圆柱与一个半圆锥的组合体，其中圆柱的底面半径为1、高为2，半圆锥的底面半径为1、高为1，所以该几何体的体积V＝××π×12×1＋π×12×2＝.‎ ‎20．G5、G7[2015·重庆卷] 如图14，三棱锥P ABC中，平面PAC⊥平面ABC，∠ABC＝，点D，E在线段AC上，且AD＝DE＝EC＝2，PD＝PC＝4，点F在线段AB上，且EF∥BC.‎ ‎(1)证明：AB⊥平面PFE；‎ ‎(2)若四棱锥P DFBC的体积为7，求线段BC的长．‎ 图14‎ ‎20．解：(1)证明：由DE＝EC，PD＝PC知，E为等腰三角形PDC中DC边的中点，故PE⊥AC.‎ 又平面PAC⊥平面ABC，平面PAC∩平面ABC＝AC，PE⊂平面PAC，PE⊥AC，所以PE⊥平面ABC，从而PE⊥AB.‎ 因为∠ABC＝，EF∥BC，故AB⊥EF.‎ 从而AB与平面PFE内两条相交直线PE，EF都垂直，所以AB⊥平面PFE.‎ ‎(2)设BC＝x，则在直角三角形ABC中，‎ AB＝＝，‎ 从而S△ABC＝AB·BC＝x.‎ 由EF∥BC知，＝＝，△AFE∽△ABC，故＝2＝，即S△AFE＝S△ABC.‎ 由AD＝AE，得S△AFD＝S△AFE＝×S△ABC＝S△ABC＝x，‎ 从而四边形DFBC的面积为S四边形DFBC＝S△ABC－S△AFD＝x－x＝x.‎ 由(1)知，PE⊥平面ABC，所以PE为四棱锥P DFBC的高．‎ 在直角三角形PEC中，PE＝＝＝2.‎ 所以V四棱锥PDFBC＝·S四边形DFBC·PE＝×x·2＝7，‎ 故得x4－36x2＋243＝0，解得x2＝9或x2＝27，由于x>0，可得x＝3或x＝3.‎ 所以BC＝3或BC＝3.‎ ‎9．G7[2015·江苏卷] 现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱各一个．若将它们重新制作成总体积与高均保持不变，但底面半径相同的新的圆锥和圆柱各一个，则新的底面半径为________．‎ ‎9.　[解析] 设新的底面半径为r，则π×52×4＋π×22×8＝πr2×4＋πr2×8 ，即πr2＝π＋32π，解得r＝.‎ G8 多面体与球 ‎5．G2、G7、G8[2015·重庆卷] 某几何体的三视图如图12所示，则该几何体的体积为(　　)‎ 图12‎ A.＋2π B. C. D. ‎5．B　[解析] 由三视图知，该几何体为一个圆柱与一个半圆锥的组合体，其中圆柱的底面半径为1、高为2，半圆锥的底面半径为1、高为1，所以该几何体的体积V＝××π×12×1＋π×12×2＝.‎ ‎10．G8[2015·全国卷Ⅱ] 已知A，B是球O的球面上两点，∠AOB＝90°，C为该球面上的动点．若三棱锥O ABC体积的最大值为36，则球O的表面积为(　　)‎ A．36π B．64π C．144π D．256π ‎10．C　[解析] 因为V三棱锥O ABC＝V三棱锥C OAB，所以三棱锥O ABC体积的最大值即三棱锥C OAB体积的最大值，所以当C到平面OAB的距离最大时，即CO⊥平面OAB时，体积最大，设球的半径为r，则V三棱锥O ABC＝V三棱锥C OAB＝r3＝36，所以r＝6，则球O的表面积S＝4πr2＝144π.‎ 图12‎ A.＋2π B. C. D. G9　空间向量及运算 G10 空间向量解决线面位置关系 G11 空间角与距离的求法 ‎17．G4、G5、G11[2015·天津卷] 如图14，已知AA1⊥平面ABC，BB1∥AA1，AB＝AC＝3，BC＝2，AA1＝，BB1＝2，点E和F分别为BC和A‎1C中点．‎ ‎(1)求证：EF∥平面A1B1BA；‎ ‎(2)求证：平面AEA1⊥平面BCB1；‎ ‎(3)求直线A1B1与平面BCB1所成角的大小．‎ 图14‎ ‎17．解：(1)证明：如图所示，连接A1B.在△A1BC中，因为E和F分别是BC和A‎1C的中点，所以EF∥BA1.又因为EF⊄平面A1B1BA，所以EF∥平面A1B1BA.‎ ‎(2)证明：因为AB＝AC，E为BC的中点，所以AE⊥BC.因为AA1⊥平面ABC，BB1∥AA1，所以BB1⊥平面ABC，从而BB1⊥AE.又因为BC∩BB1＝B，所以AE⊥平面BCB1.又因为AE⊂平面AEA1，所以平面AEA1⊥平面BCB1.‎ ‎(3)取BB1的中点M和B‎1C的中点N，连接A‎1M，A1N，NE.因为N和E分别为B‎1C和BC的中点，所以NE∥B1B，NE＝B1B，故NE∥A‎1A，且NE＝A‎1A，所以A1N∥AE，且A1N＝AE.又因为AE⊥平面BCB1，所以A1N⊥平面BCB1，从而∠A1B1N为直线A1B1与平面BCB1所成的角．‎ 在△ABC中，可得AE＝2，所以A1N＝AE＝2.‎ 因为BM∥AA1，BM＝AA1，所以A‎1M∥AB，A‎1M＝AB, 又由AB⊥BB1，得A‎1M⊥BB1.‎ 在Rt△A1MB1中，可得A1B1＝＝4.‎ 在Rt△A1NB1中，sin∠A1B1N＝＝，因此∠A1B1N＝30°，‎ 所以直线A1B1与平面BCB1所成的角为30°.‎ ‎18．G5，G11[2015·浙江卷] 如图14，在三棱柱ABCA1B‎1C1中，∠BAC＝90°，AB＝AC＝2，A‎1A＝4，A1在底面ABC的射影为BC的中点，D是B‎1C1的中点．‎ ‎(1)证明：A1D⊥平面A1BC；‎ ‎(2)求直线A1B和平面BB‎1C1C所成的角的正弦值．‎ 图14‎ ‎18．解：(1)证明：设E为BC的中点，连接DE.‎ 由题意得A1E⊥平面ABC，所以A1E⊥AE.‎ 因为AB＝AC，所以AE⊥BC.‎ 故AE⊥平面A1BC.‎ 由D，E分别为B‎1C1，BC的中点，‎ 得DE∥B1B且DE＝B1B，‎ 从而DE∥A‎1A且DE＝A‎1A，‎ 所以四边形AA1DE为平行四边形．‎ 于是A1D∥AE.‎ 又因为AE⊥平面A1BC，所以A1D⊥平面A1BC.‎ ‎(2)作A‎1F⊥DE，垂足为F，连接BF.‎ 因为A1E⊥平面ABC，所以BC⊥A1E.‎ 因为BC⊥AE，所以BC⊥平面AA1DE.‎ 所以BC⊥A‎1F，所以A‎1F⊥平面BB‎1C1C.‎ 所以∠A1BF为直线A1B和平面BB‎1C1C所成的角．‎ 由AB＝AC＝2，∠CAB＝90°，得EA＝EB＝.‎ 由A1E⊥平面ABC，得A‎1A＝A1B＝4，A1E＝.‎ 由DE＝BB1＝4，DA1＝EA＝，∠DA1E＝90°，得A‎1F＝.‎ 所以sin∠A1BF＝＝.‎ ‎18．G4，G5，G11[2015·广东卷] 如图13，三角形PDC所在的平面与长方形ABCD所在的平面垂直，PD＝PC＝4，AB＝6，BC＝3.‎ ‎(1)证明：BC∥平面PDA；‎ ‎(2)证明：BC⊥PD；‎ ‎(3)求点C到平面PDA的距离．‎ 图13‎ 图14‎ ‎22．G11、G12[2015·江苏卷] 如图16，在四棱锥P ABCD中，已知PA⊥平面ABCD，且四边形ABCD为直角梯形，∠ABC＝∠BAD＝，PA＝AD＝2，AB＝BC＝1.‎ ‎(1)求平面PAB与平面PCD所成二面角的余弦值；‎ ‎(2)点Q是线段BP上的动点，当直线CQ与DP所成的角最小时，求线段BQ的长．‎ 图16‎ ‎22．解：以{，，}为正交基底建立如图所示的空间直角坐标系A xyz，则各点的坐标为B(1，0，0)，C(1，1，0)，D(0，2，0)，P(0，0，2)．‎ ‎(1)因为AD⊥平面PAB，所以是平面PAB的一个法向量，＝(0，2，0)．‎ 因为＝(1，1，－2)，＝(0，2，－2)，‎ 设平面PCD的一个法向量为m＝(x，y，z)，‎ 所以m·＝0，m·＝0，‎ 即令y＝1，解得z＝1，x＝1，‎ 所以m＝(1，1，1)是平面PCD的一个法向量．‎ 从而cos〈，m〉＝＝，‎ 所以平面PAB与平面PCD所成二面角的余弦值为.‎ ‎(2)由＝(－1，0，2)，可设＝λ＝(－λ，0，2λ)(0≤λ≤1)，‎ 又＝(0，－1，0)，所以＝＋＝(－λ，－1，2λ)，又＝(0，－2，2)，‎ 从而cos〈，〉＝＝ .‎ 设1＋2λ＝t，t∈[1，3]，则cos2〈，〉＝＝≤，‎ 当且仅当t＝，即λ＝时，|cos〈，〉|取得最大值为.‎ 因为y＝cos x在上是减函数，所以此时直线CQ与DP所成角取得最小值．‎ 又因为BP＝＝，所以BQ＝BP＝.‎ ‎ G12 单元综合 ‎6．G12[2015·全国卷Ⅰ] 《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺．问：积及为米几何？”其意思为：“在屋内墙角处堆放米(如图11，米堆为一个圆锥的四分之一)，米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有(　　)‎ 图11‎ A．14斛 B．22斛 C．36斛 D．66斛 ‎6．B　[解析] 米堆的体积即为四分之一的圆锥的体积，设圆锥底面半径为r，则×2πr＝8，得r＝，所以米堆的体积为×πr2×5≈(立方尺)，÷1.62≈22(斛)．‎ ‎22．G11、G12[2015·江苏卷] 如图16，在四棱锥P ABCD中，已知PA⊥平面ABCD ‎，且四边形ABCD为直角梯形，∠ABC＝∠BAD＝，PA＝AD＝2，AB＝BC＝1.‎ ‎(1)求平面PAB与平面PCD所成二面角的余弦值；‎ ‎(2)点Q是线段BP上的动点，当直线CQ与DP所成的角最小时，求线段BQ的长．‎ 图16‎ ‎22．解：以{，，}为正交基底建立如图所示的空间直角坐标系A xyz，则各点的坐标为B(1，0，0)，C(1，1，0)，D(0，2，0)，P(0，0，2)．‎ ‎(1)因为AD⊥平面PAB，所以是平面PAB的一个法向量，＝(0，2，0)．‎ 因为＝(1，1，－2)，＝(0，2，－2)，‎ 设平面PCD的一个法向量为m＝(x，y，z)，‎ 所以m·＝0，m·＝0，‎ 即令y＝1，解得z＝1，x＝1，‎ 所以m＝(1，1，1)是平面PCD的一个法向量．‎ 从而cos〈，m〉＝＝，‎ 所以平面PAB与平面PCD所成二面角的余弦值为.‎ ‎(2)由＝(－1，0，2)，可设＝λ＝(－λ，0，2λ)(0≤λ≤1)，‎ 又＝(0，－1，0)，所以＝＋＝(－λ，－1，2λ)，又＝(0，－2，2)，‎ 从而cos〈，〉＝＝ .‎ 设1＋2λ＝t，t∈[1，3]，则cos2〈，〉＝＝≤，‎ 当且仅当t＝，即λ＝时，|cos〈，〉|取得最大值为.‎ 因为y＝cos x在上是减函数，所以此时直线CQ与DP所成角取得最小值．‎ 又因为BP＝＝，所以BQ＝BP＝.‎ ‎19．G12[2015·安徽卷] 如图15，三棱锥PABC中，PA⊥平面ABC，PA＝1，AB＝1，AC＝2，∠BAC＝60°.‎ ‎(1)求三棱锥PABC的体积；‎ ‎(2)证明：在线段PC上存在点M，使得AC⊥BM，并求的值．‎ 图15‎ ‎19．解：(1)由题设AB＝1，AC＝2，∠BAC＝60°，‎ 可得S△ABC＝·AB·AC·sin 60°＝.‎ 由PA⊥平面ABC，可知PA是三棱锥PABC的高，又PA＝1，所以三棱锥PABC的体积V＝·S△ABC·PA＝.‎ ‎(2)证明：在平面ABC内，过点B作BN⊥AC，垂足为N.在平面PAC内，过点N作MN∥PA，交PC于点M，连接BM.由PA⊥平面ABC知PA⊥AC，又MN∥PA，所以MN⊥AC.又BN⊥AC，BN∩MN＝N，BN⊂平面MBN，MN⊂平面MBN，所以AC⊥平面MBN.又BM⊂平面MBN，所以AC⊥BM.‎ 在Rt△BAN中，AN＝AB·cos∠BAC＝，从而NC＝AC－AN＝.由MN∥PA，得＝＝.‎ ‎20．G5、G12[2015·湖北卷] 《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．‎ 在如图14所示的阳马P ABCD中，侧棱PD⊥底面ABCD，且PD＝CD，点E是PC 的中点，连接DE，BD，BE.‎ ‎(1)证明：DE⊥平面PBC.试判断四面体EBCD是否为鳖臑，若是，写出其每个面的直角(只需写出结论)；若不是，请说明理由．‎ ‎(2)记阳马P ABCD的体积为V1，四面体EBCD的体积为V2，求的值．‎ 图14‎ ‎20．解：(1)证明：因为PD⊥底面ABCD，所以PD⊥BC.‎ 由底面ABCD为长方形，有BC⊥CD，而PD∩CD＝D，‎ 所以BC⊥平面PCD.又DE⊂平面PCD，所以BC⊥DE.‎ 又因为PD＝CD，点E是PC的中点，所以DE⊥PC.‎ 而PC∩BC＝C，所以DE⊥平面PBC.‎ 由BC⊥平面PCD，DE⊥平面PBC，可知四面体EBCD的四个面都是直角三角形，‎ 即四面体EBCD是一个鳖臑，其四个面的直角分别是∠BCD，∠BCE，∠DEC，∠DEB.‎ ‎(2)由已知，PD是阳马P ABCD的高，所以V1＝S长方形ABCD·PD＝BC·CD·PD；‎ 由(1)知，DE是鳖臑D BCE的高，BC⊥CE，‎ 所以V2＝S△BCE·DE＝BC·CE·DE.‎ 在Rt△PDC中，因为PD＝CD，点E是PC的中点，所以DE＝CE＝CD.‎ 于是＝＝＝4.‎ ‎20．G5、G12[2015·福建卷] 如图15，AB是圆O的直径，点C是圆O上异于A，B的点，PO垂直于圆O所在的平面，且PO＝OB＝1.‎ ‎(1)若D为线段AC的中点，求证：AC⊥平面PDO；‎ ‎(2)求三棱锥PABC体积的最大值；‎ ‎(3)若BC＝，点E在线段PB上，求CE＋OE的最小值．‎ 图15‎ ‎20．解：方法一：(1)证明：在△AOC中，因为OA＝OC，D为AC的中点，‎ 所以AC⊥DO.‎ 又PO垂直于圆O所在的平面，‎ 所以PO⊥AC.‎ 因为DO∩PO＝O，DO⊂平面PDO，PO⊂平面PDO，‎ 所以AC⊥平面PDO.‎ ‎(2)因为点C在圆O上，‎ 所以当CO⊥AB时，C到AB的距离最大，且最大值为1.‎ 又AB＝2，所以△ABC面积的最大值为 ×2×1＝1.‎ 又因为三棱锥PABC的高PO＝1，‎ 故三棱锥PABC体积的最大值为×1×1＝.‎ ‎(3)在△POB中，PO＝OB＝1，∠POB＝90°，‎ 所以PB＝＝.‎ 同理PC＝，所以PB＝PC＝BC.‎ 在三棱锥PABC中，将侧面BCP绕PB旋转至平面BC′P, 使之与平面ABP共面，如图所示．‎ 当O，E，C′共线时，CE＋OE取得最小值．‎ 又因为OP＝OB，C′P＝C′B，‎ 所以OC′垂直平分PB，‎ 即E为PB中点．‎ 从而OC′＝OE＋EC′＝＋＝，‎ 亦即CE＋OE的最小值为.‎ 方法二：(1)(2)同方法一．‎ ‎(3)在△POB中，PO＝OB＝1，∠POB＝90°，‎ 所以∠OPB＝45°，PB＝＝.‎ 同理PC＝.‎ 所以PB＝PC＝BC，所以∠CPB＝60°.‎ 在三棱锥PABC中，将侧面BCP绕PB旋转至平面BC′P，使之与平面ABP共面，如图所示．‎ 当O，E，C′共线时，CE＋OE取得最小值．‎ 所以在△OC′P中，由余弦定理得，‎ OC′2＝1＋2－2×1××cos(45°＋60°)＝1＋2－2 ××－×＝2＋.‎ 从而OC′＝＝.‎ 所以CE＋OE的最小值为＋.‎ ‎9．[2015·浙江五校联考] 如图K341所示，在正四棱锥S ABCD中，E，M，N分别是BC，CD，SC的中点，动点P在线段MN上运动，有四个结论：①EP⊥AC；②EP∥BD；③EP∥平面SBD；④EP⊥平面SAC.其中恒成立的为(　　)‎ 图K341‎ A．①③‎ B．③④‎ C．①②‎ D．②③④‎ ‎9．A　[解析] 连接AC，BD交于点O，连接SO，由四棱锥S ABCD为正四棱锥，可得SO⊥底面ABCD，AC⊥BD，∴SO⊥AC.∵SO∩BD＝O，∴AC⊥平面SBD.∵E，M，N分别是BC，CD，SC的中点，∴EM∥BD，MN∥SD.又EM∩MN＝M，∴平面EMN∥平面SBD，∴AC⊥平面EMN，∴AC⊥EP，故①正确．由题知EP与BD是异面直线，所以不可能有EP∥BD，故②不正确．由①可知平面EMN∥平面SBD，∴EP∥平面SBD，故③正确．由①同理可得EM⊥平面SAC，因此当P与M不重合时，EP与平面SAC不垂直，故④不正确．故选A.‎ ‎3.[2015·佛山第一中学模拟] 如图K363所示，在三棱锥P ABC中，PA⊥底面ABC，∠BCA＝90°，AP＝AC，点D，E分别在棱PB，PC上，且BC∥平面ADE.‎ ‎(1)求证：DE⊥平面PAC；‎ ‎(2)若PC⊥AD，且三棱锥P ABC的体积为8，求多面体ABCED的体积．‎ 图K363‎ ‎3．解：(1)证明：∵BC∥平面ADE，BC⊂平面PBC，平面PBC∩平面ADE＝DE，∴BC∥DE.‎ ‎∵PA⊥底面ABC，BC⊂底面ABC，‎ ‎∴PA⊥BC.∵∠BCA＝90°，∴AC⊥BC.‎ 又PA∩AC＝A，∴BC⊥平面PAC，∴DE⊥平面PAC.‎ ‎(2)由(1)知，DE⊥平面PAC，‎ ‎∵PC⊂平面PAC，∴DE⊥PC.‎ 又PC⊥AD，AD∩DE＝D，∴PC⊥平面ADE，∴AE⊥PC.‎ 又AP＝AC，∴E是PC的中点．由(1)知BC∥DE，∴DE是△PBC的中位线，‎ ‎∴＝＝，V三棱锥P ADE＝V三棱锥P ABC＝×8＝2，‎ ‎∴V多面体ABCED＝V三棱锥P ABC － V三棱锥P ADE＝8－2＝6.‎ ‎5．[2015·河北衡水中学调研] 已知三棱锥P ABC的所有棱长都相等，现沿PA，PB，PC三条侧棱剪开，将其表面展开成一个平面图形，若这个平面图形外接圆的半径为2 ，则三棱锥P ABC的内切球的体积为________．‎ ‎5.　[解析] 三棱锥P ABC展开后为一等边三角形，设边长为a，则4 ＝，∴a＝6 ，∴三棱锥P ABC的棱长为3 ，∴三棱锥P ABC的高为2 .设内切球的半径为r，则有4××r×S△ABC＝S△ABC×2 ，∴r＝，∴三棱锥P ABC的内切球的体积为πr3＝.‎ ‎3.[2015·石家庄外国语学校模拟] 如图K353所示，四棱柱ABCD A1B‎1C1D1的底面ABCD是正方形，O为底面的中心，A1O⊥平面ABCD，AB＝AA1＝.‎ ‎(1)证明：平面A1BD∥平面CD1B1；‎ ‎(2)求三棱柱ABD A1B1D1的体积．‎ 图K353‎ ‎3．解：(1)证明：设线段B1D1的中点为O1，连接A1O1，O‎1C，在四棱柱ABCD A1B‎1C1D1中，易知BD∥B1D1，A1O1∥OC且A1O1＝OC，所以四边形A1O1CO为平行四边形，所以A1O∥O‎1C.‎ 又A1O ∩ BD＝O，O‎1C ∩ B1D1＝O1，所以平面A1BD∥平面CD1B1.‎ ‎(2)因为A1O⊥平面ABCD，所以A1O是三棱柱ABD A1B1D1的高．‎ 在正方形ABCD中，AO＝1，所以在直角三角形A1OA中，A1O＝1，‎ 所以三棱柱ABD A1B1D1的体积V＝S△ABD·A1O＝×()2×1＝1.‎ ‎6．[2015·河北衡水中学调研] 如图K328所示，多面体MN ABCD的底面ABCD为矩形，其正视图和侧视图如图K329所示，其中正视图为等腰梯形，侧视图为等腰三角形，则AM的长为(　　)‎ 图K328‎ ‎　　图K329‎ A. B. C. D．2 ‎6．C　[解析] 如图所示，‎ E，F分别为AD，BC的中点，MO⊥面ABCD，则四边形MNFE为等腰梯形．由正视图为等腰梯形，可知MN＝2，AB＝4.‎ 由侧视图为等腰三角形，可知AD＝2，MO＝2，∴ME＝＝.又在△AME中，AE＝1，∴AM＝＝.‎