自考专题 线性代数(经管类)考点逐个击破 22页

线性代数（经管类）考点逐个击破 第一章 行列式 （一）行列式的定义 行列式是指一个由若干个数排列成同样的行数与列数后所得到的一个式子，它实质上 表示把这些数按一定的规则进行运算，其结果为一个确定的数. 1．二阶行列式 由 4 个数 )2,1,( jiaij 得到下列式子： 11 12 21 22 a a a a 称为一个二阶行列式，其运算规 则为 21122211 2221 1211 aaaaaa aa  2．三阶行列式 由 9 个数 )3,2,1,( jiaij 得到下列式子： 333231 232221 131211 aaa aaa aaa 称为一个三阶行列式，它如何进行运算呢？教材上有类似于二阶行列式的所谓对角线 法，我们采用递归法，为此先要定义行列式中元素的余子式及代数余子式的概念. 3．余子式及代数余子式 设有三阶行列式 333231 232221 131211 3 aaa aaa aaa D  对任何一个元素 ija ，我们划去它所在的第 i 行及第 j 列，剩下的元素按原先次序组成 一个二阶行列式，称它为元素 ija 的余子式，记成 ijM 例如 3332 2322 11 aa aaM  ， 3332 1312 21 aa aaM  ， 2322 1312 31 aa aaM  再记 ij ji ij MA  )1( ，称 ijA 为元素 ija 的代数余子式. 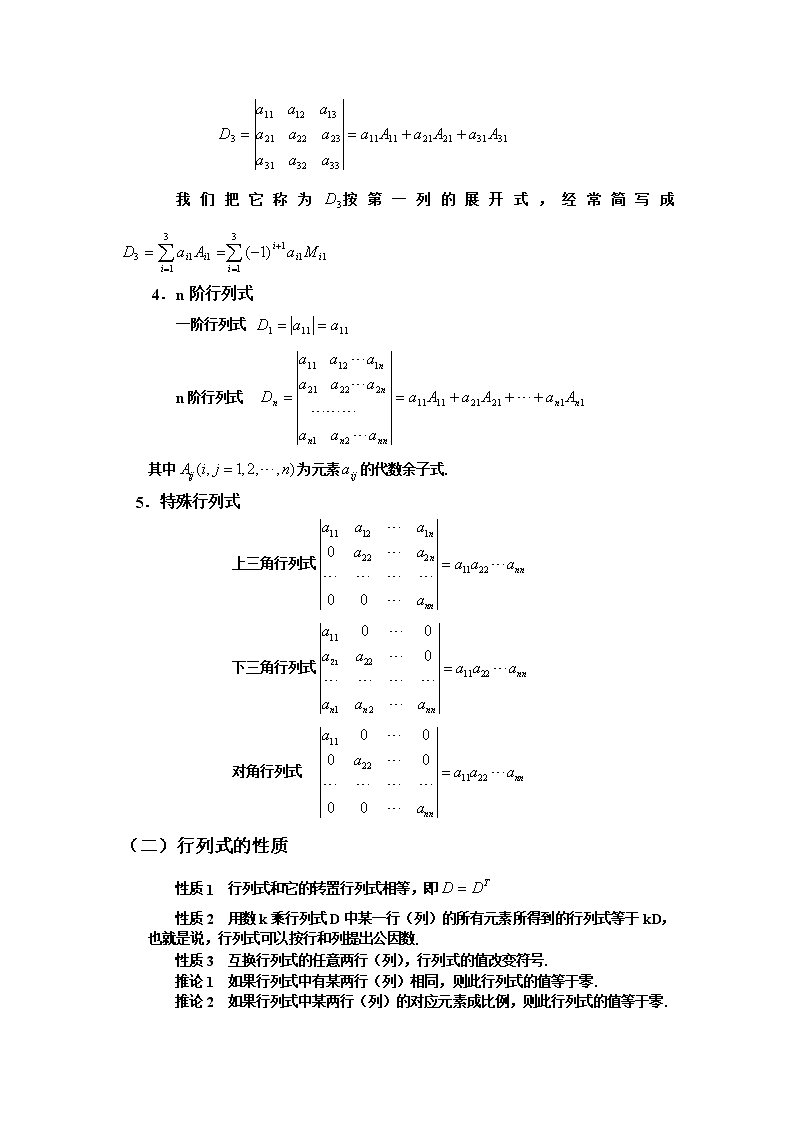例如 1111 MA  ， 2121 MA  ， 3131 MA  那么 ，三阶行列式 3D 定义为 我 们 把 它 称 为 3D 按 第 一 列 的 展 开 式 ， 经 常 简 写 成      3 1 11 1 3 1 113 )1( i ii i i ii MaAaD 4．n 阶行列式 一阶行列式 11111 aaD  n 阶行列式 1121211111 21 22221 11211 nn nnnn n n n AaAaAa aaa aaa aaa D       其中 ( , 1,2, , )ijA i j n  为元素 ija 的代数余子式. 5．特殊行列式 上三角行列式 11 12 1 22 2 11 22 0 0 0 n n nn nn a a a a a a a a a         下三角行列式 11 22 11 22 1 2 0 0 0 nn n n nn a a a a a a a a a         21 对角行列式 11 22 11 22 0 0 0 0 0 0 nn nn a a a a a a         （二）行列式的性质 性质 1 行列式和它的转置行列式相等，即 TDD  性质 2 用数 k 乘行列式 D 中某一行（列）的所有元素所得到的行列式等于 kD， 也就是说，行列式可以按行和列提出公因数. 性质 3 互换行列式的任意两行（列），行列式的值改变符号. 推论 1 如果行列式中有某两行（列）相同，则此行列式的值等于零. 推论 2 如果行列式中某两行（列）的对应元素成比例，则此行列式的值等于零. 313121211111 333231 232221 131211 3 AaAaAa aaa aaa aaa D  性质 4 行列式可以按行（列）拆开. 性质 5 把行列式 D 的某一行（列）的所有元素都乘以同一个数以后加到另一行 （列）的对应元素上去，所得的行列式仍为 D. 定理 1（行列式展开定理） n 阶行列式 nijaD  等于它的任意一行（列）的各元素与其对应的代数余子式的 乘积的和，即 ),,2,1(2211 niAaAaAaD ininiiii   或 ),,2,1(2211 njAaAaAaD njnjjjjj   前一式称为 D 按第 i 行的展开式，后一式称为 D 按第 j 列的展开式. 本定理说明，行列式可以按其任意一行或按其任意一列展开来求出它的值. 定理 2 n 阶行列式 nijaD  的任意一行（列）各元素与另一行（列）对应元素的代 数余子式的乘积之和等于零.即 )(02211 kiAaAaAa kninkiki   或 )(02211 sjAaAaAa nsnjsjsj   （三）行列式的计算 行列式的计算主要采用以下两种基本方法： （1）利用行列式性质，把原行列式化为上三角（或下三角）行列式再求值，此时 要注意的是，在互换两行或两列时，必须在新的行列式的前面乘上（－1），在按行或按列 提取公因子 k 时，必须在新的行列式前面乘上 k. （2）把原行列式按选定的某一行或某一列展开，把行列式的阶数降低，再求出它 的值，通常是利用性质在某一行或某一列中产生很多个“0”元素，再按这一行或这一列展 开： 例 1 计算行列式 5207 2325 1213 1412 4 D 解：观察到第二列第四行的元素为 0，而且第二列第一行的元素是 112 a ，利用这个 元素可以把这一列其它两个非零元素化为 0，然后按第二列展开. 4 2 1 4 1 2 1 4 1 5 6 23 1 2 1 2 1 1 5 0 6 2 1 5 05 2 3 2 1 0 5 03 ( 2) 1 7 2 50 2 5 7 0 2 5 5 31 2 31 22 5 1 1 0 0 8137 57 37 5 D           行 行 按第二列展开 行 行 7 　　列 列 按第二行展开 例 2 计算行列式 abbb babb bbab bbba D 4 解：方法 1 这个行列式的元素含有文字，在计算它的值时，切忌用文字作字母，因为 文字可能取 0 值.要注意观察其特点，这个行列式的特点是它的每一行元素之和均为 ba 3 （我们把它称为行和相同行列式），我们可以先把后三列都加到第一列上去，提 出第一列的公因子 ba 3 ，再将后三行都减去第一行： 3 1 3 1( 3 )3 1 3 1 1 0 0 0( 3 ) 0 0 0 0 0 0 a b b b a b b b b b b b b a b b a b a b b a b ba bb b a b a b b a b b a b b b b a a b b b a b b a b b b a ba b a b a b          　　　　　 3))(3( baba  方法 2 观察到这个行列式每一行元素中有多个 b，我们采用“加边法”来计算，即是 构造一个与 4D 有相同值的五阶行列式： 1 1 2 3 4 5 4 1 1 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 b b b b b b b ba b b b a b b b a bb a b bD b a b b a bb b a b b b a b a bb b b a b b b a a b               行（ ） ，，，行 这样得到一个“箭形”行列式，如果 ba  ，则原行列式的值为零，故不妨假设 ba  ， 即 0 ba ，把后四列的 ba  1 倍加到第一列上，可以把第一列的（－1）化为零. 4 41 0 0 0 0 40 0 0 0 1 ( ) ( 3 )( ) 0 0 0 0 0 0 0 0 b b b b ba b a b ba b a b a b a ba ba b a b                 例 3 三阶范德蒙德行列式 ))()(( 111 231312 2 3 2 2 2 1 3213 xxxxxx xxx xxxV  （四）克拉默法则 定理 1（克拉默法则）设含有 n 个方程的 n 元线性方程组为 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 , , n n n n n n nn n n a x a x a x b a x a x a x b a x a x a x b                    如果其系数行列式 0 nijaD ，则方程组必有唯一解： njD Dx j j ,,2,1,  其中 jD 是把 D 中第 j 列换成常数项 nbbb ,,, 21  后得到的行列式. 把这个法则应用于齐次线性方程组，则有 定理 2 设有含 n 个方程的 n 元齐次线性方程组 11 1 12 2 1 21 1 22 2 2 1 1 2 2 0, 0, 0 n n n n n n nn n a x a x a x a x a x a x a x a x a x                    如果其系数行列式 0D ，则该方程组只有零解： 021  nxxx  换句话说，若齐次线性方程组有非零解，则必有 0D ，在教材第二章中，将要证明， n 个方程的 n 元齐次线性方程组有非零解的充分必要条件是系数行列式等于零. 第二章 矩阵 （一）矩阵的定义 1．矩阵的概念 由 nm 个数 ),,2,1;,,2,1( njmiaij   排成的一个 m 行 n 列的数表              mnmm n n aaa aaa aaa A     21 22221 11211 称为一个 m 行 n 列矩阵或 nm 矩阵 当 nm  时，称   nnijaA  为 n 阶矩阵或 n 阶方阵 元素全为零的矩阵称为零矩阵，用 nmO  或 O 表示 2．3 个常用的特殊方阵： ①n 阶对角矩阵是指形如              nna a a A     00 00 00 22 11 的矩阵 ②n 阶单位方阵是指形如              100 010 001     nE 的矩阵 ③n 阶三角矩阵是指形如                         nnnnnn n n aaa aa a a aa aaa         21 2221 11 222 11211 0 00 , 00 0 的矩阵 3．矩阵与行列式的差异 矩阵仅是一个数表，而 n 阶行列式的最后结果为一个数，因而矩阵与行列式是两 个完全不同的概念，只有一阶方阵是一个数，而且行列式记号“ * ”与矩阵记号“ * ” 也不同，不能用错. （二）矩阵的运算 1．矩阵的同型与相等 设有矩阵 nmijaA  )( ，  kijbB )( ，若 km  ， n ，则说 A 与 B 是同型矩 阵.若 A 与 B 同型,且对应元素相等，即 ijij ba  ，则称矩阵 A 与 B 相等，记为 BA  因而只有当两个矩阵从型号到元素全一样的矩阵，才能说相等. 2．矩阵的加、减法 设 nmijaA  )( ， nmijbB  )( 是两个同型矩阵则规定 nmijij baBA  )( nmijij baBA  )( 注意：只有 A 与 B 为同型矩阵，它们才可以相加或相减. 由于矩阵的相加体现为元素的相加，因而与普通数的加法运算有相同的运算律. 3．数乘运算 设 nmijaA  )( ，k 为任一个数，则规定 nmijkakA  )( 故数 k 与矩阵 A 的乘积就是 A 中所有元素都乘以 k，要注意数 k 与行列式 D 的乘 积，只是用 k 乘行列式中某一行或某一列，这两种数乘截然不同. 矩阵的数乘运算具有普通数的乘法所具有的运算律. 4．乘法运算 设 kmijaA  )( ， nkijbB  )( ，则规定 nmijcAB  )( 其中 kjikjijiij bababac  2211 ),,2,1;,,2,1( njmi   由此定义可知，只有当左矩阵 A 的列数与右矩阵 B 的行数相等时，AB 才有意义， 而且矩阵 AB 的行数为 A 的行数，AB 的列数为 B 的列数，而矩阵 AB 中的元素是由左矩阵 A 中某一行元素与右矩阵 B 中某一列元素对应相乘再相加而得到. 故矩阵乘法与普通数的乘法有所不同，一般地： ①不满足交换律，即 BAAB  ②在 0AB 时，不能推出 0A 或 0B ，因而也不满足消去律. 特别，若矩阵 A 与 B 满足 BAAB  ，则称 A 与 B 可交换，此时 A 与 B 必为同阶 方阵. 矩阵乘法满足结合律，分配律及与数乘的结合律. 5．方阵的乘幂与多项式方阵 设 A 为 n 阶方阵，则规定 mA AA A  m个 特别 EA 0 又若 1 1 1 0( ) m m m mf x a x a x a x a      ，则规定 1 1 1 0( ) m m m mf A a A a A a A a E      称 )(Af 为 A 的方阵多项式，它也是一个 n 阶方阵 6．矩阵的转置 设 A 为一个 nm 矩阵，把 A 中行与列互换，得到一个 mn 矩阵，称为 A 的转 置矩阵，记为 TA ，转置运算满足以下运算律： AA T  )( ， TTT BABA  )( ， TT kAkA )( ， TTT ABAB )( 由转置运算给出对称矩阵，反对称矩阵的定义 设 A 为一个 n 阶方阵，若 A 满足 AAT  ，则称 A 为对称矩阵，若 A 满足 AAT  ， 则称 A 为反对称矩阵. 7．方阵的行列式 矩阵与行列式是两个完全不同的概念，但对于 n 阶方阵，有方阵的行列式的概念. 设 )( ijaA  为一个 n 阶方阵，则由 A 中元素构成一个 n 阶行列式 nija ，称为方阵 A 的行列式，记为 A 方阵的行列式具有下列性质：设 A，B 为 n 阶方阵，k 为数，则 ① AAT  ； ② AkkA n ③ BAAB  （三）方阵的逆矩阵 1．可逆矩阵的概念与性质 设 A 为一个 n 阶方阵，若存在另一个 n 阶方阵 B，使满足 EBAAB  ，则把 B 称为 A 的逆矩阵，且说 A 为一个可逆矩阵，意指 A 是一个可以存在逆矩阵的矩阵，把 A 的 逆矩阵 B 记为 1A ，从而 A 与 1A 首先必可交换，且乘积为单位方阵 E. 逆矩阵具有以下性质：设 A，B 为同阶可逆矩阵， 0k 为常数，则 ① 1A 是可逆矩阵，且 AA  11 )( ； ②AB 是可逆矩阵，且 111)(   ABAB ； ③kA 是可逆矩阵，且 11 1)(   AkkA ④ TA 是可逆矩阵，且 TT AA )()( 11   ⑤可逆矩阵可从矩阵等式的同侧消去，即 设 P 为可逆矩阵，则 BAPBPA  BABPAP  2．伴随矩阵 设 )( ijaA  为一个 n 阶方阵， ijA 为 A 的行列式 nijaA  中元素 ija 的代数余子 式，则矩阵             nnnn n n AAA AAA AAA     21 22212 12111 称为 A 的伴随矩阵，记为 *A （务必注意 *A 中元素排列 的特点） 伴随矩阵必满足 EAAAAA  ** 1*  nAA （n 为 A 的阶数） 3．n 阶阵可逆的条件与逆矩阵的求法 定理：n 阶方阵 A 可逆  0A ，且 *1 1 AAA  推论：设 A，B 均为 n 阶方阵，且满足 EAB  ，则 A，B 都可逆，且 BA 1 ， AB 1 例 1 设       dc baA （1）求 A 的伴随矩阵 *A （2）a，b，c，d 满足什么条件时，A 可逆？此时求 1A 解：（1）对二阶方阵 A，求 *A 的口诀为“主交换，次变号”即         ac bdA* （2）由 bcaddc baA  ，故当 0 bcad 时，即 0A ，A 为可逆 矩阵 此时          ac bd bcadAAA 11 *1 （四）分块矩阵 1． 分块矩阵的概念与运算 对于行数和列数较高的矩阵，为了表示方便和运算简洁，常用一些贯穿于矩阵的横 线和纵线把矩阵分割成若干小块，每个小块叫做矩阵的子块，以子块为元素的形式上的 矩阵叫做分块矩阵. 在作分块矩阵的运算时，加、减法，数乘及转置是完全类似的，特别在乘法时，要 注意到应使左矩阵 A 的列分块方式与右矩阵 B 的行分块方式一致，然后把子块当作元 素来看待，相乘时 A 的各子块分别左乘 B 的对应的子块. 2．准对角矩阵的逆矩阵 形如             rA A A  2 1 的分块矩阵称为准对角矩阵，其中 rAAA ,,, 21  均为方阵空 白处都是零块. 若 rAAA ,,, 21  都是可逆矩阵，则这个准对角矩阵也可逆，并且                               1 1 2 1 1 1 2 1 rr A A A A A A  （五）矩阵的初等变换与初等方阵 1． 初等变换 对一个矩阵 A 施行以下三种类型的变换，称为矩阵的初等行（列）变换，统称为 初等变换， （1）交换 A 的某两行（列）； （2）用一个非零数 k 乘 A 的某一行（列）； （3）把 A 中某一行（列）的 k 倍加到另一行（列）上. 注意：矩阵的初等变换与行列式计算有本质区别，行列式计算是求值过程，用等号 连接，而对矩阵施行初等变换是变换过程用“  ”连接前后矩阵. 初等变换是矩阵理论中一个常用的运算，而且最常见的是利用矩阵的初等行变换把 矩阵化成阶梯形矩阵，以至于化为行简化的阶梯形矩阵. 2．初等方阵 由单位方阵 E 经过一次初等变换得到的矩阵称为初等方阵. 由于初等变换有三种类型，相应的有三种类型的初等方阵，依次记为 ijP ， )(kDi 和 )(kTij ，容易证明，初等方阵都是可逆矩阵，且它们的逆矩阵还是同一类的初等方阵. 3．初等变换与初等方阵的关系 设 A 为任一个矩阵，当在 A 的左边乘一个初等方阵的乘积相当于对 A 作同类型的 初等行变换；在 A 的右边乘一个初等方阵的乘积相当于对 A 作同类型的初等列变换. 4．矩阵的等价与等价标准形 若矩阵 A 经过若干次初等变换变为 B，则称 A 与 B 等价，记为 BA  对任一个 nm 矩阵 A，必与分块矩阵       OO OEr 等价，称这个分块矩阵为 A 的等 价标准形.即对任一个 nm 矩阵 A，必存在 n 阶可逆矩阵 P 及 n 阶可逆矩阵 Q，使得       OO OEPAQ r 5．用初等行变换求可逆矩阵的逆矩阵 设 A 为任一个 n 阶可逆矩阵，构造 nn 2 矩阵（A，E） 然后 ),(),( 1 AEEA 注意：这里的初等变换必须是初等行变换. 例 2 求               421 412 311 A 的逆矩阵 解：       1 2 2 1 1 3 2 1 1 3 1 1 2 1 3 3 2 2 1 1 3 1 0 0 1 1 3 1 0 0 ( , ) 2 1 4 0 1 0 0 1 2 2 1 0 1 2 4 0 0 1 0 1 1 1 0 1 1 0 1 1 1 0 1 0 0 4 2 1 0 1 2 2 1 0 0 1 0 4 1 2 0 0 1 3 1 1 0 0 1 3 1 1 A E                                                                行 行 行 行 行 行 行 行 行 行 行 行 则               113 214 124 1A 例 3 求解矩阵方程                         21 34 11 421 412 311 X 解：令                          21 34 11 , 421 412 311 BA ，则矩阵方程为 BAX  ，这里 A 即为例 2 中 矩阵，是可逆的，在矩阵方程两边左乘 1A ，得                                     20 52 03 21 34 11 113 214 124 1BAX 也能用初等行变换法，不用求出 1A ，而直接求 BA 1 ),( 20100 52010 03001 21421 34412 11311 ),( 1BAEBA                           则             20 52 03 1BAX （六）矩阵的秩 1． 秩的定义 设 A 为 nm 矩阵，把 A 中非零子式的最高阶数称为 A 的秩，记为秩 )(A 或 )(Ar 零矩阵的秩为 0，因而  nmA ,min)(0  秩 ，对 n 阶方阵 A，若秩 nA )( ，称 A 为满秩矩阵，否则称为降秩矩阵. 2． 秩的求法 由于阶梯形矩阵的秩就是矩阵中非零行的行数，又矩阵初等变换不改变矩阵的秩. 对任一个矩阵 A，只要用初等行变换把 A 化成阶梯形矩阵 T，则秩(A)=秩(T)=T 中非零 行的行数. 3．与满秩矩阵等价的条件 n 阶方阵 A 满秩  A 可逆，即存在 B，使 EBAAB   A 非奇异，即 0A  A 的等价标准形为 E  A 可以表示为有限个初等方阵的乘积  齐次线性方程组 0AX 只有零解  对任意非零列向量 b，非齐次线性方程组 bAX  有唯一解  A 的行（列）向量组线性无关  A 的行（列）向量组为 nR 的一个基  任意 n 维行（列）向量均可以表示为 A 的行（列）向量组 的线性组合，且表示法唯一.  A 的特征值均不为零  AAT 为正定矩阵. （七）线性方程组的消元法. 对任一个线性方程组          mnmnmm nn nn bxaxaxa bxaxaxa bxaxaxa     2211 22222121 11212111 可以表示成矩阵形式 bAX  ，其中 nmijaA  )( 为系数矩阵， T mbbbb ),,,( 21  为 常数列矩阵， T nxxxX ),,,( 21  为未知元列矩阵. 从而线性方程组 bAX  与增广矩阵 ),( bAA  一一对应. 对于给定的线性方程组，可利用矩阵的初等行变换，把它的增广矩阵化成简化阶 梯形矩阵，从而得到易于求解的同解线性方程组，然后求出方程组的解. 第三章 向量空间 （一）n 维向量的定义与向量组的线性组合 1． n 维向量的定义与向量的线性运算 由 n 个数组成的一个有序数组称为一个 n 维向量，若用一行表示，称为 n 维行向 量，即 n1 矩阵，若用一列表示，称为 n 维列向量，即 1n 矩阵 与矩阵线性运算类似，有向量的线性运算及运算律. 2．向量的线性组合 设 m ,,, 21  是一组 n 维向量， mkkk ,,, 21  是一组常数，则称 mmkkk   2211 为 m ,,, 21  的一个线性组合，常数 mkkk ,,, 21  称为组合系数. 若一个向量  可以表示成 mmkkk   2211 则称  是 m ,,, 21  的线性组合，或称  可用 m ,,, 21  线性表出. 3．矩阵的行、列向量组 设 A 为一个 nm 矩阵，若把 A 按列分块，可得一个 m 维列向量组称之为 A 的 列向量组. 若把 A 按行分块，可得一个 n 维行向量组称之为 A 的行向量组. 4．线性表示的判断及表出系数的求法. 向量  能用 m ,,, 21  线性表出的充要条件是线性方程组   mmxxx 2211 有解，且每一个解就是一个组合系数. 例 1 问 T)5,1,1( 能否表示成 T)3,2,1(1  ， T)4,1,0(2  ， T)6,3,2(3  的线 性组合？ 解：设线性方程组为   332211 xxx 对方程组的增广矩阵作初等行变换：                         1100 2010 1001 5643 1312 1201 ),,,(),( 321 A 则方程组有唯一解 1,2,1 321  xxx 所以  可以唯一地表示成 321 ,,  的线性组合，且 321 2   （二）向量组的线性相关与线性无关 1． 线性相关性概念 设 m ,,, 21  是 m 个 n 维向量，如果存在 m 个不全为零的数 mkkk ,,, 21  ，使 得 02211  mmkkk   ，则称向量组 m ,,, 21  线性相关，称 mkkk ,,, 21  为 相关系数.否则，称向量 m ,,, 21  线性无关. 由定义可知， m ,,, 21  线性无关就是指向量等式 02211  mmkkk   当且仅当 021  mkkk  时成立. 特别 单个向量 线性相关  0 ； 单个向量 线性无关  0 2．求相关系数的方法 设 m ,,, 21  为 m 个 n 维列向量，则 m ,,, 21  线性相关  m 元齐次线性 方程组 02211  mmxxx   有非零解，且每一个非零解就是一个相关系数  矩阵 ),,,( 21 mA   的秩小于 m 例 2 设向量组 1 2 3(2, 1,7) , (1,4,11) , (3, 6,3)T T T       ，试讨论其线性相关性. 解：考虑方程组 0332211   xxx 其系数矩阵                       000 110 201 3117 641 312 ),,( 321 A 于是，秩 32)( A ，所以向量组线性相关，与方程组同解的方程组为      0 02 32 31 xx xx 令 13 x ，得一个非零解为 1,1,2 321  xxx 则 02 321   3．线性相关性的若干基本定理 定理 1 n 维向量组 m ,,, 21  线性相关  至少有一个向量是其余向量的线性 组合.即 m ,,, 21  线性无关  任一个向量都不能表示为其余向量的线性组合. 定理 2 如果向量组 m ,,, 21  线性无关，又 m ,,,, 21  线性相关，则  可以用 m ,,, 21  线性表出，且表示法是唯一的. 定理 3 若向量组中有部分组线性相关，则整体组也必相关，或者整体无关，部分 必无关. 定理 4 无关组的接长向量组必无关. （三）向量组的极大无关组和向量组的秩 1．向量组等价的概念 若向量组 S 可以由向量组 R 线性表出，向量组 R 也可以由向量组 S 线性表出，则 称这两个向量组等价. 2．向量组的极大无关组 设 T 为一个向量组，若存在 T 的一个部分组 S，它是线性无关的，且 T 中任一个 向量都能由 S 线性表示，则称部分向量组 S 为 T 的一个极大无关组. 显然，线性无关向量组的极大无关组就是其本身. 对于线性相关的向量组，一般地，它的极大无关组不是唯一的，但有以下性质： 定理 1 向量组 T 与它的任一个极大无关组等价，因而 T 的任意两个极大无关组 等价. 定理 2 向量组 T 的任意两个极大无关组所含向量的个数相同. 3．向量组的秩与矩阵的秩的关系 把向量组 T 的任意一个极大无关组中的所含向量的个数称为向量组 T 的秩. 把矩阵 A 的行向量组的秩，称为 A 的行秩，把 A 的列向量组的秩称为 A 的列秩. 定理：对任一个矩阵 A，A 的列秩=A 的行秩=秩（A） 此定理说明，对于给定的向量组，可以按照列构造一个矩阵 A，然后用矩阵的初 等行变换法来求出向量组的秩和极大无关组. 例 3 求出下列向量组的秩和一个极大无关组，并将其余向量用极大无关组线性表出： )3,4,4,2(),3,4,1,2(),6,6,1,1(),9,2,,2,1(),7,2,1,1( 54321   解：把所有的行向量都转置成列向量，构造一个 54 矩阵，再用初等行变换把它化成 简化阶梯形矩阵   BA TTTTT                                 10000 01100 01010 00001 33697 44622 41121 22111 ,,,, 54321  易见 B 的秩为 4，A 的秩为 4，从而秩   4,,,, 54321  ，而且 B 中主元位 于第一、二、三、五列，那么相应地 5321 ,,,  为向量组的一个极大无关组， 而且 324   （四）向量空间 1． 向量空间及其子空间的定义 定义 1 n 维实列向量全体（或实行向量全体）构成的集合称为实 n 维向量空间， 记作 nR 定义 2 设 V 是 n 维向量构成的非空集合，若 V 对于向量的线性运算封闭，则称 集合 V 是 nR 的子空间，也称为向量空间. 2． 向量空间的基与维数 设 V 为一个向量空间，它首先是一个向量组，把该向量组的任意一个极大无关组 称为向量空间 V 的一个基，把向量组的秩称为向量空间的维数. 显然，n 维向量空间 nR 的维数为 n，且 nR 中任意 n 个线性无关的向量都是 nR 的 一个基. 3． 向量在某个基下的坐标 设 r ,,, 21  是向量空间 V 的一个基，则 V 中任一个向量 都可以用 r ,,, 21  唯一地线性表出，由 r 个表出系数组成的 r 维列向量称为向量 在此基 下的坐标. 第四章 线性方程组 （一） 线性方程组关于解的结论 定理 1 设 bAX  为 n 元非齐次线性方程组，则它有解的充要条件是 )(),( ArbAr  定理 2 当 n 元非齐次线性方程组 bAX  有解时，即 rArbAr  )(),( 时，那 么 （1） bAX  有唯一解  nr  ； （2） bAX  有无穷多解  nr  . 定理 3 n 元齐次线性方程组 0AX 有非零解的充要条件是 nrAr )( 推论 1 设 A 为 n 阶方阵，则 n 元齐次线性方程组 0AX 有非零解  0A 推论 2 设 A 为 nm 矩阵，且 nm  ，则 n 元齐次线性方程组必有非零解 （二）齐次线性方程组解的性质与解空间 首先对任一个线性方程组，我们把它的任一个解用一个列向量表示，称为该方程 组的解向量，也简称为方程组的解. 考虑由齐次线性方程组 0AX 的解的全体所组成的向量集合  0  AV 显然 V 是非空的，因为 V 中有零向量，即零解，而且容易证明 V 对向量的加法运算及 数乘运算封闭，即解向量的和仍为解，解向量的倍数仍为解，于是 V 成为 n 维列向量 空间 nR 的一个子空间，我们称 V 为方程组 0AX 的解空间 （三）齐次线性方程组的基础解系与通解 把 n 元齐次线性方程组 0AX 的解空间的任一个基，称为该齐次线性方程组的一 个基础解系. 当 n 元齐次线性方程组 0AX 有非零解时，即 nrAr )( 时，就一定存在基础 解系，且基础解系中所含有线性无关解向量的个数为 rn  求基础解系与通解的方法是： 对方程组 0AX 先由消元法，求出一般解，再把一般解写成向量形式，即为 方程组的通解，从中也能求出一个基础解系. 例 1 求       0 0223 0322 4321 4321 4321 xxxx xxxx xxxx 的通解 解：对系数矩阵 A，作初等行变换化成简化阶梯形矩阵： 1 22 1 2 3 1 0 3 4 1 0 3 4 3 2 1 2 1 1 1 1 0 1 4 5 1 1 1 1 1 1 1 1 0 0 0 0 A                                        行 (-1)+2行 行 (-1)+3行 3行 (-1)+1行 1行 (-1)+2行 42)( Ar ，有非零解，取 43 , xx 为自由未知量，可得一般解为           44 33 432 431 ,54 ,43 xx xx xxx xxx 写成向量形式，令 13 kx  ， 24 kx  为任意常数，则通解为                           1 0 5 4 0 1 4 3 21 kkX 可见，                           1 0 5 4 , 0 1 4 3 21  为方程组的一个基础解系. （四）非齐次线性方程组 1． 非齐次线性方程组与它对应的齐次线性方程组（即导出组）的解之 间的关系 设 bAX  为一个 n 元非齐次线性方程组， 0AX 为它的导出组，则它们的解之 间有以下性质： 性质 1 如果 21, 是 bAX  的解，则 21   是 0AX 的解 性质 2 如果 是 bAX  的解， 是 0AX 的解，则   是 bAX  的解 由这两个性质，可以得到 bAX  的解的结构定理： 定理 设 A 是 nm 矩阵，且 rArbAr  )(),( ，则方程组 bAX  的通解为 rnrnkkkX   2211 * 其中 * 为 bAX  的任一个解（称为特解）, rn ,,, 21  为导出组 0AX 的一个基 础解系. 2．求非齐次线性方程组的通解的方法 对非齐次线性方程组 bAX  ，由消元法求出其一般解，再把一般解改写为向量形 式，就得到方程组的通解. 例 2 当参数 a，b 为何值时，线性方程组           123 2)3( 122 0 4321 432 432 4321 axxxx bxxax xxx xxxx 有唯一解？有无穷多解？无解？在有无穷多解时，求出通解. 解：对方程组的增广矩阵施行初等行变换，把它化成阶梯形矩阵：     2 3 4 2 4 1 1 1 1 1 0 1 1 1 1 0 0 1 2 2 1 0 1 2 2 1( , ) 0 1 3 2 0 0 1 0 1 3 2 1 1 0 1 2 3 1 1 0 1 1 1 0 1 2 2 1 0 0 1 0 1 0 0 0 1 0 A b a b a b a a a b a                                                    行 行 １行 -3 行 行 行 2行 -1 行 当 1a 时， 4)(),(  ArbAr ，有唯一解； 当 1,1  ba 时， 3),( bAr ， 2)( Ar ，无解； 当 1,1  ba 时， 2)(),(  ArbAr ，有无穷多解. 此时，方程组的一般解为           44 33 432 431 221 1 xx xx xxx xxx 令 2413 , kxkx  为任意常数，故一般解为向量形式，得方程组通解为                                        1 0 2 1 0 1 2 1 0 0 1 1 21 kkX