浙江省名校协作体2020届高三下学期3月第二次联考数学试题 Word版含解析 29页

www.ks5u.com 高三年级数学学科线上测试 考生须知：‎ ‎1.本卷满分150分，考试时间120分钟；‎ ‎2.答题前，在答题卷指定区域填写学校、班级、姓名、试场号、座位号及准考证号.‎ ‎3.所有答案必须写在答题卷上，写在试卷上无效；‎ ‎4.考试结束后，只需上交答题卷.‎ 一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.若全集U={0，1，2，3，4，5，6，7}，集合A={3，4，5，6}，集合B={1，3，4}，则集合（ ）‎ A. {0，1，2，5，6，7} B. {1} C. {0，2，7} D. {5，6}‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 利用集合补集运算方法分别求出，，再由集合的并集运算方法求出.‎ ‎【详解】因为全集U={0，1，2，3，4，5，6，7}，集合A={3，4，5，6}，集合B={1，3，4}，则集合，，所以{0，2，7}‎ 故选择：C ‎【点睛】本题考查集合的并集与补集运算，属于基础题.‎ ‎2.已知双曲线=1(a>0，b>0)的渐近线方程为y=±3x，则双曲线的离心率是（ ）‎ A. B. C. D. 3‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 由渐近线求得，由双曲线的离心率求得答案.‎ - 29 -‎ ‎【详解】因为该双曲线的渐近线方程为y=±3x，则，‎ 所以双曲线的离心率 故选：A ‎【点睛】本题考查求双曲线的离心率，涉及双曲线的渐近线方程，属于简单题.‎ ‎3.若直线y=ax+2a与不等式组表示的平面区域有公共点，则实数a的取值范围是（ ）‎ A. [0，] B. [0，9] C. [0，+ ∞] D. 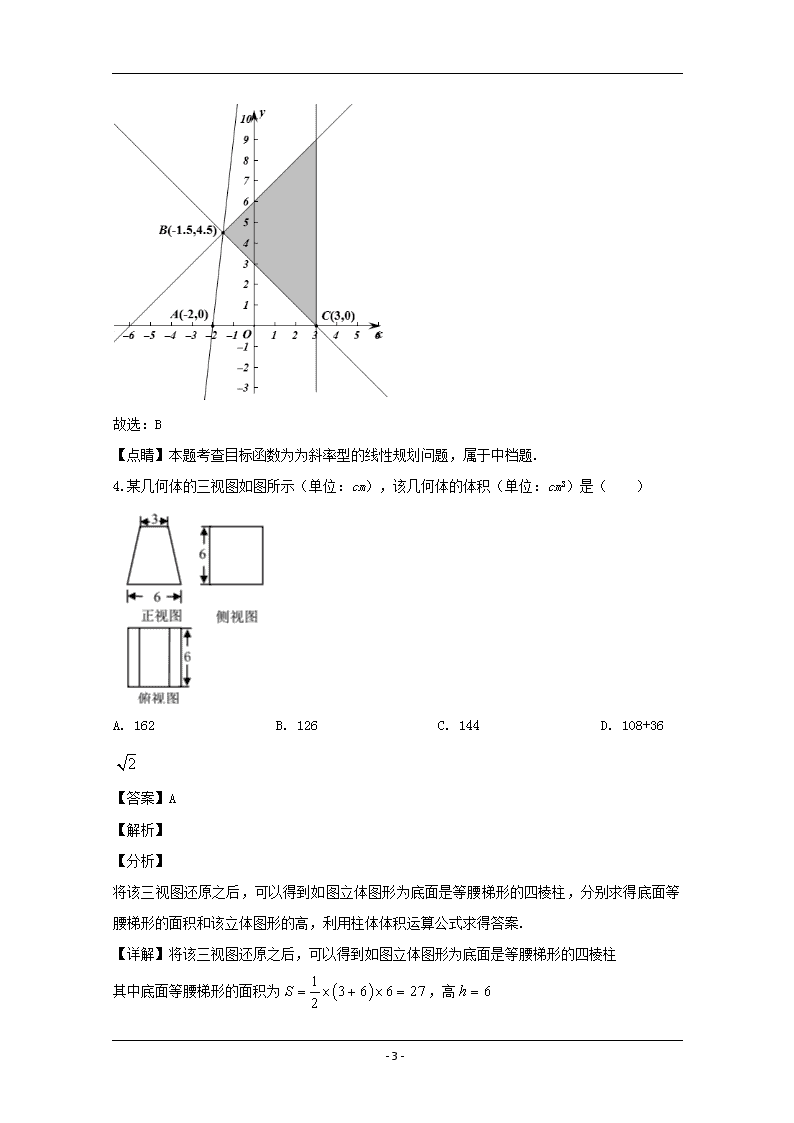[-∞，9]‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 作出满足已知约束条件的可行域，将目标函数转化为，其等价于可行域中任意一点与的直线的斜率，则，联立直线方程求得临界点坐标，由两点坐标求出，，可得答案.‎ ‎【详解】作出满足已知约束条件的可行域，将目标函数y=ax+2a转化为 其等价于可行域中任意一点与的直线的斜率，则 显然，，所以 - 29 -‎ 故选：B ‎【点睛】本题考查目标函数为为斜率型的线性规划问题，属于中档题.‎ ‎4.某几何体的三视图如图所示（单位：cm），该几何体的体积（单位：cm3）是（ ）‎ A. 162 B. 126 C. 144 D. 108+36‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 将该三视图还原之后，可以得到如图立体图形为底面是等腰梯形的四棱柱，分别求得底面等腰梯形的面积和该立体图形的高，利用柱体体积运算公式求得答案.‎ ‎【详解】将该三视图还原之后，可以得到如图立体图形为底面是等腰梯形的四棱柱 其中底面等腰梯形的面积为，高 - 29 -‎ 所以四棱柱的体积 故选：A ‎【点睛】本题考查立体几何中三视图还原求体积问题，属于中档题.‎ ‎5.已知平面α⊥平面β，且α∩β=l，aα，bβ，则“a⊥b”是“a⊥l或b⊥l”的（ ）‎ A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据线线垂直、线面垂直和面面垂直的相互转化，可证得条件可推结论，结论可推条件，即为充要条件.‎ ‎【详解】若有任意cα，且c⊥l，则，又因为平面α⊥平面β，即；‎ 若a⊥b，当a⊥l时显然成立，‎ 当a与l相交时，a与c也应相交，且，则，因为平面α⊥平面β，则b⊥l.‎ 所以若“a⊥b”则“a⊥l或b⊥l”‎ - 29 -‎ 若a⊥l或b⊥l，因为平面α⊥平面β，且α∩β=l，aα，bβ，所以或，‎ 由线面垂直的性质知a⊥b；‎ 所以“a⊥b”是“a⊥l或b⊥l”的充要条件.‎ 故选：C ‎【点睛】本题在充分必要性的判定下考查空间中垂直关系的推理，属于中档题.‎ ‎6.函数的图象可能是（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 当时，逐步分析到，显然此时，观察图像即可选出答案.‎ ‎【详解】当时，，所以，即 所以，所以 所以当时，，可排除ABC 故选：D ‎【点睛】本题考查由函数解析式选函数图象，属于中档题.‎ ‎7.已知0 D. D(X)=D(Y)‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 在分布列中由数学期望与方差的运算公式分别计算X与Y的对应值，既得答案.‎ ‎【详解】有题意知，分别的数学期望为，‎ ‎，‎ 分别的方差为，‎ 显然，D(X)=D(Y).‎ 故选：D ‎【点睛】本题考查分布列中计算数学期望与方差，属于中档题.‎ ‎8.已知C为Rt△ABD斜边BD上一点，且△ACD为等边三角形，现将△ABC沿AC翻折至.若在三棱锥中，直线和直线与平面ACD所成角分别为α，β，则（ ）‎ - 29 -‎ A. 0<α<β B. β<α≤2β C. 2β≤α≤3β D. α≥3β ‎【答案】B ‎【解析】‎ ‎【分析】‎ 在Rt△ABD中，△ACD为等边三角形，所以点C为BD中点，且,所以，过作面于点O，表示，则，由，得，假设，证得矛盾，即可说明假设不成立，原命题成立，即，即得答案.‎ ‎【详解】在Rt△ABD中，△ACD为等边三角形，所以点C为BD中点，且,所以 令,过作面于点O 所以，则且，所以 显然当时，则，显然成立 假设，则 - 29 -‎ ‎，矛盾，假设不成立，则 所以β<α≤2β 故选：B ‎【点睛】本题考查空间中折叠问题，涉及线面角的表示、运算与讨论，属于难题.‎ ‎9.已知00）上一点R(m，2)到它的准线的距离为3.若点A，B，C分别在抛物线上，且点A、C在y轴右侧，点B在y轴左侧，△ABC的重心G在y轴上，直线AB交y轴于点M且满足3|AM|<2|BM|，直线BC交y轴于点N.记△ABC，△AMG，△CNG的面积分别为S1，S2，S3.‎ - 29 -‎ ‎（1）求p的值及抛物线的准线方程；‎ ‎（2）求的取值范围.‎ ‎【答案】（1），；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）由抛物线x2=2py（p>0）上一点R(m，2)到它的准线的距离为3构建方程，求得p，则可得准线方程；‎ ‎（2）设点，，由面积公式可知由点G为的重心，且在y轴上，可以表示，由相似三角形可知，即可表示，令，整理得，由，得将视为二次函数求得值域，进而求得的范围，取倒即可得答案.‎ ‎【详解】（1）有题意知，，，所以准线方程：‎ ‎（2）设点，‎ - 29 -‎ 点G为的重心，且在y轴上，‎ 所以，且，则，且由相似三角形可知 所以 令，‎ 因为，所以，故，则 故 ‎【点睛】本题考查在抛物线的背景下探究平面图形面积比的范围问题，涉及求抛物线的标准方程，还考查了三角形重心的性质，属于难题.‎ ‎22.已知函数f(x)=(e-k)elnx+kx，其中k>0，g(x)=ex.‎ ‎（1）求函数f(x)的单调区间；‎ ‎（2）证明：当eg(x0).‎ ‎（注：e=2.71828L为自然对数的底数，且ln2≈0.693，ln3≈1.099.）‎ - 29 -‎ ‎【答案】（1）当时，增区间为；当，减区间为，增区间为（2）证明见解析 ‎【解析】‎ ‎【分析】‎ ‎（1）确定定义域，对函数f(x)求导，利用分类讨论求含参函数的单调区间的方式，表示单调区间；‎ ‎（2）需满足当eg(x0)；利用分类讨论思想，验证当时，显然成立，当时，对作差构建函数，令，由是关于的一次函数，所以，分别说明其中，，即，，不符合题意；当时，构造利用求导分析单调性为在区间上单调递增，即，，综上可得证.‎ ‎【详解】（1）由题意知，定义域为，且导函数.‎ 若，，函数在区间上单调递增； ‎ 若，由.‎ 当时，，此时函数单调递减 ‎ 当时，，此时函数单调递增.‎ ‎（2）当时，，即存在使得.‎ 当时，，令，整理得，因为是关于的一次函数，所以，其中，‎ - 29 -‎ ‎，又，‎ 所以，即，则不符合题意. ‎ 解法1：因为讨论的是整数解问题，所以接下来若能证明时，不符合题意即可.‎ 当时，令. ‎ 则，令，则，由易知在上单调递增，则，‎ 则在区间上单调递增，‎ ‎，即，‎ 则在区间上单调递增，则 ‎，即，不符合题意.综上所述，当时，存在唯一的整数，使得.‎ 解法2（评分标准参考解法1）：因为讨论的是整数解问题，所以接下来若能证明时，不符合题意即可.‎ 当时，令.则，令 ‎，则，由易知在上单调递增，则，则在区间上单调递增，则，即，则 - 29 -‎ 在区间上单调递增，则，即，不符合题意.‎ 综上所述，当时，存在唯一的整数，使得.‎ ‎【点睛】本题考查利用导数解决函数的综合问题，涉及利用导数求含参函数的单调区间问题，还考查了不等式整数解的分类讨论，属于难题.‎ - 29 -‎ ‎ ‎ - 29 -‎