高中数学必修1教案：第四章（第26课时）函数y=Asin(ωx+φ）的图象（1） 5页

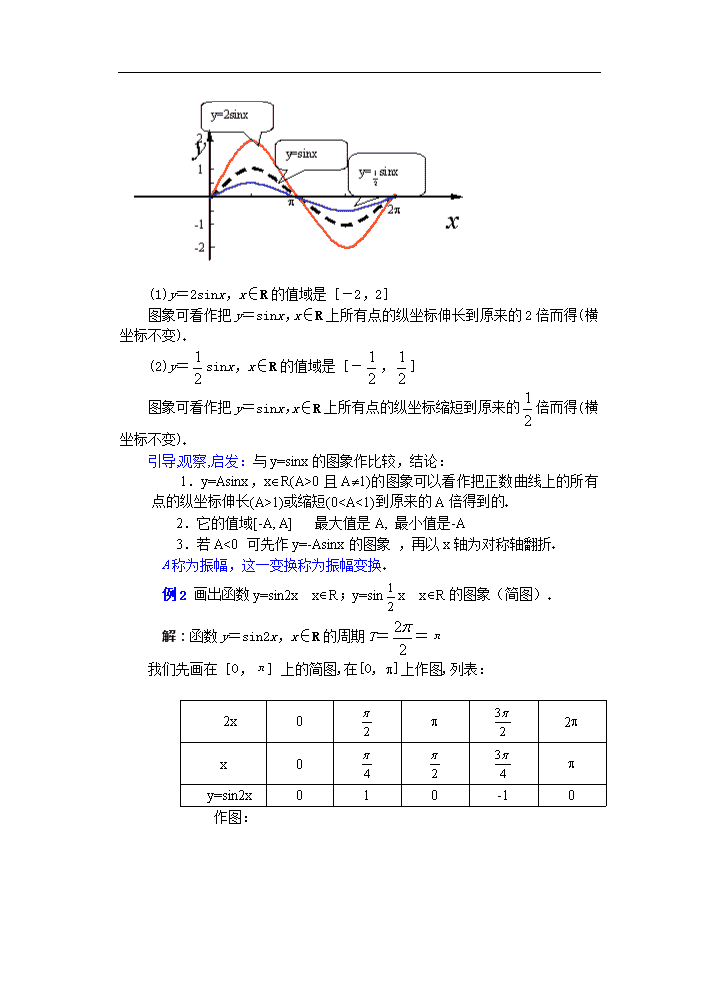
课 题：49函数y=Asin(ωx+φ) 的图象（1）‎ 教学目的：‎ ‎1理解振幅的定义；‎ ‎2理解振幅变换和周期变换的规律;‎ ‎3会用五点法画出函数y=Asinx和y=Asinωx的图象，明确A与ω对函数图象的影响作用；并会由y=Asinx的图象得出y=Asinx和y=Asinωx的图象 教学重点：熟练地对y＝sinx进行振幅和周期变换 教学难点：理解振幅变换和周期变换的规律 授课类型：新授课 课时安排：1课时 教 具：多媒体、实物投影仪 教学过程：‎ 一、复习引入：在现实生活中，我们常常会遇到形如y＝Asin(ωx＋)的函数解析式(其中A，ω，都是常数)下面我们讨论函数y＝Asin(ωx＋)，x∈R的简图的画法 二、讲解新课： ‎ 例1画出函数y=2sinx xÎR；y=sinx xÎR的图象（简图）‎ 解：画简图，我们用“五点法”‎ ‎∵这两个函数都是周期函数，且周期为2π ‎∴我们先画它们在［0，2π］上的简图列表：‎ x ‎ 0‎ p ‎2p ‎ sinx ‎ 0‎ ‎ 1‎ ‎ 0‎ ‎ -1‎ ‎ 0‎ ‎ 2sinx ‎ 0‎ ‎ 2‎ ‎ 0‎ ‎ -2‎ ‎0‎ ‎ sinx ‎ 0‎ ‎0‎ ‎-‎ ‎0‎ 作图：‎ ‎(1)y＝2sinx，x∈R的值域是［－2，2］‎ 图象可看作把y＝sinx，x∈R上所有点的纵坐标伸长到原来的2倍而得(横坐标不变)‎ ‎(2)y＝sinx，x∈R的值域是［－，］‎ 图象可看作把y＝sinx，x∈R上所有点的纵坐标缩短到原来的倍而得(横坐标不变)‎ 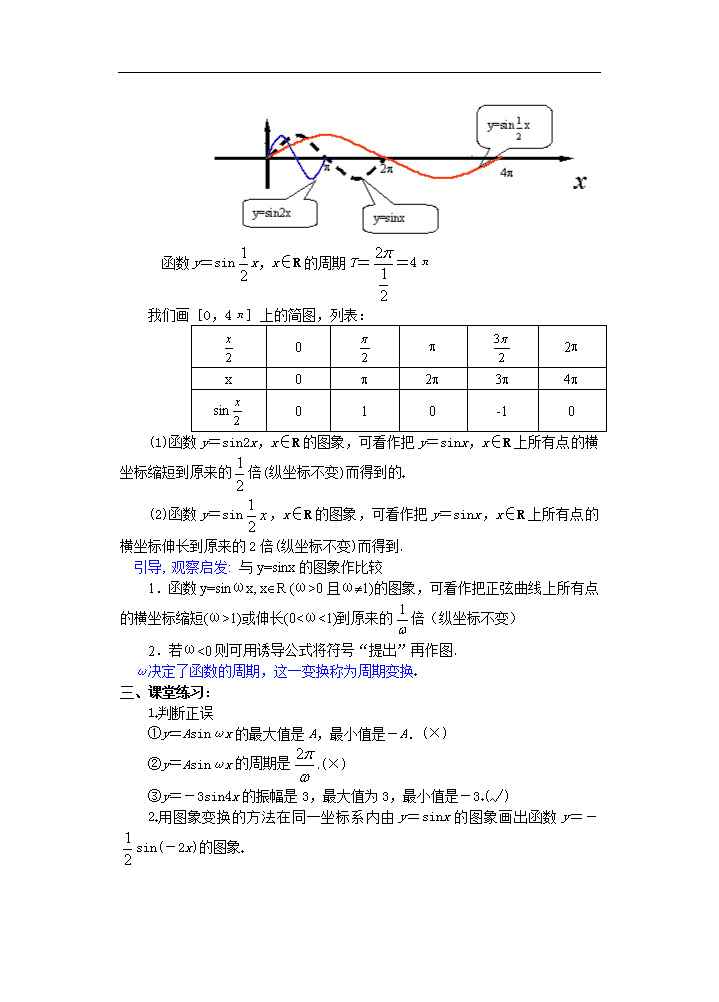引导,观察,启发：与y=sinx的图象作比较，结论：‎ ‎1．y=Asinx，xÎR(A>0且A¹1)的图象可以看作把正数曲线上的所有点的纵坐标伸长(A>1)或缩短(00且ω¹1)的图象，可看作把正弦曲线上所有点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的倍（纵坐标不变）‎ ‎2．若ω<0则可用诱导公式将符号“提出”再作图 ω决定了函数的周期，这一变换称为周期变换 三、课堂练习：‎ ‎1判断正误 ‎①y＝Asinωx的最大值是A，最小值是－A．(×)‎ ‎②y＝Asinωx的周期是(×)‎ ‎③y＝－3sin4x的振幅是3，最大值为3，最小值是－3(√)‎ ‎2用图象变换的方法在同一坐标系内由y＝sinx的图象画出函数y＝－sin(－2x)的图象 横坐标变为倍 纵坐标不变化 解：∵y＝－sin(－2x)＝sin2x作图过程，‎ 纵坐标变为倍 横坐标不变 y＝sinx y＝sin2x y＝sin2x 评述：先化简后画图 ‎3下列变换中，正确的是 A将y＝sin2x图象上的横坐标变为原来的2倍(纵坐标不变)即可得到 y＝sinx的图象 B将y＝sin2x图象上的横坐标变为原来的倍(纵坐标不变)即可得到 y＝sinx的图象 C将y＝－sin2x图象上的横坐标变为原来的倍,纵坐标变为原来的相反数,即得到y＝sinx的图象 D将y＝－3sin2x图象上的横坐标缩小一倍，纵坐标扩大到原来的倍，且变为相反数，即得到y＝sinx的图象 答案：A 四、小结 通过本节学习,要理解并学会对函数y＝sinx进行振幅和周期变换，即会画y＝Asinx，y＝sinωx的图象，并理解它们与y＝sinx之间的关系 五、课后作业：‎ ‎1如果y＝cosx是增函数，且y＝sinx是减函数，那么x的终边在( )‎ A第一象限 Ｂ第二象限 Ｃ第三象限 Ｄ第四象限 ‎2在［－π，π］上既是增函数，又是奇函数的是( )‎ Ay＝sinx Ｂy＝cosx Ｃy＝－sinx Ｄy＝sin2x ‎3函数y＝sin（－2x）的单调减区间是( )‎ ‎ ‎ ‎4函数y＝log2sinx的单调减区间是 ‎ ‎5函数f（x）＝cos2x＋2的递增区间是 ‎ ‎6若f（x）＝x2＋bx＋ｃ对任意实数x都有f（1＋x）＝f（1－x），则f（cos1）与f（cos）的大小关系是 ‎ 参考答案：1C 2A 3D ‎4［＋2kπ，π＋2kπ］，k∈Z ‎5［＋kπ，π＋kπ］，k∈Z ‎6f(cos1)＜f(cos)‎ 六、板书设计（略）‎ 七、课后记：‎ ‎ ‎