人教A版数学必修三1-1-2程序框图与算法的基本逻辑结构（3） 7页

第 3 课时 循环结构 （一）导入新课 思路 1（情境导入） 我们都想生活在一个优美的环境中，希望看到的是碧水蓝天，大家知道工厂的污水是怎 样处理的吗？污水进入处理装置后进行第一次处理，如果达不到排放标准，则需要再进入处 理装置进行处理，直到达到排放标准.污水处理装置是一个循环系统，对于处理需要反复操 作的事情有很大的优势.我们数学中有很多问题需要反复操作，今天我们学习能够反复操作 的逻辑结构——循环结构. 思路 2（直接导入） 前面我们学习了顺序结构，顺序结构像一条没有分支的河流，奔流到海不复回；上一节 我们学习了条件结构，条件结构像有分支的河流最后归入大海；事实上很多水系是循环往复 的，今天我们开始学习循环往复的逻辑结构——循环结构. （二）推进新课、新知探究、提出问题 （1）请大家举出一些常见的需要反复计算的例子. （2）什么是循环结构、循环体？ （3）试用程序框图表示循环结构. （4）指出两种循环结构的相同点和不同点. 讨论结果： （1）例如用二分法求方程的近似解、数列求和等. （2）在一些算法中，经常会出现从某处开始，按照一定的条件反复执行某些步骤的情况， 这就是循环结构.反复执行的步骤称为循环体. （3）在一些算法中要求重复执行同一操作的结构称为循环结构.即从算法某处开始，按照一 定条件重复执行某一处理的过程.重复执行的处理步骤称为循环体. 循环结构有两种形式：当型循环结构和直到型循环结构. 1°当型循环结构，如图（1）所示，它的功能是当给定的条件 P成立时，执行 A框，A 框执行完毕后，返回来再判断条件 P是否成立，如果仍然成立，返回来再执行 A框，如此 反复执行 A框，直到某一次返回来判断条件 P不成立时为止，此时不再执行 A框，离开循 环结构.继续执行下面的框图. 2°直到型循环结构，如图（2）所示，它的功能是先执行重复执行的 A框，然后判断 给定的条件 P是否成立，如果 P仍然不成立，则返回来继续执行 A框，再判断条件 P 是否 成立.继续重复操作，直到某一次给定的判断条件 P时成立为止，此时不再返回来执行 A框， 离开循环结构.继续执行下面的框图. 见示意图： 当型循环结构 直到型循环结构 (4)两种循环结构的不同点：直到型循环结构是程序先进入循环体，然后对条件进行判断， 如果条件不满足，就继续执行循环体，直到条件满足时终止循环. 当型循环结构是在每次执行循环体前，先对条件进行判断，当条件满足时，执行循环体， 否则终止循环. 两种循环结构的相同点: 两种不同形式的循环结构可以看出，循环结构中一定包含条件 结构，用于确定何时终止执行循环体. （三）应用示例 思路 1 例 1 设计一个计算 1+2+……+100的值的算法，并画出程序框图. 算法分析：通常，我们按照下列过程计算 1+2+……+100的值. 第 1步，0+1=1. 第 2步，1+2=3. 第 3步，3+3=6. 第 4步，6+4=10. …… 第 100步，4 950+100=5 050. 显然，这个过程中包含重复操作的步骤，可以用循环结构表示.分析上述计算过程，可 以发现每一步都可以表示为第（i-1）步的结果+i=第 i步的结果. 为了方便、有效地表示上述过程，我们用一个累加变量 S来表示第一步的计算结果， 即把 S+i的结果仍记为 S，从而把第 i步表示为 S=S+i， 其中 S的初始值为 0，i依次取 1，2，…，100，由于 i同时记录了循环的次数，所以也 称为计数变量. 解决这一问题的算法是： 第一步，令 i=1，S=0. 第二步，若 i≤100成立，则执行第三步；否则，输出 S，结束算法. 第三步，S=S+i. 第四步，i=i+1，返回第二步. 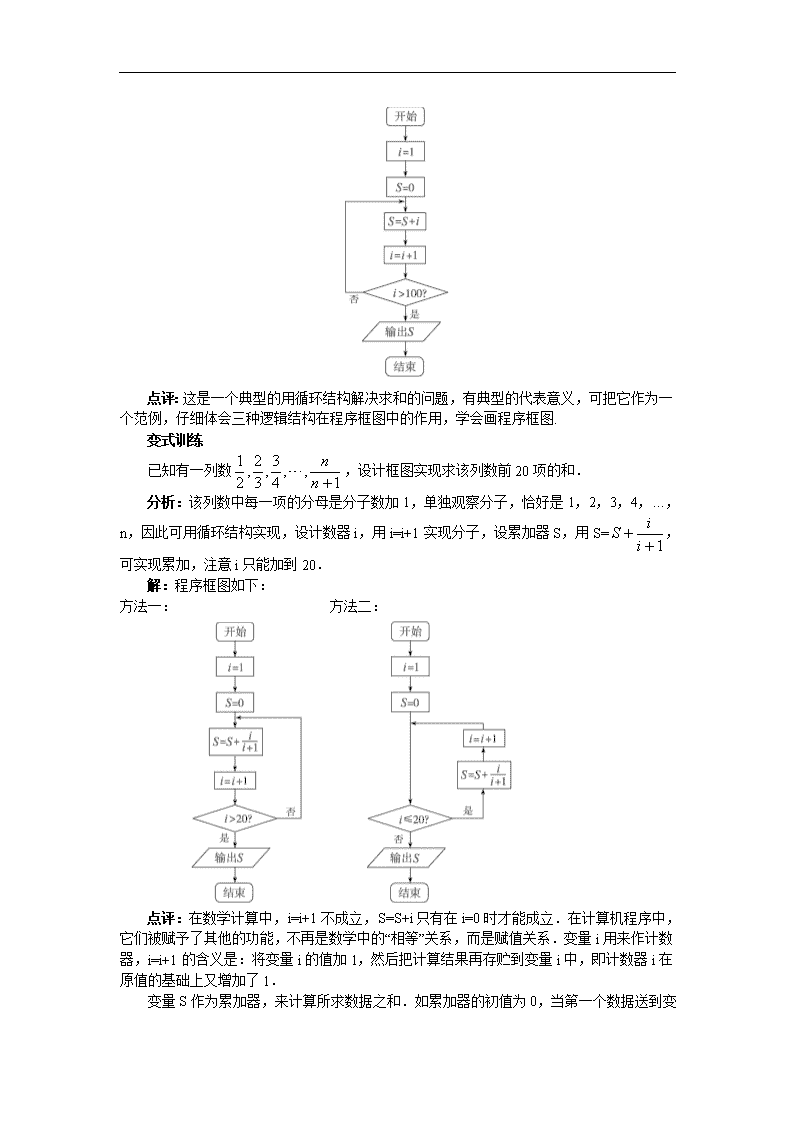程序框图如右： 上述程序框图用的是当型循环结构，如果用直到型循环结构表示，则程序框图如下： 点评：这是一个典型的用循环结构解决求和的问题，有典型的代表意义，可把它作为一 个范例，仔细体会三种逻辑结构在程序框图中的作用，学会画程序框图. 变式训练 已知有一列数 1 ,, 4 3, 3 2, 2 1 n n ，设计框图实现求该列数前 20项的和． 分析：该列数中每一项的分母是分子数加 1，单独观察分子，恰好是 1，2，3，4，…， n，因此可用循环结构实现，设计数器 i，用 i=i+1实现分子，设累加器 S，用 S= 1  i iS ， 可实现累加，注意 i只能加到 20． 解：程序框图如下： 方法一： 方法二： 点评：在数学计算中，i=i+1不成立，S=S+i只有在 i=0时才能成立．在计算机程序中， 它们被赋予了其他的功能，不再是数学中的“相等”关系，而是赋值关系．变量 i用来作计数 器，i=i+1的含义是：将变量 i的值加 1，然后把计算结果再存贮到变量 i中，即计数器 i在 原值的基础上又增加了 1． 变量 S作为累加器，来计算所求数据之和．如累加器的初值为 0，当第一个数据送到变 量 i中时，累加的动作为 S=S+i，即把 S的值与变量 i的值相加，结果再送到累加器 S中， 如此循环，则可实现数的累加求和． 例 2 某厂 2005年的年生产总值为 200万元，技术革新后预计以后每年的年生产总值都比 上一年增长 5%，设计一个程序框图，输出预计年生产总值超过 300万元的最早年份. 算法分析：先写出解决本例的算法步骤： 第一步，输入 2005年的年生产总值. 第二步，计算下一年的年生产总值. 第三步，判断所得的结果是否大于 300，若是，则输出该年的年份，算法结束；否则，返回 第二步. 由于“第二步”是重复操作的步骤，所以本例可以用循环结构来实现.我们按照“确定循环 体”“初始化变量”“设定循环控制条件”的顺序来构造循环结构. （1）确定循环体：设 a为某年的年生产总值，t为年生产总值的年增长量，n为年份，则循 环体为 t=0.05a,a=a+t,n=n+1. （2）初始化变量：若将 2005年的年生产总值看成计算的起始点，则 n的初始值为 2005，a 的初始值为 200. （3）设定循环控制条件：当“年生产总值超过 300万元”时终止循环，所以可通过判断“a>300” 是否成立来控制循环. 程序框图如下： 思路 2 例 1 设计框图实现 1+3+5+7+…+131的算法． 分析：由于需加的数较多，所以要引入循环结构来实现累加．观察所加的数是一组有规 律的数（每相临两数相差 2），那么可考虑在循环过程中，设一个变量 i，用 i=i+2 来实现这 些有规律的数，设一个累加器 sum，用来实现数的累加，在执行时，每循环一次，就产生一 个需加的数，然后加到累加器 sum中． 解：算法如下： 第一步，赋初值 i=1，sum=0. 第二步，sum=sum+i，i=i+2. 第三步，如果 i≤131，则反复执第二步；否则，执行下一步. 第四步，输出 sum. 第五步，结束． 程序框图如右图． 点评：（1）设计流程图要分步进行，把一个大的流程图分割成几个小的部分，按照三个 基本结构即顺序、条件、循环结构来局部安排，然后把流程图进行整合． （2）框图画完后，要进行验证，按设计的流程分析是否能实现所求的数的累加，分析条件 是否加到 131就结束循环，所以我们要注意初始值的设置、循环条件的确定以及循环体内语 句的先后顺序，三者要有机地结合起来．最关键的是循环条件，它决定循环次数，可以想一 想，为什么条件不是“i<131”或“i=131”，如果是“i<131”，那么会少执行一次循环，131就加 不上了． 例 2 高中某班一共有 40名学生，设计算法流程图，统计班级数学成绩良好(分数>80)和优 秀(分数>90)的人数． 分析：用循环结构实现 40个成绩的输入，每循环一次就输入一个成绩 s，然后对 s的值 进行判断.设两个计数器 m,n，如果 s>90，则 m=m+1，如果 80