2018年湖南省岳阳市高考二模数学文 18页

2018 年湖南省岳阳市高考二模数学文 一、选择题(本大题共 12 个小题，每小题 5 分，共 60 分.在每小题给出的四个选项中，只有 一项是符合题目要求的.) 1.已知集合 A={1，10， 1 10 }，B={y|y=lgx，x∈A}，则 A∩B=( ) A.{ 1 10 } B.{10} C.{1} D.∅ 解析：将集合 A 中的元素代入集合 B 中的函数 y=lgx 中，求出可对应 y 的值，确定出集合 B， 找出两集合的公共元素，即可求出两集合的交集. 将 x=1 代入得：y=lg1=0；将 x=10 代入得：y=lg10=1；将 x= 代入得：y=lg =-1， ∴集合 B={0，-1，1}，又 A={1，10， }， 则 A∩B={1}. 答案：C 2.已知 i 是虚数单位，复数 10 12 i i 的虚部为( ) A.-2 B.2 C.-2i D.2i 解析：求复数 10 12 i i 的虚部，首先把该复数分子分母同时乘以分母的共轭复数，化为实部加 虚部乘以 i 的形式，则虚部可求.       10 1 210 20 10 42 1 2 1 2 1 2 5          iiiii i i i ， 所以复数 的虚部为 2. 答案：B 3.设 x、y 满足约束条件 10 10 3          xy xy x ，则 z=2x-3y 的最小值是( ) A.-7 B.-6 C.-5 D.-3 解析：作出不等式组对应的平面区域，利用目标函数的几何意义，求出最优解即可求最小值. 由 z=2x-3y 得 2 33 y zx ， 作出不等式组对应的平面区域如图(阴影部分 ABC)： 平移直线 2 33 y zx ，由图象可知当直线 2 33 y zx ，过点 A 时，直线 2 33 y zx 截距 最大，此时 z 最小， 由 3 10      x xy 得 3 4    x y ，即 A(3，4)， 代入目标函数 z=2x-3y， 得 z=2×3-3×4=6-12=-6. ∴目标函数 z=2x-3y 的最小值是-6. 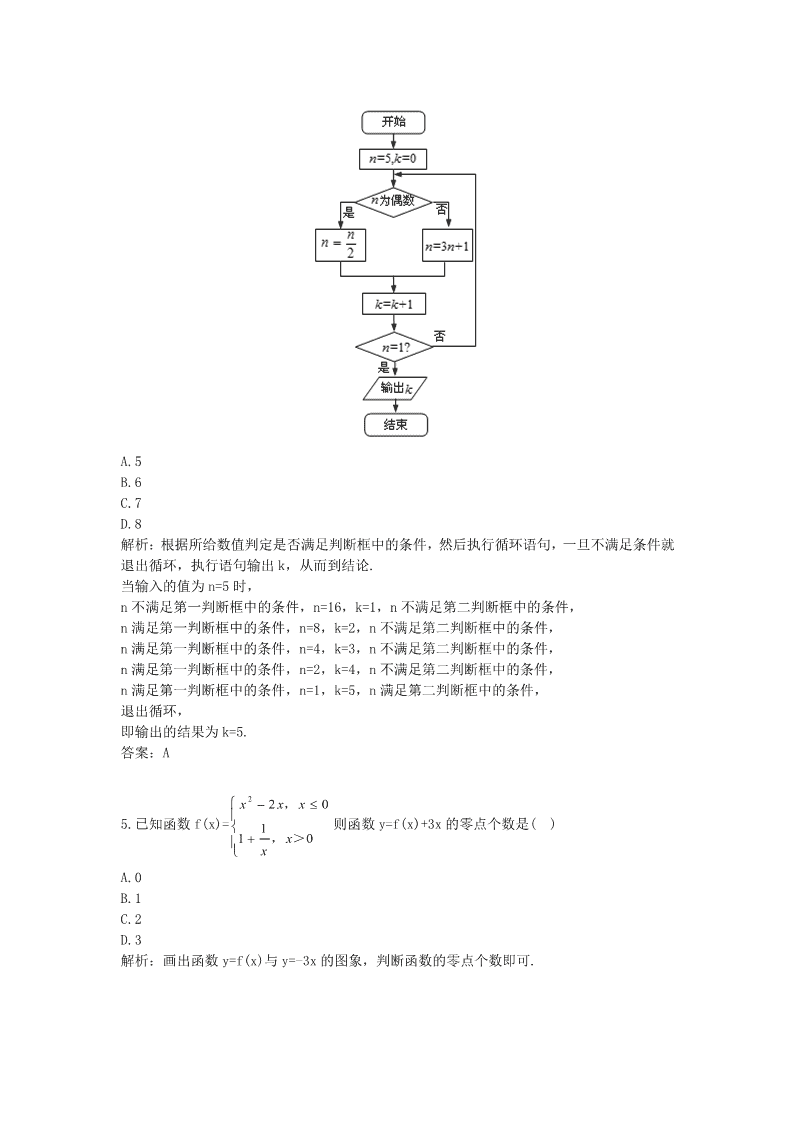答案：B 4.若程序框图如图所示，则该程序运行后输出 k 的值是( ) A.5 B.6 C.7 D.8 解析：根据所给数值判定是否满足判断框中的条件，然后执行循环语句，一旦不满足条件就 退出循环，执行语句输出 k，从而到结论. 当输入的值为 n=5 时， n 不满足第一判断框中的条件，n=16，k=1，n 不满足第二判断框中的条件， n 满足第一判断框中的条件，n=8，k=2，n 不满足第二判断框中的条件， n 满足第一判断框中的条件，n=4，k=3，n 不满足第二判断框中的条件， n 满足第一判断框中的条件，n=2，k=4，n 不满足第二判断框中的条件， n 满足第一判断框中的条件，n=1，k=5，n 满足第二判断框中的条件， 退出循环， 即输出的结果为 k=5. 答案：A 5.已知函数 f(x)= 2 20 110      ， ， ＞ x x x x x 则函数 y=f(x)+3x 的零点个数是( ) A.0 B.1 C.2 D.3 解析：画出函数 y=f(x)与 y=-3x 的图象，判断函数的零点个数即可. 函数 f(x)= 2 20 110      ， ， ＞ x x x x x ， 函数 y=f(x)+3x 的零点个数， 就是函数 y=f(x)与 y=-3x 两个函数的图象的交点个数： 如图： 由函数的图象可知，零点个数为 2 个. 答案：C 6.七巧板是我们祖先的一项创造，被誉为“东方魔板”，它是由五块等腰直角三角形(两块全 等的小三角形、一块中三角形和两块全等的大三角形)、一块正方形和一块平行四边形组成 的.如图是一个用七巧板拼成的正方形中任取一点，则此点取自黑色部分的概率是( ) A. 3 16 B. 3 8 C. 1 4 D. 1 8 解析：设边长 AB=2，求出△BCI 和平行四边形 EFGH 的面积，计算对应的面积比即可. 设 AB=2，则 BC=CD=DE=EF=1， ∴ 1 2 2 1 2 2 2 4    V BCIS ， 2 11 42 2   V平 行 四 边 形 BCIEFGHSS ， ∴所求的概率为 3 2 16 11 42 2       V 平 行 四 边 形 正 方 形 BCI EFGH ABCD SS P S . 答案：A 7.“直线 m 与平面α 内无数条直线平行”是“直线 m∥平面α ”的( ) A.充要条件 B.充分不必要条件 C.必要不充分条件 D.既不充分也不必要条件 解析：利用线面平行的判定定理性质定理、充分必要条件即可判断出结论. 由“直线 m∥平面α ”，可得“直线 m 与平面α 内无数条直线平行”，反之不成立. ∴“直线 m 与平面α 内无数条直线平行”是“直线 m∥平面α ”的必要不充分条件. 答案：C 8.若将函数 y=sin2x 的图象向左平移 6  个单位长度，则平移后图象的对称轴方程为( ) A. 2 12 kx (k∈Z) B. 22 kx (k∈Z) C. 2  kx (k∈Z) D. 2 12 kx (k∈Z) 解析：利用函数 y=Asin(ω x+φ )的图象变换规律，正弦函数的图象的对称性，得出结论. 将函数 y=sin2x 的图象向左平移 个单位长度，则平移后图象对应的函数解析式为 y=sin(2x+ 3  )， 令 2 32   xk，求得 2 12 kx ，k∈Z，故所得图象的对称轴方程为 2 12 kx ， k∈Z. 答案：D 9.已知一个简单几何的三视图如图所示，若该几何体的体积为 24π +48，则该几何体的表面 积为( ) A.24π +48 B.24π +90+6 41 C.48π +48 D.24π +66+6 41 解析：由题意，直观图为 1 4 圆锥与三棱锥的组合体， 该几何体的体积为 21 1 1 19 4 3 3 4 24 4 3 8 4 3 2           r r r r r ，∴r=2， ∴该几何体的表面积为 1 1 1 1 12 2 2 4 2 12 8 6 82 36 6 6 6 10 24 66 6 4 4 1                 . 答案：D 10.函数 2 ln  xx y x 的图象大致是( ) A. B. C. D. 解析：根据掌握函数的奇偶性和函数的单调性即可判断. 当 x＞0 时，y=xlnx，y′=1+lnx， 即 0＜x＜ 1 e 时，函数 y 单调递减，当 x＞ 1 e ，函数 y 单调递增， 因为函数 y 为偶函数. 答案：D 11.在 1 和 17 之间插入 n 个数，使这 n+2 个数成等差数列，若这 n 个数中第一个为 a，第 n 个为 b，当 1 25 ab 取最小值时，n=( ) A.4 B.5 C.6 D.7 解析：利用等差数列的性质可得 a+b=18，再利用“乘 1 法”与基本不等式的性质即可得出. 由已知得 a+b=1+17=18， 则  1 25 1 25 1 25 125 1 26 10 2 18 18 18                     a b a b a b a b b a ， 当且仅当 b=5a 时取等号，此时 a=3，b=15，可得 n=7. 答案：D 12.已知函数   ln 2 x axfx x ，若有且仅有一个整数 k，使得 f(k)＞1，则实数 a 的取值 范围是( ) A.(1，3] B.[ 1 4 ln 2 1 2  ， 1 6 ln 3 1 2  ) C.[ 1 2 ln 2 1 ， 1 3 ln 3 1 ) D.( 1 e -1，e-1] 解析：由 ln 2 1 ＞x ax x ，得 ln21 ＜ xa x ， 令 g(x)= ln x x ，则 g′(x)= 2 1 ln x x ， 令 g′(x)＞0，解得：0＜x＜e， 令 g′(x)＜0，解得：x＞e， 故 g(x)在(0，e)递增，在(e，+∞)递减， 而 g(2)= ln 2 2 ≈0.345，g(3)= ln 3 3 ≈0.366， 故 g(3)＞g(2)， 故 g(2)≤2a+1＜g(3)， 故 1 1 1 1 4 2 6 2 ln 2 ln 3  ＜a . 答案：B 二、填空题(本大题共 4 小题，每小题 5 分，共 20 分，将正确答案填在答题卡的横线上) 13.若数列{an}满足 a1=1，a2= 1 2 ，an+1 2=an·an+2(n∈N*)，则数列{an}的前 n 项和 Sn= . 解析：利用等比数列的定义、求和公式即可得出. ∵数列{an}满足 a1=1，a2= ，an+1 2=an·an+2(n∈N*)， ∴数列{an}是等比数列，公比 2 1 1 2 aq a . 可得前 n 项和 1 21 1 12 1 21 2         n n nS . 答案： 2 21 1   n 14.已知 f(x)=f(4-x)，当 x≤2 时，f(x)=ex，f′(3)+f(3)= . 解析：由 f(x)=f(4-x)可得， 函数 f(x)的图象关于直线 x=2 对称， 当 x≤2 时，f(x)=ex，f′(x)=ex， ∴f(3)=f(1)=e， f′(3)=-f′(1)=-e， 故 f′(3)+f(3)=0. 答案：0 15.已知抛物线 y=ax2(a＞0)的准线为 l，l 与双曲线 2 2 1 4 x y 的两条渐近线分别交于 A，B 两点，若|AB|=4，则 a= . 解析：抛物线 y=ax2(a＞0)的准线 l：y= 1 4  a ， 双曲线 的两条渐近线分别为 y= 1 2 x，y= 1 2  x， 可得 xA= 1 2  a ，xB= 1 2a ，可得|AB|= 11 22     aa =4，则 a= 1 4 . 答案： 1 4 16.直线 ax+by+c=0 与圆 O：x2+y2=16 相交于两点 M、N，若 c2=a2+b2，P 为圆 O 上任意一点， 则 uuur g uuur P PNM 的取值范围是 . 解析：取 MN 的中点 A，连接 OA，则 OA⊥MN.由点到直线的距离公式算出 OA=1，从而在 Rt△ AON 中，得到 cos∠AON= 1 4 ，得 cos∠MON= 7 8  ，最后根据向量数量积的公式即可算出 uuur uuur gOM ON 的值，运用向量的加减运算和向量数量积的定义，可得 uuur uuur gPM PN =2-8cos∠AOP， 考虑 uuur OP ， uur OA同向和反向，可得最值，即可得到所求范围. 取 MN 的中点 A，连接 OA，则 OA⊥MN， ∵c2=a2+b2， ∴O 点到直线 MN 的距离 22 1  c OA ab ， x2+y2=16 的半径 r=4， ∴Rt△AON 中，设∠AON=θ ，得cos 1 4  OA ON ， 2cos cos 2 2 cos 171 88 1     M ON ， 由此可得， cos 4 8 4 147        uuur uuur uuur uuur ggOM ON OM NON MO ， 则      2        uuur uuur uuur uuur uuur uuur uuur uuur uuuuuu r uur g g g g ur uuur PM OM OP ON OP OM ON OP OP OM ONPN 14 16 2 2 2 2 o8cos c s          uuur uuuruur uur ggO P O P AOOA POA AO P ， 当 uuur OP ， uur OA同向时，取得最小值且为 2-8=-6， 当 ， 反向时，取得最大值且为 2+8=10. 则 uuur g uuur P PNM 的取值范围是[-6，10]. 答案：[-6，10] 三、解答题(本大题共 6 小题，共 70 分，第 17~21 题为必考题，每小题 12 分，第 22、23 题为选考题，有 10 分.解答应写出文字说明、证明过程或演算步骤.) 17.已知函数   2sin3 sin cosf x x x x . (1)求函数 f(x)的最小正周期. 解析：(1)利用三角恒等变换化简函数的解析式，利用三角函数的周期公式即可得解. 答案：(1) ∵   2sin sin cos cos 2 sin 23 3 1 33 2 2 2 sin 2 3 2            f x x x x x x x ， ∴函数 f(x)的最小正周期 T= 2 2  =π . (2)已知△ABC 的内角 A，B，C 的对边分别为 a，b，c，若 3 22  Af ，a=4，b+c=5，求△ ABC 的面积. 解析：(2)由 求得 A 的值，利用余弦定理求得 bc 的值，可得△ABC 的面积 S= 1 2 bc·sinA 的值. 答案：(2)∵ 3n 23 3 2 si 2              AfA ， ∴sin 0 3  A ， ∴A- 3  =0， ∴A= 3  ， 又∵a=4，b+c=5， ∴a2=b2+c2-2bc·cosA=(b+c)2-3bc=25-3bc=16， ∴bc=3， ∴△ABC 的面积 sin 31 1 3 3 3 2 2 2 4     gS bc A . 18.某校高二奥赛班 N 名学生的物理测评成绩(满分 120 分)分布直方图如图，已知分数在 100-110 的学生数有 21 人. (1)求总人数 N 和分数在 110-115 分的人数 n. 解析：(1)求出该班总人数、分数在 110-115 内的学生的频率，即可得出分数在 110-115 内 的人数. 答案：(1)分数在 100-110 内的学生的频率为 P1=(0.04+0.03)×5=0.35， 所以该班总人数为 N= 21 0.35 =60， 分数在 110-115 内的学生的频率为 P2=1-(0.01+0.04+0.05+0.04+0.03+0.01)×5=0.1，分数 在 110-115 内的人数 n=60×0.1=6. (2)现准备从分数在 110-115 的 n 名学生(女生占 1 3 )中任选 2 人，求其中恰好含有一名女生 的概率. 解析：(2)利用列举法确定基本事件的个数，即可求出其中恰好含有一名女生的概率. 答案：(2)由题意分数在 110-115 内有 6 名学生，其中女生有 2 名， 设男生为 A1，A2，A3，A4，女生为 B1，B2， 从 6 名学生中选出 3 人的基本事件为： (A1，A2)，(A1，A3)，(A1，A4)，(A1，B1)，(A1，B2)， (A2，A3)，(A2，A4)，(A2，B1)，(A2，B2)，(A3，A4)， (A3，B1)，(A3，B2)，(A4，B1)，(A4，B2)，(B1，B2)共 15 个. 其中恰 好含有一名女生的基本事件为 (A1，B1)，(A1，B2)，(A2，B2)，(A2，B1)，(A3，B1)， (A3，B2)，(A4，B1)，(A4，B2)，共 8 个， 所以所求的概率为 P= 8 15 . (3)为了分析某个学生的学习状态，对其下一阶段的学生提供指导性建议，对他前 7 次考试 的数学成绩 x(满分 150 分)，物理成绩 y 进行分析，下面是该生 7 次考试的成绩. 已知该生的物理成绩y 与数学成绩x是线性相关的，求出y关于x的线性回归方程 y bx a$ $ $ . 若该生的数学成绩达到 130 分，请你估计他的物理成绩大约是多少？ (参考公式：       1 2 1        $ n ii i n i i x x y y b xx ， a y b x$$) 解析：(3)分别求出回归学生的值，代入从而求出线性回归方程，将 x=130 代入，从而求出 y 的值. 答案：(3) x =100， y =100； 由于 x 与 y 之间具有线性相关关系，根据回归系数公式得到 497 0.5 994 $b ，$a =100-0.5×100=50， ∴线性回归方程为$y =0.5x+50， ∴当 x=130 时，$y =115. 19.如图，多面体 ABCDEF 中，四边形 ABCD 为菱形，且∠DAB=60°，EF∥AC，AD=2，EA=ED=EF= 3 . (1)求证：AD⊥BE. 解析：(1)取 AD 中点 O，连结 EO，BO.证明 EO⊥AD.BO⊥AD.说明 AD⊥平面 BEO，即可证明 AD ⊥BE. 答案：(1)如图，取 AD 中点 O，连结 EO，BO. ∵EA=ED，∴EO⊥AD. ∵四边形 ABCD 为菱形， ∴AB=AD， 又∠DAB=60°，∴△ABD 为等边三角形，∴BA=BD， ∴BO⊥AD. ∵BO∩EO=O，BO  平面 BEO，EO 平面 BEO，∴AD⊥平面 BEO， ∵BE  平面 BEO，∴AD⊥BE. (2)若 BE= 5 ，求三棱锥 F-BCD 的体积. 解析：(2)解法一：证明 EO⊥OB，然后证明 EO⊥平面 ABCD.通过 VF-BCD=VE-BCD 求解即可. 解法二：解法二：证明 EO⊥OB，利用 AD⊥平面 EOB，以及 VF-BCD=VE-BCD=VE-ABD 求解即可. 答案：(2)解法一：在△EAD 中，EA=ED= ，AD=2， ∴ 222  EO AE AO ， ∵△ABD 为等边三角形，∴AB=BD=AD=2，∴BO= 3 . 又 BE= 5 ，∴EO2+OB2=BE2，∴EO⊥OB， ∵AD∩OB=O，AD  平面 ABCD，BO 平面 ABCD， ∴EO⊥平面 ABCD. 又 1133 2 2 2     V ggABDS AD OB ， ∴S△BCD=S△ABD= 3 . 又∵EF∥AC， ∴ 63 3 33 211      V gF BCD E BCD BCDV V S EO . 解法二：在△EAD 中，EA=ED= 3 ，AD=2， ∴ 222  EO AE AO ， ∵△ABD 为等边三角形， ∴AB=BD=AD=2，∴BO= 3 . 又 BE= 5 ，∴EO2+OB2=BE2，∴EO⊥OB， 所以 11 2 62 2 3 2     V ggEOBS EO OB . 又 S△BCD=S△ABD，EF∥AC，AD⊥平面 EOB， ∴ 11 3 2 23 66 3      V gF BCD E BCD E ABD EOBV V V S AD . 20.如图，A，B 是椭圆 C： 2 2 1 4 x y 长轴的两个端点，P，Q 是椭圆 C 上都不与 A，B 重合 的两点，记直线 BQ，AQ，AP 的斜率分别是 kBQ，kAQ，kAP. (1)求证：kBQ·kAQ= 1 4  . 解析：(1)设 Q(x1，y1)，由题意方程求出 A，B 的坐标，代入斜率公式即可证明 kBQ·kAQ= . 答案：(1)证明：设 Q(x1，y1)， 由椭圆 C： 2 2 1 4 x y ，得 B(-2，0)，A(2，0)， ∴ 2 1 2 1 1 1 22 1 1 1 1 1 4 2 2 4 1 4 4           ggBQ AQ x y y ykk x x x x . (2)若 kAP=4kBQ，求证：直线 PQ 恒过定点，并求出定点坐标. 解析：(2)由(1)结合 kAP=4kBQ，可得 kAP·kAQ=-1，设 P(x2，y2)，直线 PQ：x=ty+m，联立直线 方程与椭圆方程，利用根与系数的关系及 kAP·kAQ=-1 列式求得 m 值，则可证明直线 PQ 恒过 定点，并求出定点坐标. 答案：(2)由(1)知： 1 4 BQ BQkk 11 44 gAP AQkk kAP·kAQ=-1. 设 P(x2，y2)，直线 PQ：x=ty+m， 代入 x2+4y2=4，得(t2+4)y2+2mty+m2-4=0， ∴ 122 2 4   mtyy t ， 2 12 2 4 4   myy t ， 由 kAP·kAQ=-1 得：(x1-2)(x2-2)+y1y2=0， ∴(t2+1)y1y2+(m-2)t(y1+y2)+(m-2)2=0， ∴(t2+1)(m2-4)+(m-2)t(-2mt)+(m-2)2(t2+4)=0， ∴5m2-16m+12=0，解得 m=2 或 m= 6 5 . ∵m≠2，∴m= 6 5 ， ∴直线 PQ：x=ty+ 6 5 ，恒过定点( 6 5 ，0). 21.已知函数 f(x)=ax2+lnx+2. (1)若 a∈R，讨论函数 f(x)的单调性. 解析：(1)求出函数的导数，通过讨论 a 的范围，求出函数的单调区间即可. 答案：(1)   21 2 12     axf x ax xx ，(x＞0)， a≥0 时，恒有 f′(x)＞0，f(x)在(0，+∞)递增， a＜0 时，令 f′(x)＞0，即 2ax2+1＞0，解得：0＜x＜ 1 2  a ， 令 f′(x)＜0，即 2ax2+1＜0，解得：x＞ 1 2  a ， 综上，a≥0 时，f(x)在(0，+∞)递增， a＜0 时，f(x)在(0， 1 2  a )递增，在( 1 2  a ，+∞)递减. (2)曲线 g(x)=f(x)-ax2 与直线 l 交于 A(x1，y1)，B(x2，y2)，两点，其中 x1＜x2，若直线 l 斜率为 k，求证：x1＜ 1 k ＜x2. 解析：(2)问题等价于 2 1 21 2 1 1 1 ln  ＜ ＜ x x xxx x ，令 t= 2 1 x x ，则 t＞1，问题转化为只需证 1＜ 1 ln t t ＜ t，根据函数的单调性证明即可. 答案：(2)证明：    2121 2 1 2 1 ln ln   g x g x xxk x x x x ， 要证 x1＜ 1 k ＜x2，即证 21 12 21ln ln   ＜ ＜xxxx xx ， 等价于 2 1 21 2 1 1 1 ln  ＜ ＜ x x xxx x ， 令 t= ，则 t＞1，只需证 1＜ ＜t， 由 t＞1 知 lnt＞0，故等价于 lnt＜t-1＜tlnt， 设φ (t)=t-1-lnt，则φ ′(t)=1-1 t ＞0， 所以φ (t)在(1，+∞)上单增， 所以φ (t)＞φ (1)=0， 即 t-1＞lnt 又设 h(t)=tlnt-(t-1)， 则 h′(t)=lnt＞0， 所以 h(t)在(1，+∞)上单增， 所以 h(t)＞h(1)=0， 即 tlnt＞t-1， 故 x1＜ 1 k ＜x2. 请考生在 22、23 题中任选一题作答，如果多做，则按所做的第一题记分.作答时请写清题号. [选修 4-4：坐标系与参数方程] 22.已知曲线 C 的极坐标方程是ρ =2cosθ ，若以极点为平面直角坐标系的原点，极轴为 x 轴的正半轴，且取相同的单位长度建立平面直角坐标系，则直线 l 的参数方程是 3 2 1 2      x t m yt (t 为参数). (1)求曲线 C 的直角坐标方程与直线 l 的普通方程. 解析：(1)由 x=ρ cosθ ，y=ρ sinθ ，x2+y2=ρ 2，可得曲线 C 的普通方程；运用代入法，可 得直线 l 的普通方程. 答案：(1)由 x=ρ cosθ ，y=ρ sinθ ，x2+y2=ρ 2， 曲线 C 的极坐标方程是ρ =2cosθ ，即为ρ 2=2ρ cosθ ， 即有 x2+y2=2x，即圆(x-1)2+y2=1； 由直线 l 的参数方程是 (t 为参数)， 可得 x- 3 y-m=0. (2)设点 P(m，0)，若直线 l 与曲线 C 交于 A，B 两点，且|PA|·|PB|=1，求非负实数 m 的值. 解析：(2)将直线 l 的参数方程代入曲线的普通方程，运用判别式大于 0，韦达定理，结合 参数的几何意义，解方程，即可得到所求 m 的值. 答案：(2)将 代入圆(x-1)2+y2=1， 可得 t2+ (m-1)t+m2-2m=0， 由△=3(m-1)2-4(m2-2m)＞0，可得-1＜m＜3， 由 m 为非负数，可得 0≤m＜3. 设 t1，t2 是方程的两根，可得 t1t2=m2-2m， |PA|·|PB|=1，可得|m2-2m|=1， 解得 m=1 或1 2 ， 由 0≤m＜3.可得 m=1 或 1+ 2 . [选修 4-5：不等式选讲] 23.已知函数 f(x)=|2x+2|-|2x-2|，x∈R. (1)求不等式 f(x)≤3 的解集. 解析：(1)通过讨论 x 的范围，得到关于 x 的不等式组，求出不等式的解集即可. 答案：(1)原不等式等价于 1 43   ＜x 或 11 43      x x 或 1 43    ＞x ， 解得：x＜-1 或-1≤x≤ 3 4 ， ∴不等式 f(x)≤3 的解集为(-∞， 3 4 ]. (2)若方程   2  fx ax有三个实数根，求实数 a 的取值范围. 解析：(2)分离 a，得到 a=x+|x-1|-|x+1|，令 h(x)=x+|x-1|-|x+1|，结合函数的图象求出 a 的范围即可. 答案：(2)由方程 可变形为 a=x+|x-1|-|x+1|， 令   21 1 1 1 1 21              ， ＜ ， ， ＞ xx h x x x x x x xx ， 作出图象如下： 于是由题意可得-1＜a＜1.