【精品试卷】新高考2021届高三数学入学调研试题三(含解析） 18页

1 （新高考）2021 届高三数学入学调研试题（三） 注意事项： 1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形 码粘贴在答题卡上的指定位置。 2．选择题的作答：每小题选出答案后，用 2B 铅笔把答题卡上对应题目的答案标号涂 黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。 3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草 稿纸和答题卡上的非答题区域均无效。 4．考试结束后，请将本试题卷和答题卡一并上交。 第Ⅰ卷 一、单项选择题：本题共 8 小题，每小题 5 分，共 40 分．在每小题给出的四个选项中，只 有一项是符合题目要求的． 1．已知集合   24 2 { 6 0M x x N x x x       ， ，则 M N  （ ） A． { 4 3x x   B． { 4 2x x   C． { 2 2x x   D． { 2 3x x  2．已知 2 1 i(1 i) z   （i 为虚数单位），则复数 z  （ ） A．1 i B．1 i C． 1 i  D． 1 i  3．为了加强“精准扶贫”，实现伟大复兴的“中国梦”，某大学派遣甲、乙、丙、丁、戊五位同学参 加 、 、A B C 三个贫困县的调研工作，每个县至少去 1 人，且甲、乙两人约定去同一个贫困县，则 不同的派遣方案共有（ ）种． A．24 B．36 C．48 D．64 4．在边长为1的正方形 ABCD 中，M 为 BC 的中点，点 E 在线段 AB 上运动，则 EC EM  的取值 范围是（ ） A． 1 ,22      B． 30, 2      C． 1 3,2 2      D． 0,1 5．已知定义域为(－1，1)的奇函数 ( )y f x 又是减函数，且 2( 3) (9 ) 0f a f a    ，则 a 的取 值范围是（ ） A． (3, 10) B． (2 2,3) C． (2 2,4) D． ( 2,3) 6．已知四棱锥 P ABCD- 的四条侧棱都相等，底面是边长为 2 的正方形，若其五个顶点都在一个 表面积为 81π 4 的球面上，则 PA 与底面 ABCD 所成角的正弦值为（ ） A． 2 3 B． 2 3 或 5 3 C． 2 2 3 D． 1 3 或 2 2 3 7．二项式 8( )ax x  的展开式中 2x 的系数是 7 ，则 a （ ） A．1 B． 1 2 C． 1 2  D． 1 8．由国家公安部提出，国家质量监督检验检疫总局发布的《车辆驾驶人员血液、呼气酒精含量阀值 与检验标准（ GB / T19522 2010 ）》于 2011年 7 月1日正式实施．车辆驾驶人员酒饮后或者醉酒 后驾车血液中的酒精含量阀值见表．经过反复试验，一般情况下，某人喝一瓶啤酒后酒精在人体血 液中的变化规律的“散点图”见图， 喝1瓶啤酒的情况且图表示的函数模型   0.5 40sin 13, 0 23 90 14, 2 π x x xf x e x               ，则该人喝一瓶啤酒后 至少经过（ ）个小时才可以驾车（时间以整小时计算）？（参考数据：ln5 2.71 ，ln30 3.40 ） 驾驶行为类型 阀值 mg /100 mL 饮酒后驾车 20 ， 80 醉酒后驾车 80 车辆驾车人员血液酒精含量阀值 A． 5 B． 6 C． 7 D．8 二、多项选择题：本题共 4 小题，每小题 5 分，共 20 分．在每小题给出的选项中，有多项 符合题目要求．全部选对的得 5 分，部分选对的得 3 分，有选错的得 0 分． 9．已知双曲线 2 2 2 14 x y b   的右焦点与抛物线 2 12y x 的焦点 F 重合，则（ ） A．双曲线的实轴长为 2 B．双曲线的离心率为 3 C．双曲线的渐近线方程为 5 2y x  D．F 到渐近线的距离为 5 2 10．已知函数    sinf x A x   （其中 0A  ， 0 ， 0 π  的部分图象，则下列结论 正确的是（ ） A．函数  f x 的图象关于直线 π 2x  对称 B．函数  f x 的图象关于点 π ,012     对称 C．函数  f x 在区间 π π,3 6     上单调增 D．函数 1y  与   π 23π 12 12y f x x       的图象的所有交点的横坐标之和为 8π 3 11．已知 0a  ， 0b  ，且 1a b  ，则（ ） A． 2 2 1 2a b  B． 12 2 a b  C． 2 2log log 2a b   D． 2a b  12．“杂交水稻之父”袁隆平一生致力于杂交水稻技术的研究、应用与推广，发明了“三系法”籼型 杂交水稻，成功研究出“两系法”杂交水稻，创建了超级杂交稻技术体系，为我国粮食安全、农业 科学发展和世界粮食供给做出了杰出贡献；某杂交水稻种植研究所调查某地水稻的株高，得出株高 (单位：cm)服从正态分布，其密度曲线函数为       2100 2001 , , 10 2π x f x e x      ，则下列说法 正确的是（ ） A．该地水稻的平均株高为 100 cm B．该地水稻株高的方差为 10 C．随机测量一株水稻，其株高在 120 cm 以上的概率比株高在 70 cm 以下的概率大 D．随机测量一株水稻，其株高在(80，90)和在(100，110)(单位：cm)的概率一样大 第Ⅱ卷 三、填空题：本大题共 4 小题，每小题 5 分，共 20 分． 13．设O 为坐标原点，抛物线 2: 4C y x 的准线为l ，焦点为 F ，过 F 且斜率为 3 的直线与抛物 线C 交于 ,A B 两点，且| | | |AF BF ，若直线 AO 与l 相交与 D ，则 | | | | OF BD  _________． 14．任意实数 a，b，定义 , 0 , 0 ab ab a b a abb     ，设函数   lnf x x x  ，正项数列 na 是公比大 于 0 的 等 比 数 列 ， 且 1010 1a  ，          1 2 3 2019 2020f a f a f a f a f a e       ， 则 2020a  ______． 15．已知球的直径 4DC  ，A ，B 是该球面上的两点， π 6ADC BDC    ，则三棱锥 A BCD 的体积最大值是______． 16．如图，A 、B 是直线l 上的两点，且 2AB  ，两个半径相等的动圆分别与l 相切于 A 、B 两点， C 是这两个圆的公共点，则圆弧 AC ，圆弧CB 与线段 AB 围成图形面积 S 的取值范围是_________． 四、解答题：本大题共 6 个大题，共 70 分．解答应写出文字说明、证明过程或演算步骤． 17．（10 分）已知在 ABC△ 中， a ，b ， c 分别为角 A ， B ，C 的对应边，点 D 为边 BC 的中点， ABC△ 的面积为 2 2sin AD B ． （1）求sin sinBAD BDA   的值； （2）若 2BD AB ， 3AD  ，求b ． 3 18．（12 分）已知函数 ( ) logkf x x （k 为常数， 0k  且 1k  ）． （1）在下列条件中选择一个________使数列 na 是等比数列，说明理由． ①数列   nf a 是首项为 2，公比为 2 的等比数列； ②数列   nf a 是首项为 4，公差为 2 的等差数列； ③数列   nf a 是首项为 2，公差为 2 的等差数列的前 n 项和构成的数列． （2）在（1）的条件下，当 2k  时，设 1 2 2 4 1    n n na b n ，求数列 nb 的前 n 项和 nT ． 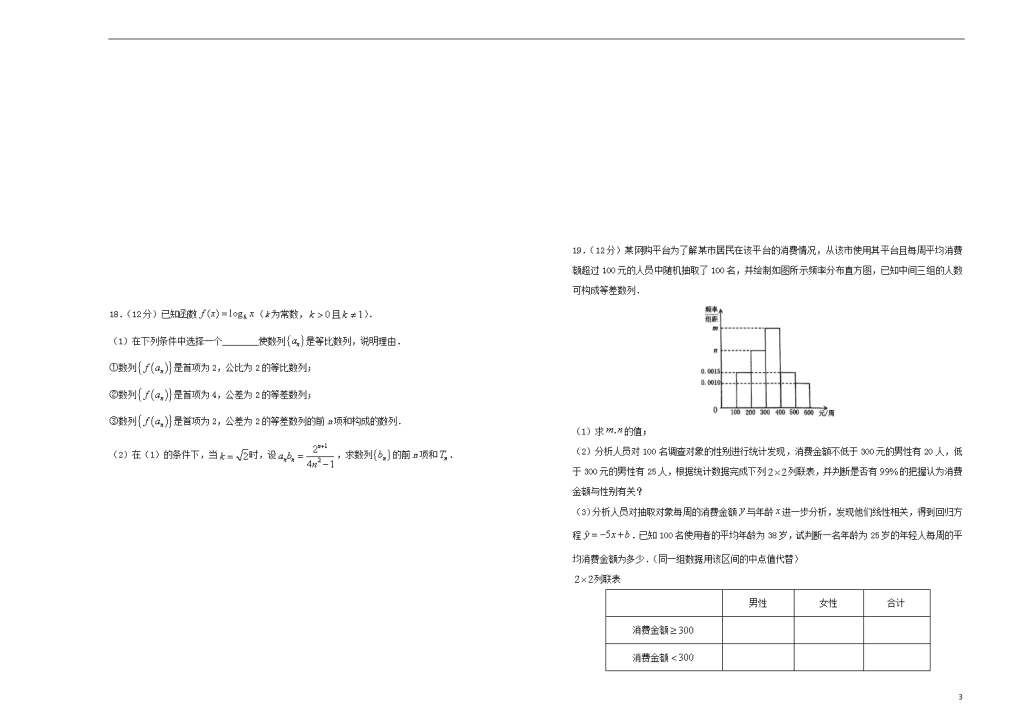19．（12 分）某网购平台为了解某市居民在该平台的消费情况，从该市使用其平台且每周平均消费 额超过 100 元的人员中随机抽取了 100 名，并绘制如图所示频率分布直方图，已知中间三组的人数 可构成等差数列． （1）求 ,m n 的值； （2）分析人员对 100 名调查对象的性别进行统计发现，消费金额不低于 300 元的男性有 20 人，低 于 300 元的男性有 25 人，根据统计数据完成下列 2 2 列联表，并判断是否有99%的把握认为消费 金额与性别有关？ （3）分析人员对抽取对象每周的消费金额 y 与年龄 x 进一步分析，发现他们线性相关，得到回归方 程 ˆ 5y x b   ．已知 100 名使用者的平均年龄为 38 岁，试判断一名年龄为 25 岁的年轻人每周的平 均消费金额为多少．（同一组数据用该区间的中点值代替） 2 2 列联表 男性 女性 合计 消费金额 300 消费金额 300 合计 临界值表： 2 0( )P K k 0．050 0．010 0．001 4 0k 3．841 6．635 10．828 2 2 ( ) ( )( )( )( ) n ad bcK a b c d a c b d      ，其中 n a b c d    ． 20．（12 分）如图，在三棱柱 1 1 1ABC A B C 中， 1CC  平面 1 1 1A B C ，D 为 1AB 的中点， 1B C 交 1BC 于点 E ， AC BC ， 2BC AC  ． （1）证明： DE 平面 1 1BB C C ； （2）若 1 1C B AB ，求二面角 1 1A B C A  的余弦值． 21．（12 分）设函数      1 ln 1f x mx x   ． （1）若当 0 1x  时，函数  f x 的图象恒在直线 y x 上方，求实数 m 的取值范围； （2）求证： 1000. 61001( )1000e  ． 5 22．（12 分）已知椭圆   2 2 2 2: 1 0x yC a b a b   的离心率为 3 2 ，过椭圆的焦点且与长轴垂直的 弦长为 1． （1）求椭圆C 的方程； （2）设点 M 为椭圆上位于第一象限内一动点， , A B 分别为椭圆的左顶点和下顶点，直线 MB 与 x 轴交于点C ，直线 MA 与轴交于点 D ，求证：四边形 ABCD 的面积为定值． （新高考）2021 届高三入学调研试卷 数 学（三）答 案 注意事项： 1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证 号条形码粘贴在答题卡上的指定位置。 2．选择题的作答：每小题选出答案后，用 2B 铅笔把答题卡上对应题目的答案标 号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。 3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。写在试题 卷、草稿纸和答题卡上的非答题区域均无效。 4．考试结束后，请将本试题卷和答题卡一并上交。 第Ⅰ卷 一、单项选择题：本题共 8 小题，每小题 5 分，共 40 分．在每小题给出的四个选项 中，只有一项是符合题目要求的． 1．【答案】C 【解析】由题意得，  4 2M x x    ，  2 3N x x    ， 则  2 2M N x x    ，故选 C． 2．【答案】D 【解析】由 2 1 i(1 i) z   ，得 2(1 i) 2i 2i(1 i) 1 i1 i 1 i (1 i)(1 i)z           ，故选 D． 3．【答案】B 【解析】当按照3:1:1进行分配时，则有 1 3 3 3C A 18 种不同的方案； 当按照 2: 2:1进行分配，则有 2 3 3 3C A 18 种不同的方案， 故共有 36 种不同的派遣方案，故选 B． 4．【答案】C 【解析】将正方形放入如图所示的平面直角坐标系中，设 0( ),E x ， 0 1x  ， 又 11, 2M      ，C(1，1)，所以 11 , 2EM x      ，  1 ,1EC x  ， 所以    21 11 , 1 ,1 12 2EC EM x x x             ， 因为 0 1x  ，所以  21 1 312 2 2x    ， 即 EC EM   的取值范围是 1 3,2 2      ，故选 C． 5．【答案】B 【解析】由条件得   2(3 9)f a f a   ，即 2 2 1 3 1 1 9 1 3 9 a a a a             ，∴ (2 2,3)a ， 故选 B． 6．【答案】D 【解析】因为 P ABCD- 的四条侧棱都相等，底面是边长为 2 的正方形， 则点 P 在面 ABCD 内的射影落在正方形 ABCD 的中心，连接 ,AC BD 交于点 E ， 设球心为O，连接 ,PO BO ，则 E 在直线 PO 上， PO BO R  ， 由 2 81π4π 4R  ，解得 9 4R  ， 又 22 BDBE   ，所以 2 2 81 7216 4OE R BE     ， 所以 9 7 1 4 4 2PE R OE     或 9 7 44 4PE R OE     ， 当 1 2PE  时， 2 2 1 324 2PA AE PE     ， 则 PA 与底面 ABCD 所成角的正弦值为 1 12 3 3 2 PE AP   ， 当 4PE  时， 2 2 16 2 3 2PA AE PE     ， 则 PA 与底面 ABCD 所成角的正弦值为 4 2 2 33 2 PE AP   ， 即 PA 与底面 ABCD 所成角的正弦值为 1 3 或 2 2 3 ，故选 D． 7．【答案】B 【解析】由题意，二项式 8ax x     的展开式中的通项公式   8 2 1 8C rr r rT a x     ， 令8 2 2r  ，解得 3r  ， 所以含 2x 项的系数为  33 8 7C a   ，解得 1 2a  ，故选 B． 8．【答案】B 【解析】由图知，当 0 2x  时，函数  y f x 取得最大值，此时   π40sin 133f x x     ； 当 2x  时，   0.590 14xf x e   ，当车辆驾驶人员血液中酒精小于 20mg /100 mL 时可以 开车，此时 2x  ． 由 0.590 14 20xe   ，得 0.5 1 15 xe  ，两边取自然对数得 10.5 ln15x  ， 即 0.5 ln15x   ，解得 ln15 2.71 5.420.5 0.5x    ， 所以，喝啤酒需6个小时候才可以合法驾车，故选 B． 二、多项选择题：本题共 4 小题，每小题 5 分，共 20 分．在每小题给出的选项中， 有多项符合题目要求．全部选对的得 5 分，部分选对的得 3 分，有选错的得 0 分． 9．【答案】CD 【解析】抛物线 2 12y x 的焦点  3,0F ，故 2 24 3b  ， 2 5b  ， 故双曲线方程为 2 2 14 5 x y  ，双曲线的实轴长为 2 4a  ，A 错误； 双曲线的离心率为 3 2 ce a   ，B 错误； 双曲线的渐近线方程为 5 2y x  ，C 正确； F 到渐近线的距离为 3 5 2 5 51 4 d    ，D 正确， 故选 CD． 10．【答案】BCD 【解析】由函数    sinf x A x   （其中 0A  ， 0 ，0 π  ）的图像可得 2A  ， 2π 5π π 4 3 12 4 T    ， 因此 πT  ， 2π 2π    ， 所以    2sin 2f x x   ，过点 2π , 23     ， 因此 4π 3π 2 π,3 2 k k   Z ， 又 0 π  ，所以 6 π ，   π2sin 2 6f x x      ， 当 π 2x  时， π 12f       ，故 A 错； 当 π 12x   时， π 012f      ，故 B 正确； 当 π π,3 6x      ， π π π2 ,2 26x       ，所以   π2sin 2 6f x x     在 π π,3 6x      上单调递 增，故 C 正确； 当 π 23π 12 12x   时，  π2 0,4π6x   ， 所 以 1y  与 函 数  y f x 有 4 的 交 点 的 横 坐 标 为 1 2 3 4, , ,x x x x ， 1 2 3 4 π 7π 8π2 26 6 3x x x x        ，故 D 正确， 故选 BCD． 11．【答案】ABD 【解析】对于 A，   2 22 2 2 2 1 1 11 2 22 1 2 2 2a b a a a a a              ， 当且仅当 1 2a b  时，等号成立，故 A 正确； 对于 B， 2 1 1a b a     ，所以 1 12 2 2 a b   ，故 B 正确； 对于 C， 2 2 2 2 2 2 1log log log log log 22 4 a ba b ab          ， 当且仅当 1 2a b  时，等号成立，故 C 不正确； 对于 D，因为 2 1 2 1 2a b ab a b       ， 所以 2a b  ，当且仅当 1 2a b  时，等号成立，故 D 正确， 故选 ABD． 12．【答案】AC 【解析】    2100 2001 10 2π x f x e   ，故 100  ， 2 100  ，故 A 正确，B 错误；      120 80 70p x p x p x     ，故 C 正确； 根据正态分布的对称性知：      100 110 90 100 80 90p x p x p x        ，故 D 错 误， 故选 AC． 第Ⅱ卷 三、填空题：本大题共 4 小题，每小题 5 分，共 20 分． 13．【答案】 3 4 【解析】过 F 且斜率为 3 的直线方程为 3( 1)y x  ， 与抛物线 2: 4C y x 联立得 2 10 3 0x x   ． (3,2 3)A ， 1 2 3,3 3B      ， 则直线 AO 方程为 2 3 3y x ，与 : 1l x   的交点 2 31, 3D       ， 因此 | | 1 3 4| | 4 3 OF BD   ，故答案为 3 4 ． 14．【答案】 1 e 【解析】由题意   ln , 1 ( ) ln ln , 0 1 x x x f x x x x xx       ， 因为 1x  时， 1 1 1 ln( ) ( ) ln 0xf x f x xx x      ； 1x  时， 1 ln 1 1( ) ( ) ln 0xf x f x x x x     ， 所以 0x  时， 1( ) ( ) 0f x f x   恒成立， 因为正项数列 na 是公比大于 0 的等比数列，且 1010 1a  ， 所以 2 1 2019 2 2018 1009 1011 1010 1a a a a a a a     ， 所以            1 2019 2012 1009 108 11 0f a f a f a f a f a f a       ， 又 1010( ) 0f a  ，          1 2 3 2019 2020f a f a f a f a f a e       ， 所以 2020( )f a e  ， 当 1q  时， 2020 1a  ，所以 2020 2020lna a e  ，此时无解； 当 1q  时， 20200 1a  ，所以 2020 2020 ln a ea   ，解得 2020 1a e  ， 故答案为 1 e ． 15．【答案】2 【解析】因为球的直径 4DC  ，且 π 6ADC BDC    ， 所以 2AC BC  ， 2 3AD BD  ， 1 3A BCD BCDV S h   △ （其中 h 为点 A 到底面 BCD的距离）， 故当 h 最大时， A BCDV  的体积最大， 即当面 ADC  面 BDC 时， h 最大且满足 4 2 2 3h   ， 即 3h  ，此时 1 1 2 2 3 3 23 2A BCDV        ． 16．【答案】 π(0,2 ]2  【解析】由题意得C 在线段 AB 中垂线上，所以C 到直线l 上的距离取值范围为 (0,1]， 因 此 圆 弧 AC ， 圆 弧 CB 与 线 段 AB 围 成 图 形 面 积 S 的 取 值 范 围 是 2 2π π(0,2(1 1 )] (0,2 ]4 2     ， 故答案为 π(0,2 ]2  ． 四、解答题：本大题共 6 个大题，共 70 分．解答应写出文字说明、证明过程或演算 步骤． 17．【答案】（1） 1 2 ；（2） 13b  ． 【解析】（1）由 ABC△ 的面积为 2 2sin AD B 且 D 为 BC 的中点可知： ABD△ 的面积为 2 4sin AD B ， 由三角形的面积公式可知 21 sin2 4sin ADAB BD B B    ， 由正弦定理可得 2sin sin 1BAD BDA    ，所以 1sin sin 2BAD BDA    ． （2）因为 2BD AB ，所以在 ABD△ 中，由正弦定理可得 sin sin BD AB BAD BDA   ， 所以 sin 2sinBAD BDA   ， 由（1）可知 1sin sin 2BAD BDA    ，所以sin 1BAD  ， 1sin 2BDA  ， ∵ (0,π)BAD  ，∴ π 2BAD  ， 在直角 ABD△ 中， 3AD  ， 1sin 2BDA  ，所以 2BD  ， 1AB  ， ∵ 2BC BD ， 4BC  ， 在 ABC△ 中用余弦定理，可得 2 2 2 12 cos 1 16 2 1 4 132b a c ac B          ， 13b  ． 18．【答案】（1）②，理由见解析；（2） 2 1n nT n   ． 【解析】（1）①③不能使 na 成等比数列，②可以． 由题意   4 ( 1) 2 2 2nf a n n      ， 即 log 2 2k na n  ，得 2 2n na k  ，且 4 1 0a k  ， 2( 1) 2 21 2 2 n n n n a k ka k       ． 常数 0k  且 1k  ， 2k 为非零常数， 数列 na 是以 4k 为首项， 2k 为公比的等比数列． （2）由（1）知   14 2 2 2n k na k k k     ，所以当 2k  时， 12n na  ， 因为 1 2 2 4 1    n n na b n ，所以 2 1 4 1nb n   ， 所以 1 1 1 1 (2 1)(2 1) 2 2 1 2 1nb n n n n          ， 1 2 1 1 1 1 1 11 L2 3 3 5 1 112 2 1 22 1 2 1 1n nT b b nb n nn n                       ． 19．【答案】（1） 0.0035m  ， 0.0025n  ；（2）列联表见解析，有 99%的把握认为；（3） 395 元． 【解析】（1）由频率分布直方图可知， 0.01 0.0015 2 0.001 0.006m n      ， 由中间三组的人数成等差数列可知 0.0015 2m n  ， 可解得 0.0035m  ， 0.0025n  ． （2）周平均消费不低于 300 元的频率为 0.0035 0.0015 0.001 100 0.6    ， 因此 100 人中，周平均消费不低于 300 元的人数为100 0.6 60  人． 所以 2 2 列联表为 男性 女性 合计 消费金额 300 20 40 60 消费金额 300 25 15 40 合计 45 55 100 2 2 100(20 15 25 40) 8.249 6.63545 55 60 40K        ， 所以有99% 的把握认为消费金额与性别有关． （3）调查对象的周平均消费为 2( ) 2 4f x kx x k   ， 由题意330 5 38 b    ，∴ 520b  ， 5 25 520 395y      ． ∴该名年龄为 25 岁的年轻人每周的平均消费金额为 395 元． 20．【答案】（1）证明见解析；（2） 6 3 ． 【解析】证明：（1）因为 1 1 1ABC A B C 为三棱柱，所以平面 1 1 1A B C ∥平面 ABC ， 因为 1CC  平面 1 1 1A B C ，所以 1CC  平面 ABC ． 又因为 AC  平面 ABC ，所以 1AC CC ． 又因为 AC BC ， 1CC BC C ， 1CC BC 、 平面 1 1BB C C ， 所以 AC  平面 1 1BB C C ． 由题知：四边形 1 1BB C C 为矩形，又因 1B C 交 1BC 于点 E ，所以 E 为 1B C 的中点， 又因为 D 为 1AB 的中点，所以 DE 为 1AB CV 的中位线，所以 DE AC∥ ， 所以 DE 平面 1 1BB C C ． （2）由（1）知： 1 1 1 1 1C A C B C C、 、 两两互相垂直，所以以 1C 为坐标原点，分别以 1 1 1 1 1C A C B C C、 、 为 x y z、 、 轴建立空间直角坐标系 1C xyz ，如图所示： 设 1 ( 0)CC h h  ， 则 1(0,0,0)C ， 1(2,0,0)A ， 1(0,2,0)B ，  2,0,A h ， (0,2, )B h ， (0,0, )C h ， 所以 1 (0,2, )C B h ， 1 ( 2,2, )AB h   ， 因为 1 1C B AB ，所以 1 1 0C B AB   ，所以    0 2 2 2 0h h        ，解得 2h  ， 所以  2,0,2A ， (0,2,2)B ， (0,0,2)C ， 所以 1 ( 2,2, 2)AB    ， ( 2,0,0)AC   ， 1 1 ( 2,2,0)A B   ， 1 ( 2,0,2)AC   ， 设平面 1AB C 的法向量为 ( , , )x y zn ，则 1 0 0 AB AC        n n ，所以 2 2 2 0 2 0 x y z x       ， 不妨令 1y  ，则  0,1,1n ； 设平面 1 1A B C 的法向量为 ( , , )x y zm ，则 1 1 1 0 0 A B AC        m m ，所以 2 2 0 2 2 0 x y x z       ， 不妨令 1y  ，则  1,1,1m ， 所以 2 6cos 32 3      m nm n m n ， 因为平面 1 1A B C 与平面 1AB C 所成的角为锐角， 所以二面角 1 1A B C A  的余弦值为 6 3 ． 21．【答案】（1） 1, 2      ；（2）证明见解析． 【解析】（1）由题知当 (0,1)x 时，不等式(1 )ln(1 )mx x x   恒成立， 因为 ln(1 ) 0x  ，故必有1 0mx  在 (0,1)x 上恒成立． 此时，该不等式等价于 ln(1 ) 1 xx mx    ， 令 ( ) ln(1 ) 1 xg x x mx     ，则 2 2 2 2 1 1 (2 1)( ) 1 (1 ) (1 )(1 ) m x m xg x x mx x mx         ， 故 ( )g x 与 2 (2 1)m x m  同号． 因 (0) 0g  ， 当 2 1 0m   时， ( )g x 在 2 2 1(0, )m m  递减，显然不符合 ( ) (0) 0g x g  ， 故必 2 1 0m   ； 当 2 1 0m   时，即 1 2m   时， ( ) 0g x  在 (0,1) 上恒成立， 即 ( )g x 在 (0,1) 递增，满足 ( ) (0) 0g x g  ， 故 1 2m   ． （2） 1000. 61001( )1000e  等价于不等式 31000 51(1 )1000 e    ， 两边取对数得 3 1(1000 )ln(1 ) 15 1000    ， 即证明 3 1 1 1(1 )ln(1 )5 1000 1000 1000     恒成立． 由（1）知当 (0,1)x ， 1( , )2m   时有 (1 )ln(1 )mx x x   恒成立． 故令 3 5m   ， 1 1000x  ， 即得 3 1 1 1(1 )ln(1 )5 1000 1000 1000     恒成立， 即 1000. 61001( )1000e  成立． 22．【答案】（1） 2 2 14 x y  ；（2）证明见解析． 【解析】（1）由已知可得 2 2 2 2 3 2 2 1 c a b a a b c           ，解得 2 1 a b    ， 所以椭圆 C 的方程为 2 2 14 x y  ． （2）因为椭圆 C 的方程为 2 2 14 x y  ，所以  2,0A  ，  0, 1B  ， 设   , 0, 0M m n m n  ，则 2 2 14 m n  ，即 2 24 4m n  ． 则直线 BM 的方程为 1 1ny xm   ，令 0y  ，得 1C mx n   ； 同理：直线 AM 的方程为  22 ny xm   ，令 0x  ，得 2 2D ny m   ， 所以      22 21 1 2 12 12 2 1 2 2 2 1ABCD m nm nS AC BD n m m n               2 21 4 4 4 4 8 1 4 4 8 8 22 2 2 2 2 2 m n mn m n mn m n mn m n mn m n                  ， 即四边形 ABCD 的面积为定值 2．