2012年福建省高考数学试卷（文科） 22页

‎2012年福建省高考数学试卷（文科）‎ ‎　‎ 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．（5分）复数（2+i）2等于（　　）‎ A．3+4i B．5+4i C．3+2i D．5+2i ‎2．（5分）已知集合M={1，2，3，4}，N={﹣2，2}，下列结论成立的是（　　）‎ A．N⊆M B．M∪N=M C．M∩N=N D．M∩N={2}‎ ‎3．（5分）已知向量=（x﹣1，2），=（2，1），则⊥的充要条件是（　　）‎ A．x=﹣ B．x=﹣1 C．x=5 D．x=0‎ ‎4．（5分）一个几何体的三视图形状都相同，大小均相等，那么这个几何体不可以是（　　）‎ A．球 B．三棱锥 C．正方体 D．圆柱 ‎5．（5分）已知双曲线﹣=1的右焦点为（3，0），则该双曲线的离心率等于（　　）‎ A． B． C． D．‎ ‎6．（5分）阅读如图所示的程序框图，运行相应的程序，输出s值等于（　　）‎ A．﹣3 B．﹣10 C．0 D．﹣2‎ ‎7．（5分）直线x+﹣2=0与圆x2+y2=4相交于A，B两点，则弦AB的长度等于（　　）‎ A．2 B．2 C． D．1‎ ‎8．（5分）函数f（x）=sin（x﹣）的图象的一条对称轴是（　　）‎ A．x= B．x= C．x=﹣ D．x=﹣‎ ‎9．（5分）设f（x）=，g（x）=，则f（g（π））的值为（　　）‎ A．1 B．0 C．﹣1 D．π ‎10．（5分）若直线y=2x上存在点（x，y）满足约束条件，则实数m的最大值为（　　）‎ A．﹣1 B．1 C． D．2‎ ‎11．（5分）数列{an}的通项公式an=ncos，其前n项和为Sn，则S2012等于（　　）‎ A．1006 B．2012 C．503 D．0‎ ‎12．（5分）已知f（x）=x3﹣6x2+9x﹣abc，a＜b＜c，且f（a）=f（b）=f（c）=0．现给出如下结论：‎ ‎①f（0）f（1）＞0；‎ ‎②f（0）f（1）＜0；‎ ‎③f（0）f（3）＞0；‎ ‎④f（0）f（3）＜0．‎ 其中正确结论的序号是（　　）‎ A．①③ B．①④ C．②③ D．②④‎ ‎　‎ 二、填空题：本大题共4小题，每小题4分，共16分．把答案填在答题卡的相应位置．‎ ‎13．（4分）在△ABC中，已知∠BAC=60°，∠ABC=45°，BC=，则AC=　　．‎ ‎14．（4分）一支田径队有男女运动员98人，其中男运动员有56人．按男女比例用分层抽样的方法，从全体运动员中抽出一个容量为28的样本，那么应抽取女运动员人数是　　．‎ ‎15．（4分）已知关于x的不等式x2﹣ax+2a＞0在R上恒成立，则实数a的取值范围是　　．‎ ‎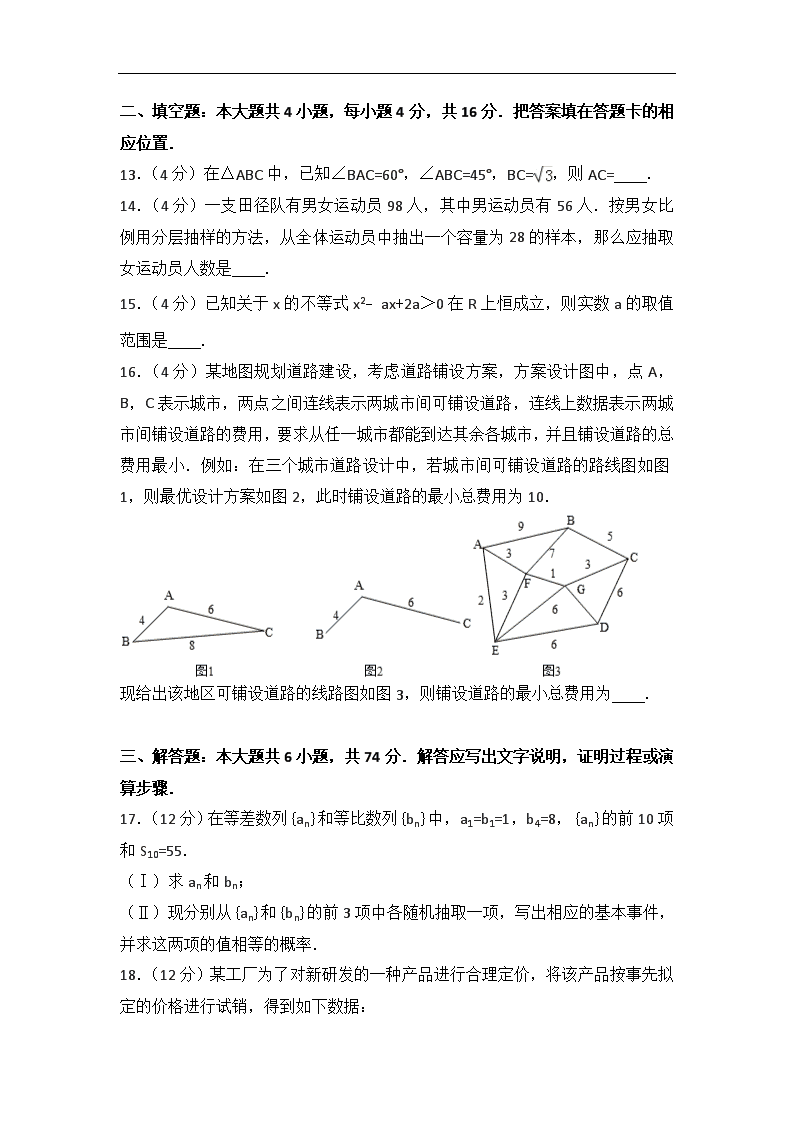16．（4分）某地图规划道路建设，考虑道路铺设方案，方案设计图中，点A，B，C表示城市，两点之间连线表示两城市间可铺设道路，连线上数据表示两城市间铺设道路的费用，要求从任一城市都能到达其余各城市，并且铺设道路的总费用最小．例如：在三个城市道路设计中，若城市间可铺设道路的路线图如图1，则最优设计方案如图2，此时铺设道路的最小总费用为10．‎ 现给出该地区可铺设道路的线路图如图3，则铺设道路的最小总费用为　　．‎ ‎　‎ 三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．‎ ‎17．（12分）在等差数列{an}和等比数列{bn}中，a1=b1=1，b4=8，{an}的前10项和S10=55．‎ ‎（Ⅰ）求an和bn；‎ ‎（Ⅱ）现分别从{an}和{bn}的前3项中各随机抽取一项，写出相应的基本事件，并求这两项的值相等的概率．‎ ‎18．（12分）某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：‎ 单价x（元）‎ ‎8‎ ‎8.2‎ ‎8.4‎ ‎8.6‎ ‎8.8‎ ‎9‎ 销量y（件）‎ ‎90‎ ‎84‎ ‎83‎ ‎80‎ ‎75‎ ‎68‎ ‎（Ⅰ）求回归直线方程=bx+a，其中b=﹣20，a=﹣b；‎ ‎（Ⅱ）预计在今后的销售中，销量与单价仍然服从（I）中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？（利润=销售收入﹣成本）‎ ‎19．（12分）如图，在长方体ABCD﹣A1B1C1D1中，AB=AD=1，AA1=2，M为棱DD1上的一点．‎ ‎（1）求三棱锥A﹣MCC1的体积；‎ ‎（2）当A1M+MC取得最小值时，求证：B1M⊥平面MAC．‎ ‎20．（12分）某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数．‎ ‎（1）sin213°+cos217°﹣sin13°cos17°‎ ‎（2）sin215°+cos215°﹣sin15°cos15°‎ ‎（3）sin218°+cos212°﹣sin18°cos12°‎ ‎（4）sin2（﹣18°）+cos248°﹣sin2（﹣18°）cos48°‎ ‎（5）sin2（﹣25°）+cos255°﹣sin2（﹣25°）cos55°‎ ‎（Ⅰ）试从上述五个式子中选择一个，求出这个常数；‎ ‎（Ⅱ）根据（Ⅰ）的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论．‎ ‎21．（12分）如图，等边三角形OAB的边长为 ‎，且其三个顶点均在抛物线E：x2=2py（p＞0）上．‎ ‎（1）求抛物线E的方程；‎ ‎（2）设动直线l与抛物线E相切于点P，与直线y=﹣1相较于点Q．证明以PQ为直径的圆恒过y轴上某定点．‎ ‎22．（14分）已知函数f（x）=axsinx﹣（a∈R），且在上的最大值为，‎ ‎（1）求函数f（x）的解析式；‎ ‎（2）判断函数f（x）在（0，π）内的零点个数，并加以证明．‎ ‎　‎ ‎2012年福建省高考数学试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．（5分）（2012•福建）复数（2+i）2等于（　　）‎ A．3+4i B．5+4i C．3+2i D．5+2i ‎【分析】直接根据复数的乘法的运算法则，以及i2=﹣1可求出所求．‎ ‎【解答】解：（2+i）2=4+4i+i2=3+4i 故选A．‎ ‎　‎ ‎2．（5分）（2012•福建）已知集合M={1，2，3，4}，N={﹣2，2}，下列结论成立的是（　　）‎ A．N⊆M B．M∪N=M C．M∩N=N D．M∩N={2}‎ ‎【分析】由M={1，2，3，4}，N={﹣2，2}，则可知，﹣2∈N，但是﹣2∉M，则N⊄M，M∪N={1，2，3，4，﹣2}≠M，M∩N={2}≠N，从而可判断．‎ ‎【解答】解：A、由M={1，2，3，4}，N={﹣2，2}，可知﹣2∈N，但是﹣2∉M，则N⊄M，故A错误；‎ B、M∪N={1，2，3，4，﹣2}≠M，故B错误；‎ C、M∩N={2}≠N，故C错误；‎ D、M∩N={2}，故D正确．‎ 故选D．‎ ‎　‎ ‎3．（5分）（2012•福建）已知向量=（x﹣1，2），=（2，1），则⊥的充要条件是（　　）‎ A．x=﹣ B．x=﹣1 C．x=5 D．x=0‎ ‎【分析】直接利用向量垂直的充要条件，通过坐标运算求出x的值即可．‎ ‎【解答】解：因为向量=（x﹣1，2），=（2，1），⊥，‎ 所以2（x﹣1）+2=0，解得x=0．‎ 故选D．‎ ‎　‎ ‎4．（5分）（2012•福建）一个几何体的三视图形状都相同，大小均相等，那么这个几何体不可以是（　　）‎ A．球 B．三棱锥 C．正方体 D．圆柱 ‎【分析】利用简单几何体的结构特征以及三视图的定义，容易判断圆柱的三视图不可能形状相同，大小均等 ‎【解答】解：A、球的三视图均为圆，且大小均等；‎ B、三条侧棱两两垂直且相等的适当高度的正三棱锥，其一个侧面放到平面上，其三视图均为三角形且形状都相同；‎ C、正方体的三视图可以是三个大小均等的正方形；‎ D、圆柱的三视图中必有一个为圆，其他两个为矩形．‎ 故一个几何体的三视图形状都相同，大小均等，那么这个几何体不可以是圆柱．‎ 故选D．‎ ‎　‎ ‎5．（5分）（2012•福建）已知双曲线﹣=1的右焦点为（3，0），则该双曲线的离心率等于（　　）‎ A． B． C． D．‎ ‎【分析】根据双曲线﹣=1的右焦点为（3，0），可得a=2，进而可求双曲线的离心率．‎ ‎【解答】解：∵双曲线﹣=1的右焦点为（3，0），‎ ‎∴a2+5=9‎ ‎∴a2=4‎ ‎∴a=2‎ ‎∵c=3‎ ‎∴‎ 故选C．‎ ‎　‎ ‎6．（5分）（2012•福建）阅读如图所示的程序框图，运行相应的程序，输出s值等于（　　）‎ A．﹣3 B．﹣10 C．0 D．﹣2‎ ‎【分析】通过循环，计算s，k的值，当k=4时退出循环，输出结果即可．‎ ‎【解答】解：k=1，满足判断框，第1次循环，s=1，k=2，‎ 第2次判断后循环，s=0，k=3，‎ 第3次判断并循环s=﹣3，k=4，第3次判断退出循环，‎ 输出S=﹣3．‎ 故选：A．‎ ‎　‎ ‎7．（5分）（2012•福建）直线x+﹣2=0与圆x2+y2=4相交于A，B两点，则弦AB的长度等于（　　）‎ A．2 B．2 C． D．1‎ ‎【分析】由直线与圆相交的性质可知，，要求AB，只要先求圆心（0，0）到直线x+﹣2=0的距离d，即可求解 ‎【解答】解：∵圆心（0，0）到直线x+﹣2=0的距离d=‎ 由直线与圆相交的性质可知，‎ 即 ‎∴‎ 故选B ‎　‎ ‎8．（5分）（2012•福建）函数f（x）=sin（x﹣）的图象的一条对称轴是（　　）‎ A．x= B．x= C．x=﹣ D．x=﹣‎ ‎【分析】将内层函数x﹣看做整体，利用正弦函数的对称轴方程，即可解得函数f（x）的对称轴方程，对照选项即可得结果 ‎【解答】解：由题意，令x﹣=kπ+，k∈z 得x=kπ+，k∈z是函数f（x）=sin（x﹣）的图象对称轴方程 令k=﹣1，得x=﹣‎ 故选 C ‎　‎ ‎9．（5分）（2012•福建）设f（x）=，g（x）=，则f（g（π））的值为（　　）‎ A．1 B．0 C．﹣1 D．π ‎【分析】根据π是无理数可求出g（π）的值，然后根据分段函数f（x）的解析式可求出f（g（π））的值．‎ ‎【解答】解：∵π是无理数 ‎∴g（π）=0‎ 则f（g（π））=f（0）=0‎ 故选B．‎ ‎　‎ ‎10．（5分）（2012•福建）若直线y=2x上存在点（x，y）满足约束条件，则实数m的最大值为（　　）‎ A．﹣1 B．1 C． D．2‎ ‎【分析】根据，确定交点坐标为（1，2）要使直线y=2x上存在点（x，y）满足约束条件，则m≤1，由此可得结论．‎ ‎【解答】解：由题意，，可求得交点坐标为（1，2）‎ 要使直线y=2x上存在点（x，y）满足约束条件，如图所示．可得m≤1‎ ‎∴实数m的最大值为1‎ 故选B．‎ ‎　‎ ‎11．（5分）（2012•福建）数列{an}的通项公式an=ncos，其前n项和为Sn，则S2012等于（　　）‎ A．1006 B．2012 C．503 D．0‎ ‎【分析】由已知得f（n）=cos是以T==4为周期的周期函数，由此能求出S2012的值．‎ ‎【解答】解：∵an=ncos，‎ 又∵f（n）=cos是以T==4为周期的周期函数，‎ ‎∴a1+a2+a3+a4=（0﹣2+0+4）=2，a5+a6+a7+a8=（0﹣6+0+8）=2，‎ ‎…‎ a2009+a2010+a2011+a2012=（0﹣2010+0+2012）=2，‎ S2012=a1+a2+a3+a4+…+a2012‎ ‎=（0﹣2+0+4）+（0﹣6+0+8）+…+（0﹣2010+0+2012）‎ ‎=2×503=1006‎ 故选：A．‎ ‎　‎ ‎12．（5分）（2012•福建）已知f（x）=x3﹣6x2+9x﹣abc，a＜b＜c，且f（a）=f（b）=f（c）=0．现给出如下结论：‎ ‎①f（0）f（1）＞0；‎ ‎②f（0）f（1）＜0；‎ ‎③f（0）f（3）＞0；‎ ‎④f（0）f（3）＜0．‎ 其中正确结论的序号是（　　）‎ A．①③ B．①④ C．②③ D．②④‎ ‎【分析】根据f（x）=x3﹣6x2+9x﹣abc，a＜b＜c，且f（a）=f（b）=f（c）=0，确定函数的极值点及a、b、c的大小关系，由此可得结论．‎ ‎【解答】解：求导函数可得f′（x）=3x2﹣12x+9=3（x﹣1）（x﹣3），‎ ‎∵a＜b＜c，且f（a）=f（b）=f（c）=0．‎ ‎∴a＜1＜b＜3＜c，‎ 设f（x）=（x﹣a）（x﹣b）（x﹣c）=x3﹣（a+b+c）x2+（ab+ac+bc）x﹣abc，‎ ‎∵f（x）=x3﹣6x2+9x﹣abc，‎ ‎∴a+b+c=6，ab+ac+bc=9，‎ ‎∴b+c=6﹣a，‎ ‎∴bc=9﹣a（6﹣a）＜，‎ ‎∴a2﹣4a＜0，‎ ‎∴0＜a＜4，‎ ‎∴0＜a＜1＜b＜3＜c，‎ ‎∴f（0）＜0，f（1）＞0，f（3）＜0，‎ ‎∴f（0）f（1）＜0，f（0）f（3）＞0．‎ 故选：C．‎ ‎　‎ 二、填空题：本大题共4小题，每小题4分，共16分．把答案填在答题卡的相应位置．‎ ‎13．（4分）（2012•福建）在△ABC中，已知∠BAC=60°，∠ABC=45°，BC=‎ ‎，则AC=　　．‎ ‎【分析】结合已知两角一对边，要求B的对边，可利用正弦定理，进行求解 ‎【解答】解：∵∠BAC=60°，∠ABC=45°，‎ ‎∴BC=‎ 由正弦定理可得，可得AC===‎ 故答案为：‎ ‎　‎ ‎14．（4分）（2012•福建）一支田径队有男女运动员98人，其中男运动员有56人．按男女比例用分层抽样的方法，从全体运动员中抽出一个容量为28的样本，那么应抽取女运动员人数是　12　．‎ ‎【分析】根据田径队的男女运动员数目和用分层抽样要抽取的数目，得到每个个体被抽到的概率，利用每个个体被抽到的概率乘以女运动员的数目，得到结果．‎ ‎【解答】解：∵田径队有男女运动员98人，其中男运动员有56人，‎ ‎∴这支田径队有女运动员98﹣56=42人，‎ 用分层抽样的方法从该队的全体运动员中抽取一个容量为28的样本，‎ ‎∴每个个体被抽到的概率是=‎ ‎∵田径队有女运动员42人，‎ ‎∴女运动员要抽取42×=12人，‎ 故答案为：12‎ ‎　‎ ‎15．（4分）（2012•福建）已知关于x的不等式x2﹣ax+2a＞0在R上恒成立，则实数a的取值范围是　（0，8）　．‎ ‎【分析】将关于x的不等式x2﹣ax+2a＞0在R上恒成立，转化成△＜0，从而得到关于a的不等式，求得a的范围．‎ ‎【解答】解：因为不等式x2﹣ax+2a＞0在R上恒成立．‎ ‎∴△=（﹣a）2﹣8a＜0，解得0＜a＜8‎ 故答案为：（0，8）．‎ ‎　‎ ‎16．（4分）（2012•福建）某地图规划道路建设，考虑道路铺设方案，方案设计图中，点A，B，C表示城市，两点之间连线表示两城市间可铺设道路，连线上数据表示两城市间铺设道路的费用，要求从任一城市都能到达其余各城市，并且铺设道路的总费用最小．例如：在三个城市道路设计中，若城市间可铺设道路的路线图如图1，则最优设计方案如图2，此时铺设道路的最小总费用为10．‎ 现给出该地区可铺设道路的线路图如图3，则铺设道路的最小总费用为　16　．‎ ‎【分析】确定铺设道路的总费用最小时的线路为：A→E→F→G→D，从G分叉，G→C→B，即可求得铺设道路的最小总费用．‎ ‎【解答】解：由题意，铺设道路的总费用最小时的线路为：A→E→F→G→D，从G分叉，G→C→B 总费用为2+3+1+2+3+5=16‎ 故答案为：16‎ ‎　‎ 三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．‎ ‎17．（12分）（2012•福建）在等差数列{an}和等比数列{bn}中，a1=b1=1，b4=8，{an}的前10项和S10=55．‎ ‎（Ⅰ）求an和bn；‎ ‎（Ⅱ）现分别从{an}和{bn}的前3项中各随机抽取一项，写出相应的基本事件，并求这两项的值相等的概率．‎ ‎【分析】（Ⅰ）先根据条件求出公差和公比，即可求出通项；‎ ‎（Ⅱ）先根据第一问的结果把基本事件都写出来，再找到满足要求的即可求出结论．‎ ‎【解答】解：（Ⅰ）设等差数列的公差为d，等比数列的公比为q．‎ 由题得：S10=10+d=55；b4=q3=8；‎ 解得：d=1，q=2．‎ 所以：an=n，bn=2n﹣1．．‎ ‎（Ⅱ）分别从从{an}和{bn}的前3项中各随机抽取一项，得到的基本事件有9个：‎ ‎（1，1），（1，2），（1，4），（2，1），（2，2），（2，4），（3，1），（3，2），（3，4）．‎ 两项的值相等的有（1，1），（2，2）．‎ ‎∴这两项的值相等的概率：．‎ ‎　‎ ‎18．（12分）（2012•福建）某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：‎ 单价x（元）‎ ‎8‎ ‎8.2‎ ‎8.4‎ ‎8.6‎ ‎8.8‎ ‎9‎ 销量y（件）‎ ‎90‎ ‎84‎ ‎83‎ ‎80‎ ‎75‎ ‎68‎ ‎（Ⅰ）求回归直线方程=bx+a，其中b=﹣20，a=﹣b；‎ ‎（Ⅱ）预计在今后的销售中，销量与单价仍然服从（I）中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？（利润=销售收入﹣成本）‎ ‎【分析】（I）计算平均数，利用b=﹣20，a=﹣b，即可求得回归直线方程；‎ ‎（II）设工厂获得的利润为L元，利用利润=销售收入﹣成本，建立函数，利用配方法可求工厂获得的利润最大．‎ ‎【解答】解：（I），=‎ ‎∵b=﹣20，a=﹣b，‎ ‎∴a=80+20×8.5=250‎ ‎∴回归直线方程=﹣20x+250；‎ ‎（II）设工厂获得的利润为L元，则L=x（﹣20x+250）﹣4（﹣20x+250）=﹣20‎ ‎∴该产品的单价应定为元，工厂获得的利润最大．‎ ‎　‎ ‎19．（12分）（2012•福建）如图，在长方体ABCD﹣A1B1C1D1中，AB=AD=1，AA1=2，M为棱DD1上的一点．‎ ‎（1）求三棱锥A﹣MCC1的体积；‎ ‎（2）当A1M+MC取得最小值时，求证：B1M⊥平面MAC．‎ ‎【分析】（1）由题意可知，A到平面CDD1C1的距离等于AD=1，易求=1，从而可求；‎ ‎（2）将侧面CDD1C1绕DD1逆时针转90°展开，与侧面ADD1A1共面，当A1，M，C′共线时，A1M+MC取得最小值．易证CM⊥平面B1C1M，从而CM⊥B1M，同理可证，B1M⊥AM，‎ 问题得到解决．‎ ‎【解答】解：（1）由长方体ABCD﹣A1B1C1D1知，AD⊥平面CDD1C1，‎ ‎∴点A到平面CDD1C1的距离等于AD=1，‎ 又=CC1×CD=×2×1=1，‎ ‎∴=AD•=．‎ ‎（2）将侧面CDD1C1绕DD1逆时针转90°展开，与侧面ADD1A1共面，‎ 当A1，M，C′共线时，A1M+MC取得最小值．‎ 由AD=CD=1，AA1=2，得M为DD1的中点．连接C1M，在△C1MC中，C1M=，MC=，C1C=2，‎ ‎∴=+MC2，得∠CMC1=90°，即CM⊥C1M，又B1C1⊥平面CDD1C1，‎ ‎∴B1C1⊥CM，又B1C1∩C1M=C1，‎ ‎∴CM⊥平面B1C1M，‎ ‎∴CM⊥B1M，同理可证，B1M⊥AM，又AM∩MC=M，‎ ‎∴B1M⊥平面MAC ‎　‎ ‎20．（12分）（2012•福建）某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数．‎ ‎（1）sin213°+cos217°﹣sin13°cos17°‎ ‎（2）sin215°+cos215°﹣sin15°cos15°‎ ‎（3）sin218°+cos212°﹣sin18°cos12°‎ ‎（4）sin2（﹣18°）+cos248°﹣sin2（﹣18°）cos48°‎ ‎（5）sin2（﹣25°）+cos255°﹣sin2（﹣25°）cos55°‎ ‎（Ⅰ）试从上述五个式子中选择一个，求出这个常数；‎ ‎（Ⅱ）根据（Ⅰ）的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论．‎ ‎【分析】（Ⅰ）选择（2），由sin215°+cos215°﹣sin15°cos15°=1﹣sin30°=，可得这个常数的值．‎ ‎（Ⅱ）推广，得到三角恒等式sin2α+cos2（30°﹣α）﹣sinαcos（30°﹣α）=．证明方法一：直接利用两角差的余弦公式代入等式的左边，化简可得结果．‎ 证明方法二：利用半角公式及两角差的余弦公式把要求的式子化为 +﹣sinα（cos30°cosα+sin30°sinα），即 1﹣+cos2α+sin2α ‎﹣sin2α﹣，化简可得结果．‎ ‎【解答】解：选择（2），计算如下：‎ sin215°+cos215°﹣sin15°cos15°=1﹣sin30°=，故 这个常数为．‎ ‎（Ⅱ）根据（Ⅰ）的计算结果，将该同学的发现推广，得到三角恒等式sin2α+cos2（30°﹣α）﹣sinαcos（30°﹣α）=．‎ 证明：（方法一）sin2α+cos2（30°﹣α）﹣sinαcos（30°﹣α）=sin2α+﹣sinα（cos30°cosα+sin30°sinα）‎ ‎=sin2α+cos2α+sin2α+sinαcosα﹣sinαcosα﹣sin2α=sin2α+cos2α=．‎ ‎（方法二）sin2α+cos2（30°﹣α）﹣sinαcos（30°﹣α）=+﹣sinα（cos30°cosα+sin30°sinα）‎ ‎=1﹣+（cos60°cos2α+sin60°sin2α）﹣sin2α﹣sin2α ‎=1﹣+cos2α+sin2α﹣sin2α﹣=1﹣﹣+‎ ‎=．‎ ‎　‎ ‎21．（12分）（2012•福建）如图，等边三角形OAB的边长为，且其三个顶点均在抛物线E：x2=2py（p＞0）上．‎ ‎（1）求抛物线E的方程；‎ ‎（2）设动直线l与抛物线E相切于点P，与直线y=﹣1相较于点Q．证明以PQ为直径的圆恒过y轴上某定点．‎ ‎【分析】（1）依题意，|OB|=8，∠BOy=30°，从而可得B（4，12），利用B在x2=2py（p＞0）上，可求抛物线E的方程；‎ ‎（2）由（1）知，，，设P（x0，y0），可得l：，与y=﹣1联立，求得取x0=2，x0=1，猜想满足条件的点M存在，再进行证明即可．‎ ‎【解答】解：（1）依题意，|OB|=8，∠BOy=30°，‎ 设B（x，y），则x=|OB|sin30°=4，y=|OB|cos30°=12‎ ‎∵B（4，12）在x2=2py（p＞0）上，∴‎ ‎∴p=2，‎ ‎∴抛物线E的方程为x2=4y；‎ ‎（2）由（1）知，，‎ 设P（x0，y0），则x0≠0．l：即 由得，∴‎ 取x0=2，此时P（2，1），Q（0，﹣1），以PQ为直径的圆为（x﹣1）2+y2‎ ‎=2，交y轴于点M1（0，1）或M2（0，﹣1）‎ 取x0=1，此时P（1，），Q（﹣，﹣1），以PQ为直径的圆为（x+）2+（y+）2=2，交y轴于点M3（0，1）或M4（0，﹣）‎ 故若满足条件的点M存在，只能是M（0，1），证明如下 ‎∵‎ ‎∴=2y0﹣2﹣2y0+2=0‎ 故以PQ为直径的圆恒过y轴上的定点M（0，1）．‎ ‎　‎ ‎22．（14分）（2012•福建）已知函数f（x）=axsinx﹣（a∈R），且在上的最大值为，‎ ‎（1）求函数f（x）的解析式；‎ ‎（2）判断函数f（x）在（0，π）内的零点个数，并加以证明．‎ ‎【分析】（I）由题意，可借助导数研究函数，在上的单调性，确定出最值，令最值等于，即可得到关于a的方程，由于a的符号对函数的最值有影响，故可以对a的取值范围进行讨论，分类求解；‎ ‎（II）借助导数研究函数f（x）在（0，π）内单调性，由零点判定定理即可得出零点的个数．‎ ‎【解答】解：（I）由已知得f′（x）=a（sinx+xcosx），对于任意的x∈（0，），有sinx+xcosx＞0，当a=0时，f（x）=﹣，不合题意；‎ 当a＜0时，x∈（0，），f′（x）＜0，从而f（x）在（0，）单调递减，‎ 又函数在上图象是连续不断的，故函数在上上的最大值为f（0）=﹣，不合题意；‎ 当a＞0时，x∈（0，），f′（x）＞0，从而f（x）在（0，）单调递增，‎ 又函数在上图象是连续不断的，故函数在上上的最大值为f（）==，解得a=1，‎ 综上所述，得 ‎（II）函数f（x）在（0，π）内有且仅有两个零点．证明如下：‎ 由（I）知，，从而有f（0）=﹣＜0，f（）=＞0，‎ 又函数在上图象是连续不断的，所以函数f（x）在（0，）内至少存在一个零点，‎ 又由（I）知f（x）在（0，）单调递增，故函数f（x）在（0，）内仅有一个零点．‎ 当x∈[，π]时，令g（x）=f′（x）=sinx+xcosx，由g（）=1＞0，g（π）=﹣π＜0，且g（x）在[，π]上的图象是连续不断的，故存在m∈（，π），使得g（m）=0．‎ 由g′（x）=2cosx﹣xsinx，知x∈（，π）时，有g′（x）＜0，从而g（x）在[，π]上单调递减．‎ 当x∈（，m），g（x）＞g（m）=0，即f′（x）＞0，从而f（x）在（，m）内单调递增 故当x∈（，m）时，f（x）＞f（）=＞0，从而（x）在（，m）内无零点；‎ 当x∈（m，π）时，有g（x）＜g（m）=0，即f′（x）＜0，从而f（x）在（，m）内单调递减．‎ 又f（m）＞0，f（π）＜0且f（x）在[m，π]上的图象是连续不断的，从而f（x）在[m，π]内有且仅有一个零点．‎ 综上所述，函数f（x）在（0，π）内有且仅有两个零点．‎ ‎　‎ 参与本试卷答题和审题的老师有：minqi5；吕静；qiss；xize；刘长柏；zlzhan；庞会丽；wfy814；caoqz；xintrl（排名不分先后）‎ ‎2017年2月3日