高中数学（人教版必修2）配套练习 第二章章末检测 7页

章末检测 一、选择题 1．下列推理错误的是 ( ) A．A∈l，A∈α，B∈l，B∈α⇒l⊂α B．A∈α，A∈β，B∈α，B∈β⇒α∩β＝AB C．l⊄α，A∈l⇒A∉α D．A∈l，l⊂α⇒A∈α 2．长方体 ABCD－A1B1C1D1 中，异面直线 AB，A1D1 所成的角等于 ( ) A．30° B．45° C．60° D．90° 3．下列命题正确的是 ( ) A．若两条直线和同一个平面所成的角相等，则这两条直线平行 B．若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行 C．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行 D．若两个平面都垂直于第三个平面，则这两个平面平行 4．在空间四边形 ABCD 的边 AB，BC，CD，DA 上分别取 E、F、G、H 四点，如果 EF， GH 交于一点 P，则 ( ) A．P 一定在直线 BD 上 B．P 一定在直线 AC 上 C．P 一定在直线 AC 或 BD 上 D．P 既不在直线 AC 上，也不在直线 BD 上 5．给定下列四个命题： ①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行； ②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直； ③垂直于同一直线的两条直线相互平行； ④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直． 其中，为真命题的是 ( ) A．①和② B．②和③ C．③和④ D．②和④ 6．已知平面α⊥平面β，α∩β＝l，点 A∈α，A∉l，直线 AB∥l，直线 AC⊥l，直线 m∥α，m∥β， 则下列四种位置关系中，不一定成立的是 ( ) A．AB∥m B．AC⊥m C．AB∥β D．AC⊥β 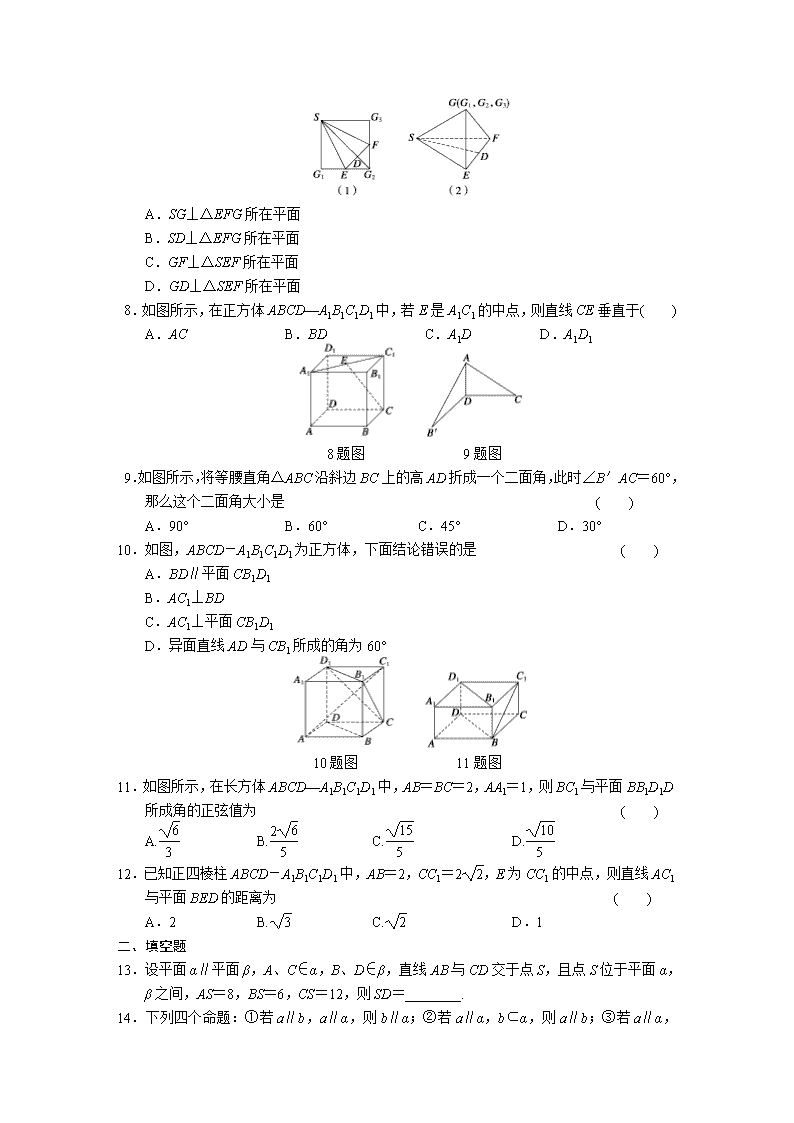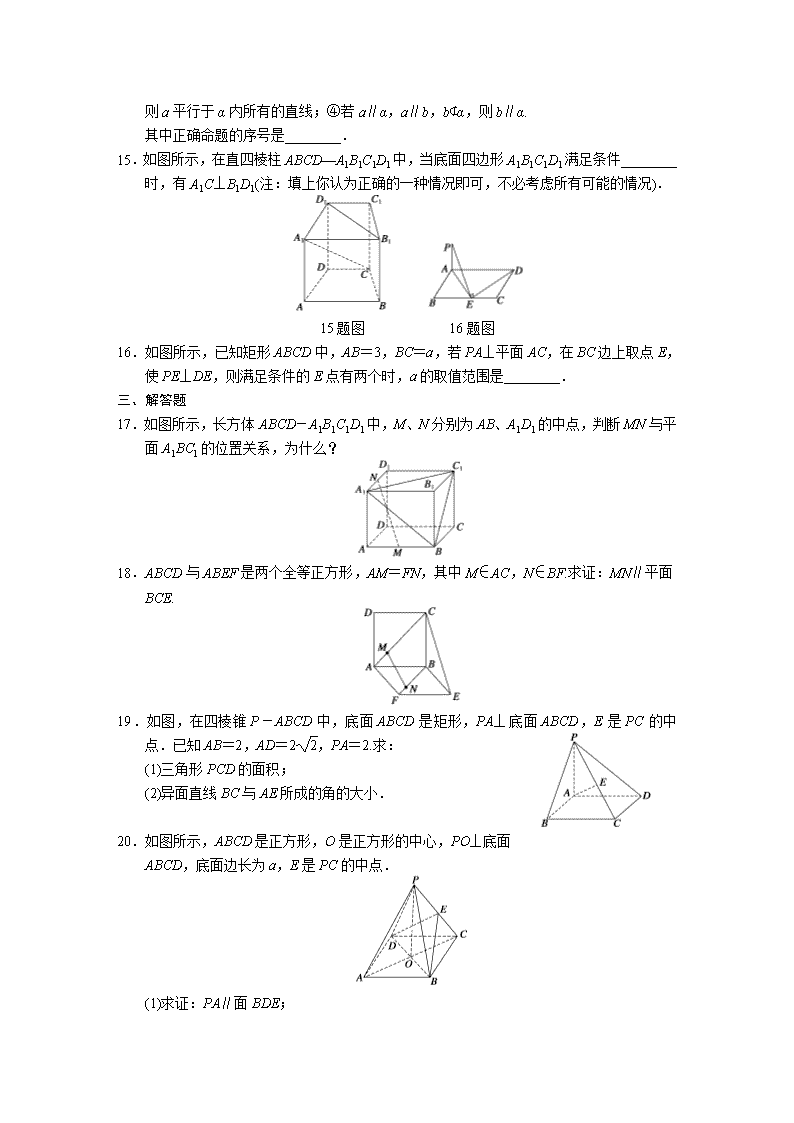7．如图(1)所示，在正方形 SG1G2G3 中，E，F 分别是 G1G2 及 G2G3 的中点，D 是 EF 的中点， 现在沿 SE，SF 及 EF 把这个正方形折成一个四面体，使 G1，G2，G3 三点重合，重合后 的点记为 G，如图(2)所示，那么，在四面体 S－EFG 中必有 ( ) A．SG⊥△EFG 所在平面 B．SD⊥△EFG 所在平面 C．GF⊥△SEF 所在平面 D．GD⊥△SEF 所在平面 8．如图所示，在正方体 ABCD—A1B1C1D1 中，若 E 是 A1C1 的中点，则直线 CE 垂直于( ) A．AC B．BD C．A1D D．A1D1 8 题图 9 题图 9．如图所示，将等腰直角△ABC 沿斜边 BC 上的高 AD 折成一个二面角，此时∠B′AC＝ 60°，那么这个二面角大小是 ( ) A．90° B．60° C．45° D．30° 10．如图，ABCD－A1B1C1D1 为正方体，下面结论错误的是 ( ) A．BD∥平面 CB1D1 B．AC1⊥BD C．AC1⊥平面 CB1D1 D．异面直线 AD 与 CB1 所成的角为 60° 10 题图 11 题图 11．如图所示，在长方体 ABCD—A1B1C1D1 中，AB＝BC＝2，AA1＝1，则 BC1 与平面 BB1D1D 所成角的正弦值为 ( ) A. 6 3 B.2 6 5 C. 15 5 D. 10 5 12．已知正四棱柱 ABCD－A1B1C1D1 中，AB＝2，CC1＝2 2，E 为 CC1 的中点，则直线 AC1 与平面 BED 的距离为 ( ) A．2 B. 3 C. 2 D．1 二、填空题 13．设平面α∥平面β，A、C∈α，B、D∈β，直线 AB 与 CD 交于点 S，且点 S 位于平面α，β 之间，AS＝8，BS＝6，CS＝12，则 SD＝________. 14．下列四个命题：①若 a∥b，a∥α，则 b∥α；②若 a∥α，b⊂α，则 a∥b；③若 a∥α，则 a 平行于α内所有的直线；④若 a∥α，a∥b，b⊄α，则 b∥α. 其中正确命题的序号是________． 15．如图所示，在直四棱柱 ABCD—A1B1C1D1 中，当底面四边形 A1B1C1D1 满足条件________ 时，有 A1C⊥B1D1(注：填上你认为正确的一种情况即可，不必考虑所有可能的情况)． 15 题图 16 题图 16．如图所示，已知矩形 ABCD 中，AB＝3，BC＝a，若 PA⊥平面 AC，在 BC 边上取点 E， 使 PE⊥DE，则满足条件的 E 点有两个时，a 的取值范围是________． 三、解答题 17．如图所示，长方体 ABCD－A1B1C1D1 中，M、N 分别为 AB、A1D1 的中点，判断 MN 与平 面 A1BC1 的位置关系，为什么？ 18．ABCD 与 ABEF 是两个全等正方形，AM＝FN，其中 M∈AC，N∈BF.求证：MN∥平面 BCE. 19．如图，在四棱锥 P－ABCD 中，底面 ABCD 是矩形，PA⊥底面 ABCD，E 是 PC 的中点．已 知 AB＝2，AD＝2 2，PA＝2.求： (1)三角形 PCD 的面积； (2)异面直线 BC 与 AE 所成的角的大小． 20．如图所示，ABCD 是正方形，O 是正方形的中心，PO⊥底面 ABCD，底面边长为 a，E 是 PC 的中点． (1)求证：PA∥面 BDE； (2)求证：平面 PAC⊥平面 BDE； (3)若二面角 E－BD－C 为 30°，求四棱锥 P－ABCD 的体积． 21．如图，四棱锥 P－ABCD 中，底面 ABCD 为菱形，PA⊥底面 ABCD， AC＝2 2，PA＝2，E 是 PC 上的一点，PE＝2EC. (1)证明：PC⊥平面 BED； (2)设二面角 A－PB－C 为 90°，求 PD 与平面 PBC 所成角的大小． 答案 1．C 2.D 3．C 4．B 5．D 6．D 7．A 8．B 9.A 10．D 11．D 12．D 13．9 14．④ 15．B1D1⊥A1C1(答案不唯一) 16．a>6 17．解 直线 MN∥平面 A1BC1，M 为 AB 的中点，证明如下： ∵MD/∈平面 A1BC1，ND/∈平面 A1BC1. ∴MN⊄平面 A1BC1. 如图，取 A1C1 的中点 O1，连接 NO1、BO1. ∵NO1 綊 1 2D1C1，MB 綊 1 2D1C1， ∴NO1 綊 MB. ∴四边形 NO1BM 为平行四边形． ∴MN∥BO1. 又∵BO1⊂平面 A1BC1， ∴MN∥平面 A1BC1. 18．证明 如图所示，连接 AN，延长交 BE 的延长线于 P，连接 CP. ∵BE∥AF， ∴FN NB ＝AN NP ， 由 AC＝BF，AM＝FN 得 MC＝NB. ∴FN NB ＝AM MC. ∴AM MC ＝AN NP ， ∴MN∥PC，又 PC⊂平面 BCE. ∴MN∥平面 BCE. 19．解 (1)因为 PA⊥底面 ABCD，所以 PA⊥CD. 又 AD⊥CD，所以 CD⊥平面 PAD，从而 CD⊥PD. 因为 PD＝ 22＋2 22＝2 3，CD＝2， 所以三角形 PCD 的面积为1 2 ×2×2 3＝2 3. (2)如图，取 PB 中点 F，连接 EF、AF，则 EF∥BC，从而∠AEF(或其补角)是异面直线 BC 与 AE 所成的角． 在△AEF 中，由 EF＝ 2，AF＝ 2，AE＝2 知△AEF 是等腰直角三角形， 所以∠AEF＝45°. 因此，异面直线 BC 与 AE 所成的角的大小是 45°. 20．(1)证明 连接 OE，如图所示． ∵O、E 分别为 AC、PC 的中点，∴OE∥PA. ∵OE⊂面 BDE，PA⊄面 BDE， ∴PA∥面 BDE. (2)证明 ∵PO⊥面 ABCD，∴PO⊥BD. 在正方形 ABCD 中，BD⊥AC， 又∵PO∩AC＝O， ∴BD⊥面 PAC. 又∵BD⊂面 BDE， ∴面 PAC⊥面 BDE. (3)解 取 OC 中点 F，连接 EF. ∵E 为 PC 中点， ∴EF 为△POC 的中位线，∴EF∥PO. 又∵PO⊥面 ABCD，∴EF⊥面 ABCD. ∵OF⊥BD，∴OE⊥BD. ∴∠EOF 为二面角 E－BD－C 的平面角，∴∠EOF＝30°. 在 Rt△OEF 中，OF＝1 2OC＝1 4AC＝ 2 4 a，∴EF＝OF·tan 30°＝ 6 12a， ∴OP＝2EF＝ 6 6 a. ∴VP－ABCD＝1 3 ×a2× 6 6 a＝ 6 18a3. 21．(1)证明 因为底面 ABCD 为菱形， 所以 BD⊥AC. 又 PA⊥底面 ABCD，所以 PC⊥BD. 如图，设 AC∩BD＝F，连接 EF. 因为 AC＝2 2，PA＝2，PE＝2EC， 故 PC＝2 3，EC＝2 3 3 ，FC＝ 2， 从而PC FC ＝ 6， AC EC ＝ 6. 因为PC FC ＝AC EC ，∠FCE＝∠PCA， 所以△FCE∽△PCA，∠FEC＝∠PAC＝90°.由此知 PC⊥EF. 因为 PC 与平面 BED 内两条相交直线 BD，EF 都垂直， 所以 PC⊥平面 BED. (2)解 在平面 PAB 内过点 A 作 AG⊥PB，G 为垂足． 因为二面角 A－PB－C 为 90°， 所以平面 PAB⊥平面 PBC. 又平面 PAB∩平面 PBC＝PB， 故 AG⊥平面 PBC，AG⊥BC. 因为 BC 与平面 PAB 内两条相交直线 PA，AG 都垂直， 故 BC⊥平面 PAB，于是 BC⊥AB， 所以底面 ABCD 为正方形，AD＝2， PD＝ PA2＋AD2＝2 2. 设 D 到平面 PBC 的距离为 d. 因为 AD∥BC，且 AD⊄平面 PBC，BC⊂平面 PBC， 故 AD∥平面 PBC，A、D 两点到平面 PBC 的距离相等，即 d＝AG＝ 2. 设 PD 与平面 PBC 所成的角为α， 则 sin α＝ d PD ＝1 2. 所以 PD 与平面 PBC 所成的角为 30°.