2021届高三入学调研试卷 文科数学（三） Word版含解析 13页

‎2021届高三入学调研试卷 文 科 数 学（三）‎ 注意事项：‎ ‎1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。‎ ‎2．选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。‎ ‎3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。‎ ‎4．考试结束后，请将本试题卷和答题卡一并上交。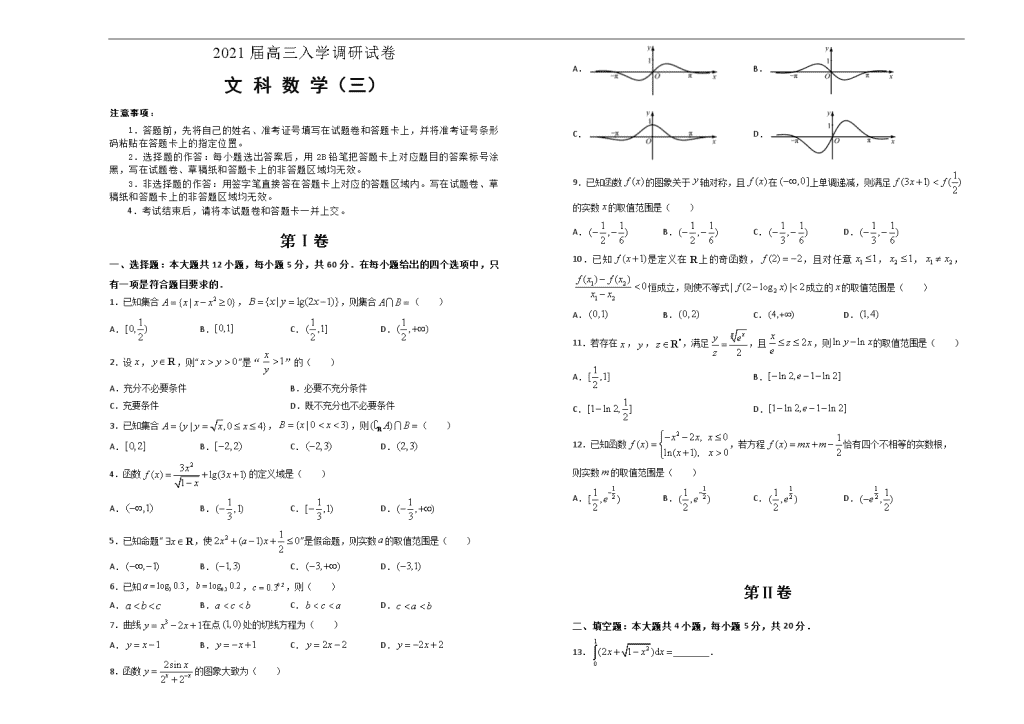‎ 第Ⅰ卷 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．已知集合，，则集合（ ）‎ A． B． C． D．‎ ‎2．设，，则“”是“”的（ ）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎3．已知集合，，则（ ）‎ A． B． C． D．‎ ‎4．函数的定义域是（ ）‎ A． B． C． D．‎ ‎5．已知命题“，使”是假命题，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎6．已知，，，则（ ）‎ A． B． C． D．‎ ‎7．曲线在点处的切线方程为（ ）‎ A． B． C． D．‎ ‎8．函数的图象大致为（ ）‎ A． B．‎ C． D．‎ ‎9．已知函数的图象关于轴对称，且在上单调递减，则满足的实数的取值范围是（ ）‎ A． B． C． D．‎ ‎10．已知是定义在上的奇函数，，且对任意，，，恒成立，则使不等式成立的的取值范围是（ ）‎ A． B． C． D．‎ ‎11．若存在，，，满足，且，则的取值范围是（ ）‎ A． B．‎ C． D．‎ ‎12．已知函数，若方程恰有四个不相等的实数根，‎ 则实数的取值范围是（ ）‎ A． B． C． D．‎ 第Ⅱ卷 二、填空题：本大题共4小题，每小题5分，共20分．‎ ‎13．________．‎ ‎14．已知命题“，”是假命题，则实数的取值范围是________．‎ ‎15．某食品的保鲜时间（单位：小时）与储藏温度（单位：）满足函数关系（为自然对数的底数，、为常数），若该食品在的保鲜时间是小时，在的保鲜时间是小时，则该食品在的保鲜时间是________小时．‎ ‎16．若，为自然数（），则下列不等式：①；②；③，其中一定成立的序号是________．‎ 三、解答题：本大题共6个大题，共70分．解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（10分）已知集合，．‎ ‎（1）当时，求；‎ ‎（2）若，求的取值范围．‎ ‎18．（12分）己知，．‎ ‎（1）若是真命题，求对应的取值范围；‎ ‎（2）若是的必要不充分条件，求的取值范围．‎ ‎19．（12分）已知函数．‎ ‎（1）若，求的值；‎ ‎（2）判断函数的奇偶性，并证明你的结论；‎ ‎（3）求不等式的解集．‎ ‎20．（12分）已知函数，曲线在点处的切线方程为．‎ ‎（1）求，的值；‎ ‎（2）证明：当且时，．‎ ‎21．（12分）定义域为的函数满足：，且对于任意实数，恒有，当时，．‎ ‎（1）求的值，并证明当时，；‎ ‎（2）判断函数在上的单调性并加以证明；‎ ‎（3）若不等式对任意恒成立，求实数的取值范围．‎ ‎22．（12分）已知函数．‎ ‎（1）当时，求证：；‎ ‎（2）讨论函数零点的个数．‎ ‎2021届高三入学调研试卷 文 科 数 学（三）答 案 第Ⅰ卷 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．【答案】C ‎【解析】因为，，所以．‎ ‎2．【答案】A ‎【解析】∵，∴，∴，即，‎ ‎∴“”是“”的充分条件；‎ 当，时，，但，所以“”不是“”的必要条件．‎ ‎3．【答案】D ‎【解析】∵，，‎ ‎∴，∴．‎ ‎4．【答案】B ‎【解析】函数的定义域是，解得，‎ 所以函数的定义域是．‎ ‎5．【答案】B ‎【解析】因为命题“，使”是假命题，‎ 所以，恒成立，‎ 所以，解得，‎ 故实数的取值范围是．‎ - 13 -‎ ‎6．【答案】B ‎【解析】，，，．‎ ‎7．【答案】A ‎【解析】验证知，点在曲线上，‎ 因为，，所以，得切线的斜率为，所以，‎ 所以曲线在点处的切线方程为，即．‎ ‎8．【答案】A ‎【解析】记为，，‎ ‎∴是奇函数，排除C；‎ 当时，，故B、D错误．‎ ‎9．【答案】B ‎【解析】由题意是偶函数，且在上单调递增，‎ ‎∴不等式可变为，‎ ‎∴，解得．‎ ‎10．【答案】D ‎【解析】因为函数的图象是由函数的图象向左平移个单位长度得到，‎ 是定义在上的奇函数，所以函数的图象的对称中心为点，‎ 因为对任意，，，恒成立，‎ 所以函数在上单调递减，所以函数在上单调递减，‎ 因为，所以，‎ 又，所以，即，‎ 所以即，所以，‎ 所以使不等式成立的的取值范围是．‎ ‎11．【答案】D ‎【解析】由题意，‎ - 13 -‎ ‎∵，∴，令，‎ 设，则，‎ ‎∴在上单调递减，在上单调递增，最小值为，‎ 由于，，‎ ‎∴的取值范围是．‎ ‎12．【答案】B ‎【解析】画出函数的图象如图中实线部分所示，‎ 方程恰有四个不相等的实数根，‎ 即函数与函数的图象有四个不同的交点，‎ 而是斜率为，过定点的直线，‎ 如图，当直线与相切时，设切点，‎ 又，可得，解得，斜率为，‎ 当直线过时，斜率为，‎ 所以当时，两函数的图象有个不同的交点．‎ 第Ⅱ卷 二、填空题：本大题共4小题，每小题5分，共20分．‎ - 13 -‎ ‎13．【答案】‎ ‎【解析】因，而，的几何意义为圆在第一象限所对应的面积为，‎ 故应填答案．‎ ‎14．【答案】‎ ‎【解析】若命题“，”是假命题，则“，”为真命题，则只需满足，解得．‎ ‎15．【答案】‎ ‎【解析】由题意可得，时，；时，，‎ 代入函数，可得，，即有，，‎ 则当时，．‎ ‎16．【答案】①③‎ ‎【解析】对于①，若成立．两边同时取对数可得，‎ 化简得，‎ 因为，则，，‎ 不等式两边同时除以可得，‎ 令，，则，‎ 当时，，所以，即在内单调递增，‎ 所以当时，，即，所以，故①正确；‎ 对于②，若，化简可得，‎ 令，，则，，‎ - 13 -‎ 由可知在内单调递增，‎ 而，，所以在内先负后正，‎ 因而在内先递减再递增，‎ 所以当时无法判断与的大小关系，故②错误；‎ 对于③，若，‎ 令，利用换底公式化简可得，，‎ 则，‎ 当时，，，‎ 所以，即，则在内单调递减，‎ 所以当时，，即，所以③正确，‎ 综上可知，正确的为①③．‎ 三、解答题：本大题共6个大题，共70分．解答应写出文字说明、证明过程或演算步骤．‎ ‎17．【答案】（1）；（2）．‎ ‎【解析】（1），时，，‎ ‎∴．‎ ‎（2）∵，‎ ‎∴当时，，即，符合题意；‎ 当时，或，解得或，‎ 综上，的取值范围为．‎ - 13 -‎ ‎18．【答案】（1）；（2）．‎ ‎【解析】（1）为真命题，即，解得．‎ ‎（2）根据（1）知：，，‎ 是的必要不充分条件，‎ 当时，，故满足，即；‎ 当时，，满足条件；‎ 当时，，故满足，即，‎ 综上所述，．‎ ‎19．【答案】（1）；（2）奇函数，证明见解析；（3）．‎ ‎【解析】（1）若，则，‎ 得，即，‎ 则，．‎ ‎（2）函数的定义域为，‎ ‎，即函数是奇函数．‎ ‎（3）由不等式，得，‎ ‎∵，∴在上是增函数，‎ 不等式等价为，即，即，得，‎ 即不等式的解集为．‎ ‎20．【答案】（1），；（2）证明见解析．‎ ‎【解析】（1），‎ 由于直线的斜率为，且过点，‎ - 13 -‎ 故，即，解得，．‎ ‎（2）由（1）知，所以，‎ 考虑函数，则，‎ 所以时，，而，‎ 故时，，可得；时，，可得，‎ 从而当，且时，．‎ ‎21．【答案】（1），证明见解析；（2）函数在上为减函数，证明见解析；（3）．‎ ‎【解析】（1）由已知，对于任意实数，恒有，‎ 令，，可得，‎ 因为当时，，所以，故．‎ 令，设，则，，‎ 因为，，所以．‎ ‎（2）设，则，‎ ‎，‎ 由（1）知，，所以，即，‎ 所以函数在上为减函数．‎ ‎（3）由，得，‎ 所以，‎ 即，‎ 上式等价于对任意恒成立，‎ 因为，所以，‎ - 13 -‎ 所以对任意恒成立，‎ 设，‎ ‎（时取等），‎ 所以，解得或，‎ 即实数的取值范围．‎ ‎22．【答案】（1）证明见解析；（2）见解析．‎ ‎【解析】（1）当时，，‎ 令，则，‎ 当时，；当时，；当时，，‎ 所以在上单调递减，在单调递增，‎ 所以是的极小值点，也是最小值点，‎ 即，‎ 故当时，成立．‎ ‎（2），由，得，‎ 当时，；当时，，‎ 所以在上单调递减，在单调递增，‎ 所以是函数得极小值点，也是最小值点，‎ 即．‎ 当，即时，没有零点；‎ 当，即时，只有一个零点；‎ 当，即时，‎ 因为，所以在上只有一个零点，‎ 由（1）得，令，则得，所以，‎ 于是在在上有一个零点，‎ 因此，当时，有两个零点．‎ 综上，时，没有零点；‎ 时，只有一个零点；‎ - 13 -‎ 时，有两个零点．‎ - 13 -‎