人教A版选修1-13-2立体几何中的向量方法第2课时（含答案） 7页

§3.2.2 空间角与距离的计算举例 【学情分析】： 教学对象是高二的学生，学生已经具备空间向量与立方体几何的相关知识,上次课已经学习了直线的 方向向量和平面的法向量，所以本节课是通过举例来求空间的距离和角。我们可以将空间中的有关距离和 角的问题，转化为空间向量的数量积来解决。 【教学目标】： （1）知识与技能：能用向量方法进行有关距离的计算；能用向量方法解决线线、线面与面面的夹角 的计算问题. （2）过程与方法：在解决问题中，通过数形结合的思想方法，加深对相关知识的理解。 （3）情感态度与价值观：体会把立方体几何几何转化为向量问题优势，培养探索精神。 【教学重点】： 将空间角与距离的计算转化为向量的夹角与模来计算. 【教学难点】： 将空间角与距离的计算转化为向量的夹角与模来计算. 【教学过程设计】： 教学环节 教学活动 设计意图 一、复习引 入 1． 两个向量的数量积如何运算？ 2． 向量的模与向量的数量积是什么关系？ 3． 向量的加法法则。 为探索新知识做准 备. 二、探究与 练习 一、用空间向量解决立体几何问题的“三步曲” 学生回顾用平面向量解决平面几何问题的“三步曲”，与老师共同得 出用空间向量解决立体几何问题的“三步曲”： （1）建立立体图形与空间向量的联系，用空间向量表示问题中涉及的 点、直线、平面，把立体几何问题转化为向量问题；（化为向量问题） （2）通过向量运算，研究点、直线、平面之间的位置关系以及它们之 间距离和夹角等问题；（进行向量运算） （3）把向量的运算结果“翻译”成相应的几何意义。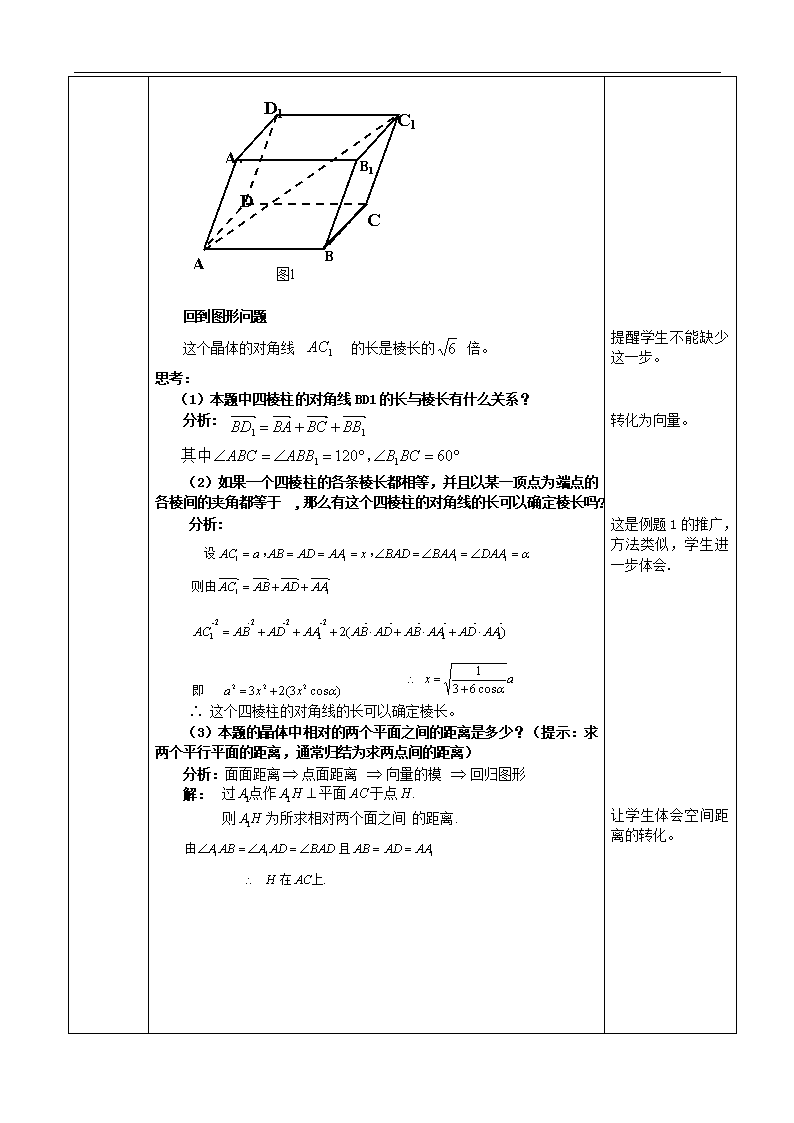（回到图形问题） 二、例题 例 1：如图 1：一个结晶体的形状为四棱柱，其中，以顶点 A 为端点 的三条棱长都相等，且它们彼此的夹角都是 60°，那么以这个顶点为端 点的晶体的对角线的长与棱长有什么关系？ 解：如图 1，设  6011 DAABAA 化为向量问题 依据向量的加法法则， 进行向量运算 )60cos60cos60(cos2111  6 6|| 1 AC 让学生通过回顾寻 找将立体几何问题 转化为向量问题的 步骤。 例 1 的图形比较规 范，容易把握，可 以让学生很好地体 会 向 量 解 题 的 优 势。  BADADAAAB ， 11 11 AAADABAC  2 1 2 1 )( AAADABAC  )(2 11 2 1 22 AAADAAABADABAAADAB  A1 B1 C1 D1 A B C D 图1 回到图形问题 这个晶体的对角线 的长是棱长的 6 倍。 思考： （1）本题中四棱柱的对角线 BD1 的长与棱长有什么关系？ 分析:  60 120 11 BCBABBABC ，其中 （2）如果一个四棱柱的各条棱长都相等，并且以某一顶点为端点的 各棱间的夹角都等于 , 那么有这个四棱柱的对角线的长可以确定棱长 吗? 分析:  1111 DAABAABADxAAADABaAC ，，设 11 AAADABAC 则由 )(2 11 2 1 222 1 AAADAAABADABAAADABAC  )cos3(23 222 xxa 即 ax cos63 1  ∴ 这个四棱柱的对角线的长可以确定棱长。 （3）本题的晶体中相对的两个平面之间的距离是多少？（提示：求 两个平行平面的距离，通常归结为求两点间的距离） 分析：面面距离 点面距离 向量的模 回归图形 解： 提醒学生不能缺少 这一步。 转化为向量。 这是例题 1 的推广， 方法类似，学生进 一步体会. 让学生体会空间距 离的转化。 1AC 11 BBBCBABD     . 11 HACHAA 于点平面点作过  . 1 的距离为所求相对两个面之间则 HA 111 AAADABBADADAABA  且由 . 上在 ACH 3 360cos211)( 22  ACBCABAC .160cos60cos)( 1111  BCAAABAABCABAAACAA 3 1 |||| cos 1 1 1    ACAA ACAAACA 3 6sin 1  ACA3 6sin 111  ACAAAHA ∴ 所求的距离是 。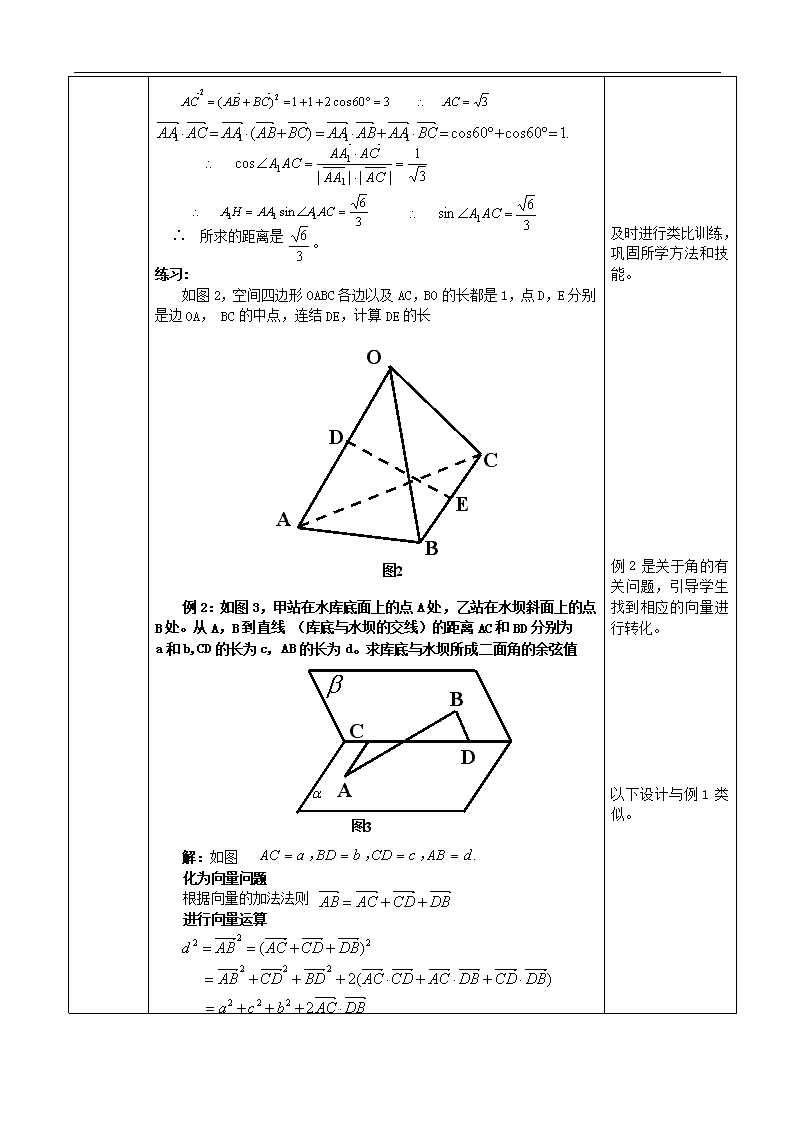 3 6 练习: 如图 2，空间四边形 OABC 各边以及 AC，BO 的长都是 1，点 D，E 分别 是边 OA， BC 的中点，连结 DE，计算 DE 的长 O A B C D E 图2 例 2：如图 3，甲站在水库底面上的点 A 处，乙站在水坝斜面上的点 B 处。从 A，B 到直线 （库底与水坝的交线）的距离 AC 和 BD 分别为 a 和 b,CD 的长为 c, AB 的长为 d。求库底与水坝所成二面角的余弦值 A B C D   图3 解：如图 化为向量问题 根据向量的加法法则 进行向量运算 及 时 进 行 类 比 训 练，巩固所学方法 和技能。 例 2 是关于角的有 关问题，引导学生 找到相应的向量进 行转化。 以下设计与例 1 类 似。 . dABcCDbBDaAC  ，，， DBCDACAB  222 )( DBCDACABd  )(2 222 DBCDDBACCDACBDCDAB  DBACbca  2222 DBCAbca  2222 22222 dcbaDBCA  设向量CA 与 DB 的夹角为 ， 就是库底与水坝所成的二面角。 因此 回到图形问题 库底与水坝所成二面角的余弦值为 思考： （1）本题中如果夹角 可以测出，而 AB 未知，其他条件不变，可 以计算出 AB 的长吗？ 分析： cos2222 abbca  )(2 222 DBCDDBACCDACBDCDAB  ∴ 可算出 AB 的长。 （2）如果已知一个四棱柱的各棱长和一条对角线的长，并且以同一 顶点为端点的各棱间的夹角都相等，那么可以确定各棱之间夹角的余弦 值吗？ 分析：如图，设以顶点 A 为端点的对角线长为 d，三条棱长分别为 a,b,c,各棱间夹角为 . A1 B1 C1 D1 A B CD .2cos 2222 ab dcba  .cos2 2222 dcbaab  .2 2222 ab dcba  22 )( DBCDACAB 由 2 1 2 1 2 )( CCACABCAd 则 cos)(2222 acbcabbca  )(2cos 2222 acbcab cbad    （3）如果已知一个四棱柱的各棱长都等 a，并且以某一顶点为端点 的各棱间的夹角都等于 ，那么可以确定这个四棱柱相邻两个夹角的余 弦值吗？ 分析：二面角 平面角 向量的夹角 回归图形 A1 B1 D1 A D E FB 解：如图，在平面 AB1 内过 A1 作 A1E⊥AB 于点 E，在平面 AC 内 作 CF⊥AB 于 F。  cos sin 1 aBFAEaCFEA  ，则  CFEAFCEA cos coscos 11 ，， |||| 1 1 CFEA CFEA  22 1 sin )()( a BFCBAEAA    22 22222 sin cos)cos(cos)cos(coscos a aaaa    cos1 cos  ∴可以确定这个四棱柱相邻两个夹角的余弦值。 练习： （1）如图 4，60°的二面角的棱上有 A、B 两点，直线 AC、BD 分别 在这个二面角的两个半平面内，且都垂直 AB，已知 AB＝4，AC＝6，BD＝ 8，求 CD 的长。 B 图4 A C D  2）三棱柱 ABC-A1B1C1 中，底面是边长为 2 的正三角形，∠A1AB＝ 45°，∠A1AC＝60°，求二面角 B-A A1-C 的平面角的余弦值。    C1 C A B C A1 B1 C1 图5 三、小结 1． 用空间向量解决立体几何问题的“三步曲”。 2． 面面距离  点面距离  向量的模  回归图形 二面角 平面角  向量的夹角 回归图形 反思归纳 四、作业 课本 P112 第 2、4 题。 练习与测试： （基础题） 1． 正四棱锥的侧棱长与底面边长都是 1，则侧棱与底面所成的角为（ ） A．75° B．60° C．45° D．30° 答：C。 2．如图，在棱长为 2 的正方体 1111 DCBAABCD  中，O 是底面 ABCD 的中心， E、F 分别是 1CC 、AD 的中点。那么异面直线 OE 和 1FD 所成的角的余弦值等 于（ ） A． 5 10 B． 5 15 C． 5 4 D． 3 2 答：B。 3，把正方形 ABCD 沿对角线 AC 折起,当以 A、B、C、D 四点为顶点的棱锥体积最大时，直线 BD 和平面 ABC 所成的角的大小为 ） A．90° B． 60° C，45° D． 30° 答：C。 4，已知 AB 是两条异面直线 ,AC BD 的公垂线段， 1, 10, 301AB AC BD CD    ，则 ,AC BD 所成 D1 C1 A1 B1 A B CD OF E · B1 P A CD A1 C1D1 B O H · 的角为 ． 答： 060 或 0120 。 （中等题） 5，一条线段夹在一个直二面角的两个面内，它和两个面所成的角都是 30°， 这条线段与这个二面角的棱所成的角为 。 答： 045 6，棱长为 4 的正方体 1 1 1 1ABCD A B C D 中， O 是正方形 1 1 1 1A B C D 的中心，点 P 在棱 1CC 上，且 1 4CC CP ． （Ⅰ）求直线 AP 与平面 1 1BCC B 所成的角的三角函数值； （Ⅱ）设 O 点在平面 1D AP 上的射影是 H ，求证： 1D H AP ． 解：（1）连 BP，则角 APB 为直线 AP 与平面 1 1BCC B 所成的角， 17 174 17 4tan  BP ABAPB （2） 02 1)( 111  APDBAPOHAPODAPOHODAPHD 所以 1D H AP