- 2.25 MB
- 2021-06-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
第1节 平面向量的概念及线性运算
最新考纲 1.了解向量的实际背景;2.理解平面向量的概念,理解两个向
量相等的含义;3.理解向量的几何表示;4.掌握向量加法、减法的运算,
并理解其几何意义;5.掌握向量数乘的运算及其几何意义,理解两个向量
共线的含义;6.了解向量线性运算的性质及其几何意义.
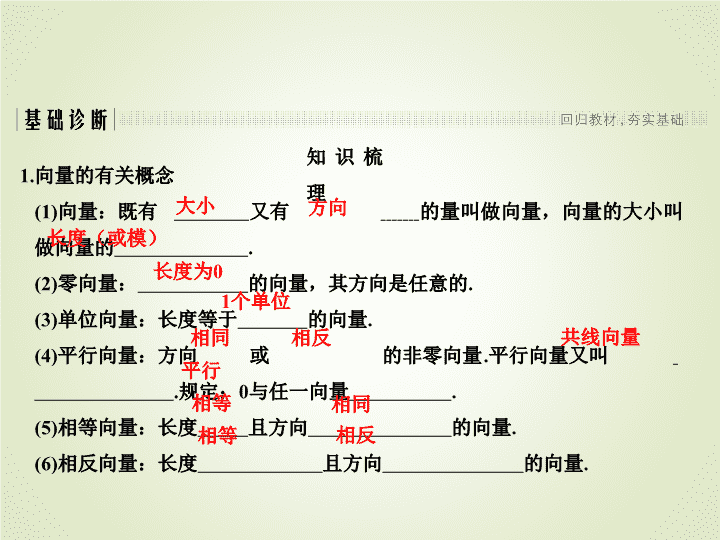
1.向量的有关概念
(1)向量:既有 又有 的量叫做向量,向量的大小叫
做向量的 .
(2)零向量: 的向量,其方向是任意的.
(3)单位向量:长度等于 的向量.
(4)平行向量:方向 或 的非零向量.平行向量又叫
.规定:0与任一向量 .
(5)相等向量:长度 且方向 的向量.
(6)相反向量:长度 且方向 的向量.
知 识 梳
理大小 方向
长度(或模)
长度为0
1个单位
相同 相反 共线向量
平行
相等 相同
相等 相反
2.向量的线性运算
向量运算 定 义 法则(或几何意义) 运算律
加法
求两个向量
和的运算
(1)交换律:a+b=________.
(2)结合律:
(a+b)+c=___________
减法
求a与b的相
反向量-b的
和的运算叫
做a与b的差
a-b=a+(-b)
b+a
a+(b+c)
3.共线向量定理
向量a(a≠0)与b共线的充要条件是存在唯一一个实数λ,使得
.
数乘
求实数λ与向量a
的积的运算
(1)|λa|=_______;
(2)当λ>0时,λa的方向
与a的方向______;当λ
<0时,λa的方向与a的
方向______;当λ=0时,
λa=_____
λ(μa)=_____;
(λ+μ)a=________;
λ(a+b)=_________
|λ||a|
相同
相反
0
λμa
λa+μa
λa+λb
b=λa
1.思考辨析(在括号内打“√”或“×”)
解析 (2)若b=0,则a与c不一定平行.
(3)共线向量所在的直线可以重合,也可以平行,则A,B,C,D四点不一
定在一条直线上.
答案 (1)√ (2)× (3)× (4)√
诊 断 自
测
答案 A
答案 A
答案 b-a -a-b
5.(2015·全国Ⅱ卷)设向量a,b不平行,向量λa+b与a+2b平行,则实数λ=
____________.
考点一 平面向量的概念
【例1】 给出下列四个命题:
解析 ①不正确.两个向量的长度相等,但它们的方向不一定相同.
③正确.∵a=b,∴a,b的长度相等且方向相同,又b=c,∴b,c的长度相
等且方向相同,∴a,c的长度相等且方向相同,故a=c.
④不正确.当a∥b且方向相反时,即使|a|=|b|,也不能得到a=b,故|a|=|b|
且a∥b不是a=b的充要条件,而是必要不充分条件.
综上所述,正确命题的序号是②③.
答案 A
【训练1】 下列命题中,正确的是________(填序号).
①有向线段就是向量,向量就是有向线段;
②向量a与向量b平行,则a与b的方向相同或相反;
③两个向量不能比较大小,但它们的模能比较大小.
解析 ①不正确,向量可以用有向线段表示,但向量不是有向线段,有
向线段也不是向量;
②不正确,若a与b中有一个为零向量,零向量的方向是不确定的,故两
向量方向不一定相同或相反;
③正确,向量既有大小,又有方向,不能比较大小;向量的模均为实数,
可以比较大小.
答案 ③
考点二 平面向量的线性运算
规律方法 1.解题的关键在于熟练地找出图形中的相等向量,并能熟练运
用相反向量将加减法相互转化.
2.用几个基本向量表示某个向量问题的基本技巧:(1)观察各向量的位置;
(2)寻找相应的三角形或多边形;(3)运用法则找关系;(4)化简结果.
考点三 共线向量定理及其应用
【例3】 设两个非零向量a与b不共线.
(2)解 ∵ka+b与a+kb共线,∴存在实数λ,
使ka+b=λ(a+kb),即ka+b=λa+λkb,
∴(k-λ)a=(λk-1)b.
∵a,b是不共线的两个非零向量,
∴k-λ=λk-1=0,∴k2-1=0,∴k=±1.
规律方法 1.证明三点共线问题,可用向量共线解决,但应注意向量共线
与三点共线的区别与联系,当两向量共线且有公共点时,才能得出三点共
线.
2.向量a,b共线是指存在不全为零的实数λ1,λ2,使λ1a+λ2b=0成立.
解析 由于c与d共线反向,则存在实数k使c=kd(k<0),
于是λa+b=k[a+(2λ-1)b].
整理得λa+b=ka+(2λk-k)b.
答案 B
相关文档
- 高中数学选修2-2教学课件1_5_1 曲2021-06-1646页
- 高中数学选修2-2教学课件第三章 1_2021-06-1644页
- 人教版高三数学总复习教学课件:6-32021-06-1669页
- 高中数学选修2-2教学课件第四章 3_2021-06-1617页
- 人教版高三数学总复习教学课件:5-32021-06-1664页
- 高中数学选修2-2教学课件第一章 2021-06-1632页
- 2018年高考数学考点突破教学课件:102021-06-1643页
- 2018年高考数学考点突破教学课件:2_2021-06-1629页
- 2018年高考数学考点突破教学课件:8_2021-06-1642页
- 2018年高考数学考点突破教学课件:4_2021-06-1642页