高中数学人教a版选修2-2（课时训练）：第三章 数系的扩充和复数的引入 章末复习 word版含答案 7页

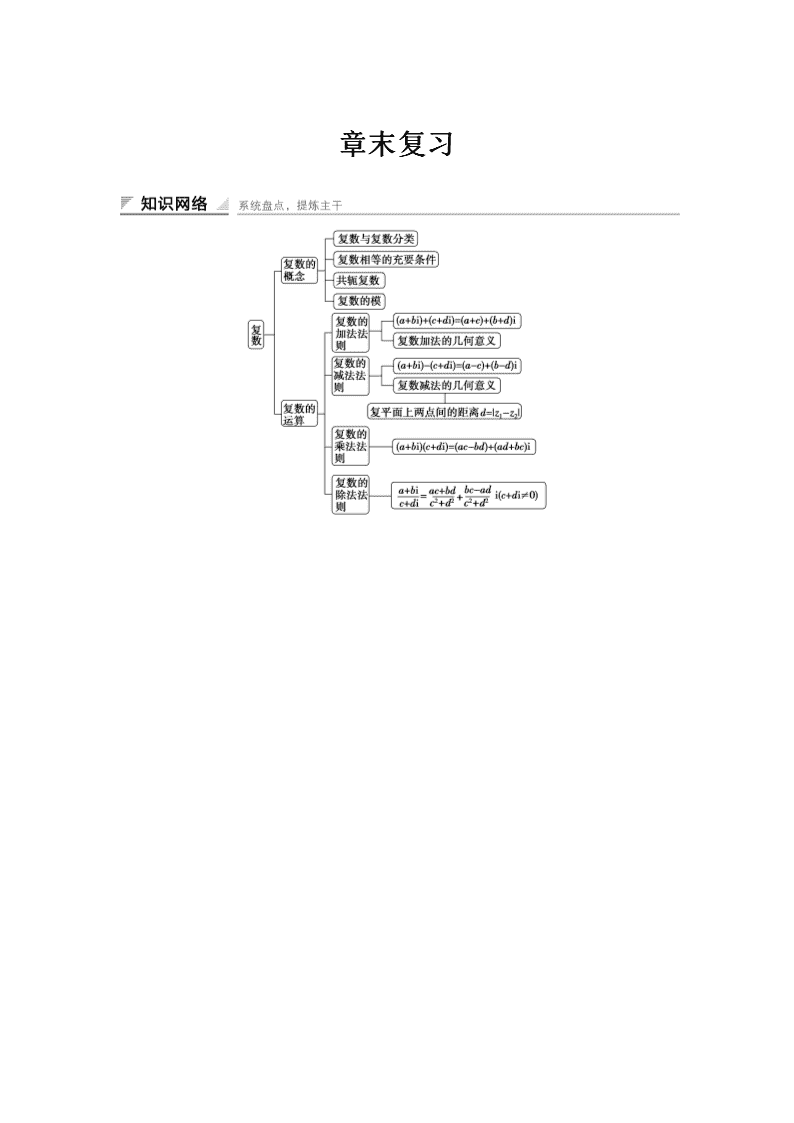
章末复习 1．复数的概念：(1)虚数单位 i；(2)复数的代数形式 z＝a＋bi(a，b∈R)；(3)复数的实部、虚 部、虚数与纯虚数． 2．复数集 复数 a＋bi a，b∈R 实数b＝0 有理数 整数 分数 无理数无限不循环小数 虚数b≠0 纯虚数a＝0 非纯虚数a≠0 3．复数的四则运算，若两个复数 z1＝a1＋b1i，z2＝a2＋b2i(a1，b1，a2，b2∈R) (1)加法：z1＋z2＝(a1＋a2)＋(b1＋b2)i； (2)减法：z1－z2＝(a1－a2)＋(b1－b2)i； (3)乘法：z1·z2＝(a1a2－b1b2)＋(a1b2＋a2b1)i； (4)除法：z1 z2 ＝a1a2＋b1b2＋a2b1－a1b2i a22＋b22 ＝a1a2＋b1b2 a22＋b22 ＋a2b1－a1b2 a22＋b22 i(z2≠0)； (5)实数四则运算的交换律、结合律、分配律都适合于复数的情况； (6)特殊复数的运算：in(n 为正整数)的周期性运算； (1±i)2＝±2i；若ω＝－1 2± 3 2 i，则ω3＝1,1＋ω＋ω2＝0. 4．共轭复数与复数的模 (1)若 z＝a＋bi，则 z ＝a－bi，z＋ z 为实数，z－ z 为纯虚数(b≠0)． (2)复数 z＝a＋bi 的模|z|＝ a2＋b2， 且 z· z ＝|z|2＝a2＋b2. 5．复数的几何形式 (1)用点 Z(a，b)表示复数 z＝a＋bi(a，b∈R)，用向量OZ→ 表示复数 z＝a＋bi(a，b∈R)，Z 称 为 z 在复平面上的对应点，复数与复平面上的点一一对应(坐标原点对应实数 0)． (2) 任何一个复数 z＝a＋bi 一一对应着复平面内一个点 Z(a，b)，也一一对应着一个从原点出发 的向量OZ→. 6．复数加、减法的几何意义 (1)复数加法的几何意义 若复数 z1、z2 对应的向量OZ1 → 、OZ2 → 不共线，则复数 z1＋z2 是以OZ1 → 、OZ2 → 为两邻边的平行四 边形的对角线OZ→所对应的复数． (2)复数减法的几何意义 复数 z1－z2 是连接向量OZ1 → 、OZ2 → 的终点，并指向 Z1 的向量所对应的复数． 题型一 分类讨论思想的应用 当复数的实部与虚部含有字母时，利用复数的有关概念进行分类讨论．分别确定什么情况 下是实数、虚数、纯虚数．当 x＋yi 没有说明 x，y∈R 时，也要分情况讨论． 例 1 已知复数 z＝a2－7a＋6 a2－1 ＋(a2－5a－6)i(a∈R)，试求实数 a 分别取什么值时，z 分别为(1) 实数；(2)虚数；(3)纯虚数． 解 (1)当 z 为实数时，则有 a2－5a－6＝0 a2－1≠0 ∴ a＝－1 或 a＝6 a≠±1 ，∴当 a＝6 时，z 为实数． (2)当 z 为虚数时， 则有 a2－5a－6≠0 a2－1≠0 ， ∴ a≠－1 且 a≠6 a≠±1 ，∴a≠±1 且 a≠6， 即当 a∈(－∞，－1)∪(－1,1)∪(1,6)∪(6，＋∞)时，z 为虚数． (3)当 z 为纯虚数时，则有 a2－5a－6≠0 a2－7a＋6 a2－1 ＝0， a2－1≠0 ∴ a≠－1 且 a≠6 a＝6 且 a≠±1 ∴不存在实数 a，使 z 为纯虚数． 跟踪演练 1 当实数 a 为何值时，z＝a2－2a＋(a2－3a＋2)i. (1)为实数； (2)为纯虚数； (3)对应的点在第一象限内； (4)复数 z 对应的点在直线 x－y＝0. 解 (1)z∈R⇔a2－3a＋2＝0，解得 a＝1 或 a＝2. (2)z 为纯虚数， a2－2a＝0， a2－3a＋2≠0， 即 a＝0 或 a＝2， a≠1 且 a≠2. 故 a＝0. (3)z 对应的点在第一象限，则 a2－2a＞0， a2－3a＋2＞0， ∴ a＜0，或 a＞2， a＜1，或 a＞2， ∴a＜0，或 a＞2. ∴a 的取值范围是(－∞，0)∪(2，＋∞)． (4)依题设(a2－2a)－(a2－3a＋2)＝0， ∴a＝2. 题型二 数形结合思想的应用 数形结合既是一种重要的数学思想，又是一种常用的数学方法．本章中，复数本身的几何 意义、复数的模以及复数加减法的几何意义都是数形结合思想的体现．它们得以相互转化．涉 及的主要问题有复数在复平面内对应点的位置、复数运算及模的最值问题等． 例 2 已知等腰梯形 OABC 的顶点 A、B 在复平面上对应的复数分别为 1＋2i，－2＋6i，OA ∥BC.求顶点 C 所对应的复数 z. 解 设 z＝x＋yi，x，y∈R，如图． ∵OA∥BC，|OC|＝|BA|， ∴kOA＝kBC，|zC|＝|zB－zA|， 即 2 1 ＝y－6 x＋2 ， x2＋y2＝ 32＋42， 解得 x1＝－5 y1＝0 或 x2＝－3 y2＝4 . ∵|OA|≠|BC|， ∴x2＝－3，y2＝4(舍去)， 故 z＝－5. 跟踪演练 2 已知复数 z1＝i(1－i)3. (1)求|z1|； (2)若|z|＝1，求|z－z1|的最大值． 解 (1)|z1|＝|i(1－i)3|＝|i|·|1－i|3＝2 2. (2)如图所示，由|z|＝1 可知，z 在复平面内对应的点的轨迹是半径为 1，圆心为 O(0,0)的圆， 而 z1 对应着坐标系中的点 Z1(2，－2)．所以|z－z1|的最大值可以看成是点 Z1(2，－2)到圆上 的点的距离的最大值．由图知|z－z1|max＝|z1|＋r(r 为圆半径)＝2 2＋1. 题型三 转化与化归思想的应用 在求复数时，常设复数 z＝x＋yi(x，y∈R)，把复数 z 满足的条件转化为实数 x，y 满足的 条件，即复数问题实数化的基本思想在本章中非常重要． 例 3 已知 z 是复数，z＋2i， z 2－i 均为实数，且(z＋ai)2 的对应点在第一象限，求实数 a 的取 值范围． 解 设 z＝x＋yi(x，y∈R)， 则 z＋2i＝x＋(y＋2)i 为实数，∴y＝－2. 又 z 2－i ＝x－2i 2－i ＝1 5(x－2i)(2＋i) ＝1 5(2x＋2)＋1 5(x－4)i 为实数， ∴x＝4.∴z＝4－2i，又∵(z＋ai)2＝(4－2i＋ai)2＝(12＋4a－a2)＋8(a－2)i 在第一象限． ∴ 12＋4a－a2>0 8a－2>0 ，解得 2