2020_2021学年新教材高中数学第7章三角函数7 10页

‎7.2　三角函数概念 ‎7.2.1　‎任意角的三角函数 学 习 目 标 核 心 素 养 ‎1．理解三角函数的定义，会使用定义求三角函数值．(重点、易错点)‎ ‎2．会判断给定角的三角函数值的符号．(重点)‎ ‎3．会利用三角函数线比较两个同名三角函数值的大小及表示角的范围．(难点)‎ 通过学习本节内容，提升学生的数学运算和数学抽象核心素养．‎ 在初中我们学习了锐角三角函数，那么锐角三角函数是如何定义的？若将锐角放入直角坐标系中，你能用角的终边上的点的坐标来表示锐角三角函数吗？若以单位圆的圆心O为原点，你能用角的终边与单位圆的交点来表示锐角三角函数吗？那么，角的概念推广之后，三角函数的概念又该怎样定义呢？‎ ‎1．任意角三角函数的定义 在平面直角坐标系中，设α的终边上异于原点的任意一点P的坐标为(x，y)，它与原点的距离是r(r＝>0)，那么 名称 定义 定义域 正弦 sin α＝ R 余弦 cos α＝ R 正切 tan α＝ sin α，cos α，tan α分别称为正弦函数、余弦函数、正切函数，统称为三角函数．‎ 思考1：对于确定的角α，sin α，cos α，tan α的值是否随P点在终边上的位置的改变而改变？‎ ‎[提示]　不会．因为三角函数值是比值，其大小与点P(x，y)在终边上的位置无关，只与角α的终边位置有关，即三角函数值的大小只与角有关．‎ 思考2：若P(x，y)为角α与单位圆的交点，sin α，cos α，tan α的值怎样表示？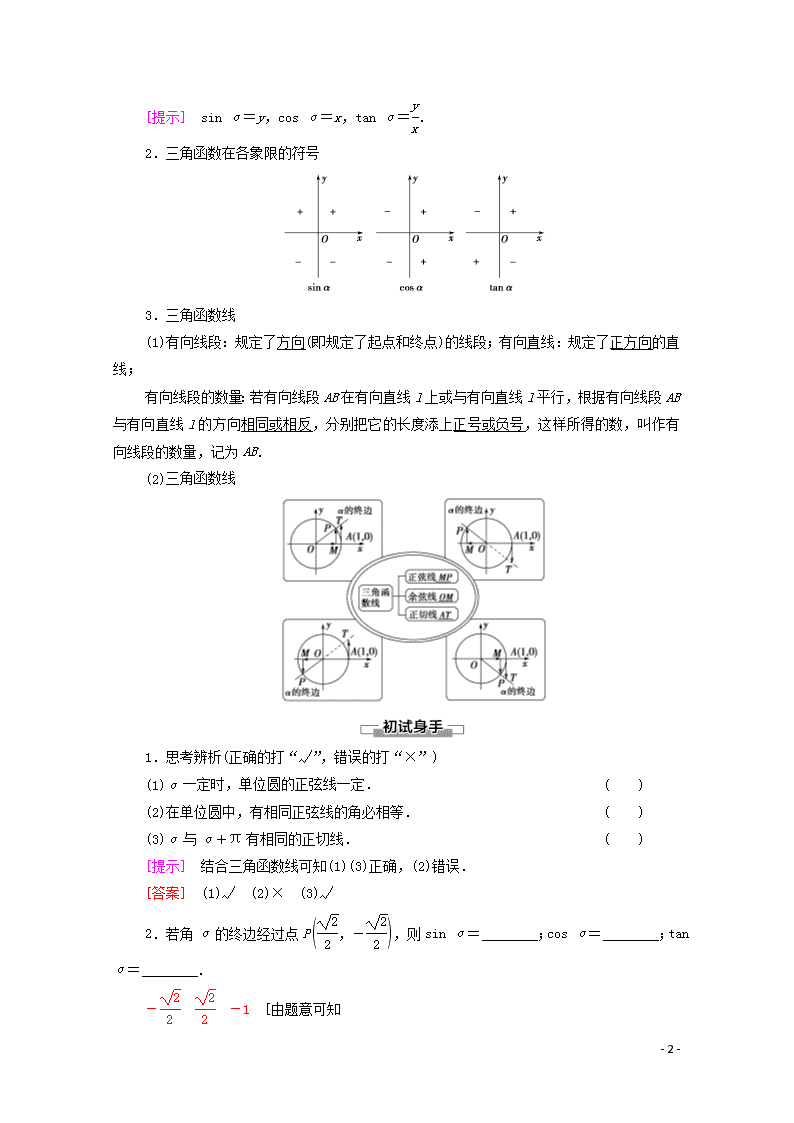‎ - 10 -‎ ‎[提示]　sin α＝y，cos α＝x，tan α＝．‎ ‎2．三角函数在各象限的符号 ‎3．三角函数线 ‎(1)有向线段：规定了方向(即规定了起点和终点)的线段；有向直线：规定了正方向的直线；‎ 有向线段的数量：若有向线段AB在有向直线l上或与有向直线l平行，根据有向线段AB与有向直线l的方向相同或相反，分别把它的长度添上正号或负号，这样所得的数，叫作有向线段的数量，记为AB．‎ ‎(2)三角函数线 ‎1．思考辨析(正确的打“√”，错误的打“×”)‎ ‎(1)α一定时，单位圆的正弦线一定． (　　)‎ ‎(2)在单位圆中，有相同正弦线的角必相等． (　　)‎ ‎(3)α与α＋π有相同的正切线． (　　)‎ ‎[提示]　结合三角函数线可知(1)(3)正确，(2)错误．‎ ‎[答案]　(1)√　(2)×　(3)√‎ ‎2．若角α的终边经过点P，则sin α＝　　　　；cos α＝　　　　；tan α＝　　　　．‎ ‎－　　－1　[由题意可知 - 10 -‎ ‎|OP|＝＝1，‎ ‎∴sin α＝＝－；cos α＝＝；‎ tan α＝＝－1．]‎ ‎3．(1)若α在第三象限，则sin αcos α　　　　0；(填“＞”或“＜”)‎ ‎(2)cos 3tan 4　　　　0．(填“>”或“<”)‎ ‎(1)＞　(2)＜　[(1)∵α在第三象限，‎ ‎∴sin α＜0，cos α＜0，∴sin αcos α＞0．‎ ‎(2)∵<3<π，π<4<，‎ ‎∴3是第二象限角，4是第三象限角．‎ ‎∴cos 3<0，tan 4>0．∴cos 3tan 4<0．]‎ 三角函数的定义及应用 ‎【例1】　(1)在平面直角坐标系中，角α的终边在直线y＝－2x上，求sin α，cos α，tan α的值．‎ ‎(2)当α＝－时，求sin α，cos α，tan α的值．‎ ‎[思路点拨]　(1)以α的终边分别在第二、四象限为依据，分别取特殊点求sin α，cos α，tan α的值．‎ ‎(2)先求出角α的终边与单位圆的交点坐标，再利用三角函数的定义求出sin α，cos α，tan α的值．‎ ‎[解]　(1)当α的终边在第二象限时，在α终边上取一点P(－1，2)，则r＝＝，‎ 所以sin α＝＝，cos α＝＝－，tan α＝＝－2．‎ 当α的终边在第四象限时，‎ 在α终边上取一点P′(1，－2)，‎ 则r＝＝，‎ - 10 -‎ 所以sin α＝＝－，cos α＝＝，tan α＝＝－2．‎ ‎(2) 当α＝－时，设α的终边与单位圆的交点坐标为P(x，y)，(x>0，y<0)‎ 根据直角三角形中锐角的邻边是斜边的一半，得x＝，由勾股定理得＋y2＝1，y<0，解得y＝－，‎ 所以P．因此sin α＝＝－，cos α＝＝，tan α＝＝－．‎ ‎1．已知角α终边上任意一点的坐标求三角函数值的方法 ‎(1)先利用直线与单位圆相交，求出交点坐标，然后再利用正、余弦函数的定义求出相应的三角函数值．‎ ‎(2)在α的终边上任选一点P(x，y)，设P到原点的距离为r(r>0)，则sin α＝，cos α＝．当已知α的终边上一点求α的三角函数值时，用该方法更方便．‎ ‎2．已知特殊角α，求三角函数值的方法 ‎(1)先设出角α的终边与单位圆交点坐标，由锐角三角形的定义结合勾股定理求出该点的坐标．‎ ‎(2)利用三角函数的定义，求出α的三角函数值．(此时P到原点的距离r＝1)‎ ‎3．当角α的终边上点的坐标以参数形式给出时，要根据问题的实际情况对参数进行分类讨论．‎ ‎1．已知角θ终边上一点P(x,3)(x≠0)，且cos θ＝x，求sin θ，tan θ．‎ ‎[解]　由题意知r＝，由三角函数定义得cos θ＝＝．‎ 又∵cos θ＝x，∴＝x．‎ ‎∵x≠0，∴x＝±1．‎ 当x＝1时，P(1,3)，‎ - 10 -‎ 此时sin θ＝＝，‎ tan θ＝＝3．‎ 当x＝－1时，P(－1,3)，‎ 此时sin θ＝＝，tan θ＝＝－3．‎ ‎2． 当α＝时，求sin α，cos α，tan α的值．‎ ‎[解]　当α＝时，设α的终边与单位圆的交点坐标为P(x，y)，(x<0，y<0)‎ 根据直角三角形中锐角的邻边是斜边的一半，得x＝－，由勾股定理得＋y2＝1，y<0，‎ 解得y＝－， 所以P．因此sin α＝＝－，cos α＝＝－，tan α＝＝．‎ 三角函数值的符号 ‎【例2】　(1)若α是第四象限角，则点P(cos α，tan α)在第　　　　象限．‎ ‎(2)判断下列各式的符号：‎ ‎①sin 183°；②tan ；③cos 5．‎ ‎[思路点拨]　先确定各角所在的象限，再判定各三角函数值的符号．‎ ‎(1)四　[∵α是第四象限角，‎ ‎∴cos α>0，tan α<0，‎ ‎∴点P(cos α，tan α)在第四象限．]‎ ‎(2)[解]　①∵180°<183°<270°，‎ ‎∴sin 183°<0；‎ ‎②∵<<2π，‎ ‎∴tan <0；‎ ‎③∵<5<2π，‎ - 10 -‎ ‎∴cos 5>0．‎ 对于已知角α，判断α的相应三角函数值的符号问题，常依据三角函数的定义，或利用口诀“一全正、二正弦、三正切、四余弦”来处理.‎ ‎3．判断下列式子的符号：‎ ‎(1)tan 108°·cos 305°；(2)；‎ ‎(3)tan 120°·sin 269°．‎ ‎[解]　(1)∵108°是第二象限角，∴tan 108°＜0．‎ ‎∵305°是第四象限角，∴cos 305°＞0．‎ 从而tan 108°·cos 305°＜0．‎ ‎(2)∵是第二象限角，是第四象限角，是第二象限角，‎ ‎∴cos ＜0，tan＜0，sin ＞0．‎ 从而＞0．‎ ‎(3)∵120°是第二象限角，∴tan 120°＜0，‎ ‎∵269°是第三象限角，∴sin 269°＜0．‎ 从而tan 120°·sin 269°＞0．‎ 应用三角函数线解三角不等式 ‎[探究问题]‎ ‎1．在单位圆中，满足sin α＝的正弦线有几条？试在图中明确．‎ ‎[提示]　两条，如图所示，MP1与NP2都等于．‎ - 10 -‎ ‎2．满足sin α≥的角的范围是多少？试在单位圆中给予明确．‎ ‎[提示]　如图中阴影部分所示，所求角α的取值范围为．‎ ‎【例3】　求函数f(x)＝＋ln的定义域．‎ ‎[思路点拨]　借助单位圆解不等式组便可．‎ ‎[解]　由题意，自变量x应满足不等式组 即 则不等式组的解的集合如图(阴影部分)所示，‎ ‎∴．‎ ‎1．利用三角函数线解三角不等式的方法 ‎(1)正弦、余弦型不等式的解法 对于sin x≥b，cos x≥a(sin x≤b，cos x≤a)，求解的关键是恰当地寻求点，只需作直线y＝b或x＝a与单位圆相交，连接原点与交点即得角的终边所在的位置，此时再根据方向即可确定相应的范围．‎ ‎(2)正切型不等式的解法 对于tan x≥c，取点(1，c)，连接该点和原点并反向延长，即得角的终边所在的位置，结合图象可确定相应的范围．‎ ‎2．利用三角函数线求函数的定义域 解答此类题目的关键在于借助于单位圆，作出等号成立时角α的三角函数线，然后运用运动的观点，找出符合条件的角的范围．在这个解题过程中实现了一个转化，即把代数问题几何化，体现了数形结合的思想．‎ - 10 -‎ ‎4．在单位圆中画出适合下列条件的角α的终边的范围，并由此写出角α的集合：‎ ‎(1)sin α≥；(2)cos α≤－．‎ ‎[解]　(1)作直线y＝交单位圆于A，B两点，连接OA，OB，则OA与OB围成的区域(图①阴影部分)即为角α的终边的范围，故满足条件的角α的集合为 ．‎ ‎(2)作直线x＝－交单位圆于C，D两点，连接OC，OD，则OC与OD围成的区域(图②阴影部分)即为角α终边的范围，故满足条件的角α的集合为 ．‎ ‎1．本节课的重点是三角函数的定义、三角函数值的符号以及三角函数线的画法、利用三角函数线解决问题，难点是三角函数的定义及应用，对三角函数线概念的理解．‎ ‎2．本节课要重点掌握的规律方法 ‎(1)三角函数的定义及应用；‎ ‎(2)三角函数值符号的判断；‎ ‎(3)三角函数线的画法及应用．‎ ‎3．本节课的易错点 ‎(1)已知α的终边所在的直线求α的三角函数值时，易忽视对α所在象限的讨论，造成漏解而发生解题错误．‎ ‎(2)画三角函数线的位置以及表示方法．‎ ‎1．若sin α＜0，tan α＞0，则α终边所在象限是(　　)‎ A．第一象限　　　　 B．第二象限 C．第三象限 D．第四象限 C　[由sin α＜0可知α的终边落在第三、四象限及y轴的负半轴上．‎ 由tan α＞0可知α的终边落在第一、三象限内．‎ - 10 -‎ 故同时满足sin α＜0，tan α＞0的角α为第三象限角．]‎ ‎2．(多选题)下列判断正确的是(　　)‎ A．当－<α<－时，sin α0‎ ABC　[对于A：如图，作出角α的正弦线MP，余弦线OM，正切线AT，‎ 观察可知sin α0，cos 3<0，tan 4>0，所以sin 2·cos 3·tan 4<0，所以D错误．故选ABC．]‎ ‎3．角α的终边经过点P(－b,4)且cos α＝－，则b的值为　　　　．‎ ‎3　[由三角函数的定义可知＝－，‎ ‎∴解得b＝3．]‎ ‎4．已知角α的终边在直线3x＋4y＝0上，求sin α，cos α，tan α的值．‎ - 10 -‎ ‎[解]　∵角α的终边在直线3x＋4y＝0上，∴在角α的终边上任取一点P(4t，－3t)(t≠0)，则x＝4t，y＝－3t，r＝＝＝5|t|，‎ 当t＞0时，r＝5t，sin α＝＝＝－，cos α＝＝＝，tan α＝＝＝－．‎ 当t＜0时，r＝－5t，sin α＝＝＝，cos α＝＝＝－，tan α＝＝＝－．‎ 综上可知，sin α＝－，cos α＝，tan α＝－；‎ 或sin α＝，cos α＝－，tan α＝－．‎ - 10 -‎